Condizioni esistenza della radice

Obiettivo (corso Analisi Matematica 1)

• Condizioni di esistenza della radice
• Disequazioni con la radice
• Esempi

Indice degli esempi

Trovare la condizione di esistenza di

1. $\sqrt{1-x^2}$ e di ${1\over \sqrt{1-x^2}}$
2. $\sqrt{-2x^2+3x+5}$, $\sqrt{|-2x^2+3x+5|}$, ${1\over \sqrt{-2x^2+3x+5}}$ e ${1\over \sqrt{|-2x^2+3x+5|}}$
3. $\sqrt{x^3-4x^2+3x}$
4. $\sqrt{{x^3-1\over x}}$
5. $\sqrt[3]{{x+2\over 7-x}}$ (nelle due convenzioni)
6. $(x+1)^2\leqslant (x-1)^2$

Radicali: Condizioni di esistenza

Dobbiamo distinguere due casi: le radici di ordine pari e le radici di ordine dispari.

Radice pari

Per le radici di ordini pari del tipo $$\sqrt[2n]{P(x)},\ n\in\mathbb{N}$$ la condizione di esistenza è $P(x) \geqslant 0$, con $P(x)$ una qualunque funzione (per ora un polinomio)

Radicali: Condizioni di esistenza

Radici dispari

Qual è il dominio di $\sqrt[3]{x}$?

Per la radici di ordine dispari (es. cubica) si hanno le seguenti convenzioni:

• se si assume di lavorare solo con valori reali, allora il dominio è $\mathbb{R}$;
• se si assume la convenzione della radice principale (coinvolgendo i numeri complessi, che introdurremo più avanti), allora il dominio è $\mathbb{R}^{+} = \left[0,\ +\infty\right)$.

Questo ultimo risultato è legato alla scrittura: $\sqrt[3]{x} = x^{{1\over3}} = e^{{1\over3} \ln{x}}$ (che vedremo in seguito)

Qui viene adottata la convenzione della radice principale (molti prof. utilizzano la prima convezione facendo la distinzione tra radici pari e radici dispari). Per rendersi conto dell'importanza della convenzione della radice principale: provate a disegnare con un programma di calcolo simbolico o numerico la funzione $\sqrt[3]{x}$ e capirete subito perché uso la seconda convenzione. Oppure chiedere di calcolare $\sqrt[3]{-27}$ o $\sqrt[3]{-\pi}$ e vedete cosa vi restituiscono.

Riassunto

Con la convezione della radice principale il dominio di $$\sqrt[n]{P(x)}$$ è sempre $$P(x)\geqslant 0$$ per ogni $n\in\mathbb{N}$

Radice a denominatore

Se la radice compare a denominatore, i.e. si ha la forma $$1\over\sqrt[n]{P(x)}$$ allora bisogna escludere il caso in cui $P(x)=0$, i.e. diventa $$P(x)>0$$

Esempi

Esempio 1

Trovare la condizione di esistenza di $${\sqrt{1-x^2}}$$ e di $${{1\over \sqrt{1-x^2}}}$$

Soluzione 1

Per le condizioni di esistenza di $$\sqrt{1-x^2}$$ dobbiamo imporre la condizione $$1-x^2\geqslant 0\;\implies\;x^2\leqslant 1$$ che ha soluzione $$-1\leqslant x\leqslant 1$$

Soluzione 2

Le condizioni di esistenza di $${1\over \sqrt{1-x^2}}$$ sono $$1-x^2> 0$$ dove lo zero viene escluso

Quindi sono $$-1< x < 1$$

Esempio 2

Trovare la condizione di esistenza di

1. $${\sqrt{-2x^2+3x+5}}$$
2. $${\sqrt{|-2x^2+3x+5|}}$$
3. $${{1\over \sqrt{-2x^2+3x+5}}}$$
4. $${{1\over \sqrt{|-2x^2+3x+5|}}}$$

Soluzione 1

La condizione di esistenza è: $$-2x^2+3x+5\geqslant0$$

Gli zeri di $-2x^2+3x+5\geqslant0$ sono: $$x_{1,2}={-3\pm\sqrt{9+40}\over -4}={-3\pm7\over -4}=\left\{-1,\ {5\over2}\right\}$$

Essendo $a<0$ la disequazione è positiva per valori interni, i.e.

$$ \mathcal{S} = \left\{-1\leqslant x \leqslant {5\over2}\right\} \quad {\text{ i.e. }} \left[-1,\ {5\over2}\right] \quad $$

Soluzione 2

Non ci sono limitazioni alla funzione $$\sqrt{|-2x^2+3x+5|}$$ e quindi la condizione di esistenza è $$\mathbb{R}$$

Infatti il valore assoluto produce sempre una risultato positivo

Soluzione 3

La condizione di esistenza è $$-2x^2+3x+5>0$$

Partendo dalla soluzione del punto 1, escludiamo gli zeri quindi si ha $$ \mathcal{S} = \left\{-1< x < {5\over2}\right\} $$

Soluzione 4

Le uniche limitazione alla funzione $${1\over \sqrt{|-2x^2+3x+5|}}$$ sono gli zeri del denominatore (in quanto il valore assoluto produce sempre un risultato positivo)

Quindi, la soluzione è $$ \mathcal{S} = \mathbb{R} \setminus\left\{-1,\ {5\over2}\right\} $$

Esempio 3

Trovare la condizione di esistenza di $${\sqrt{x^3-4x^2+3x}}$$

Soluzione

La condizione di esistenza è $$x^3-4x^2+3x\geqslant0$$

La disequazione può essere fattorizzata in $$x^3-4x^2+3x = x(x^2-4x+3)$$ da cui applico la regola dei segni

Segno di $x$: $x\geqslant0$

Per il segno di $x^2-4x+3$, calcolo gli zeri che sono $$x_{1,2}={4\pm\sqrt{16-12}\over 2}={4\pm2\over 2}=\left\{3,\ 1\right\}$$

Essendo $a>0$ la disequazione è positiva per valori esterni, i..e $$x^2-4x+3\geqslant 0\;\implies\; \left\{x\leqslant1\right\}\;\lor\;\left\{x\geqslant 3\right\}$$

Il segno del prodotto è riportato nell'immagine

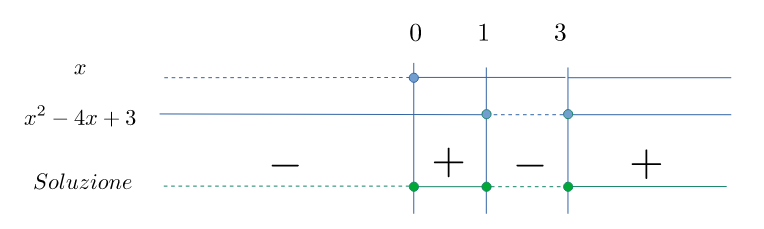
Dal momento che si devono scegliere i valori positivi, la soluzione è: $$ \mathcal{S} = \left\{0 \leqslant x\leqslant1\right\}\;\lor\;\left\{x\geqslant 3\right\} {\text{ i.e. }} \left[0,\ 1\right]\;\cup\;\left[3,\ +\infty\right) $$

Esempio 4

Trovare la condizione di esistenza di $${\sqrt{{x^3-1\over x}}}$$

Soluzione

Dobbiamo risolvere la disequazione $${x^3-1\over x}\geqslant0$$ applicando la regola dei segni

Segno del numeratore

Il numeratore si fattorizza come $$x^3-1=(x-1)(x^2+x+1)$$ dove si ha

• $x-1\geqslant 0 \;\implies\; x\geqslant 1$
• $x^2+x+1$ è sempre positivo ($\Delta < 0$)

Quindi il segno del denominatore è quello di $x-1$

Segno del denominatore

Dal denominatore dobbiamo escludere lo zero, i.e. si ha $$x>0$$

Segno della frazione e soluzione

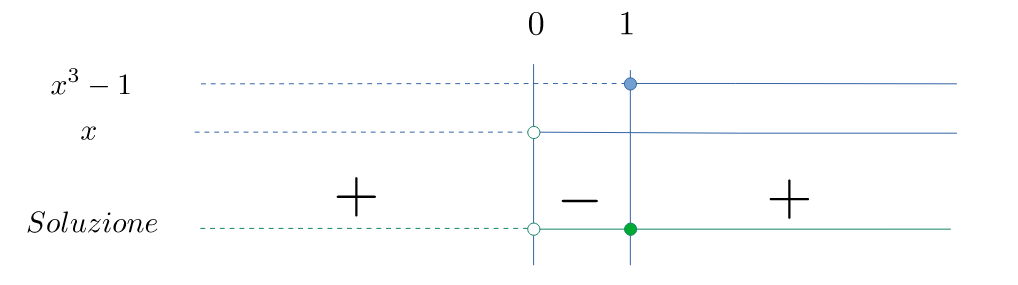
Vanno selezionati gli intervalli in cui è positiva o uguale a zero, quindi la soluzione è $$ \left\{x<0\right\}\;\lor\;\left\{x\geqslant 1\right\} {\text{ i.e. }} \left(-\infty,\ 0\right) \;\cup\; \left[1,\ +\infty\right) $$

Esempio 5

Trovare la condizione di esistenza di $${\sqrt[3]{{x+2\over 7-x}}}$$ nelle due convenzioni

Soluzione: convenzione dei reali

In questo caso la radice è di indice dispari quindi la condizione di esistenza è $$\mathbb{R}\setminus{7}$$

Soluzione: convenzione del ramo principale

Con la convenzione del ramo principale, tutte le radici devono avere argomento positivo o uguale a zero, i.e. $$ {x+2\over 7-x} \geqslant 0 $$ e quindi applico lo studio dei segni

Numeratore: $$x+2\geqslant 0\;\implies\; x \geqslant-2$$

Denominatore: $7-x>0 \;\implies\; -x>-7\;\implies\; x <7$

Il segno della frazione è riportato in figura.

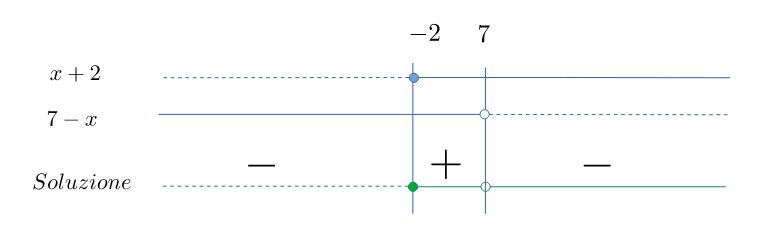
Viene richiesto di trovare tutti quei intervalli che danno come risultato un numero maggiore o uguale a 0, quindi $$ \mathcal{S} = \left\{-2\leqslant x < 7\right\} {\text{ i.e. }} \left[-2,\ 7\right) $$

Esempio 6

Trovare la condizione di esistenza di $${(x+1)^2\leqslant (x-1)^2}$$

Soluzione

Ricordiamo che

$$ \sqrt{x^2} = |x| $$

Applicando la radice ambo i membri, ricordando che la radice quadrata è una funzione strettamente crescente, si ha

$$ \sqrt{(x+1)^2}\leqslant \sqrt{(x-1)^2} \quad\implies\quad |x+1| \leqslant |x-1| $$

Per esplicitare i moduli dobbiamo distringuere i seguenti casi

1. $x\geqslant 1$
2. $-1< x < 1$
3. $x\leqslant -1$

Caso: 1

Se $x\geqslant 1$ allora si ha

$$|x+1| \leqslant |x-1| \quad\implies\quad x+1 \leqslant x-1 \quad\implies\quad 1 \leqslant -1$$

che non ha soluzione

Caso: 2

Se $-1< x < 1$ allora si ha

$$|x+1| \leqslant |x-1| \quad\implies\quad (x+1) \leqslant -(x-1) \quad\implies\quad 2x \leqslant 0$$

che ha soluzione $$ x \leqslant 0 $$

Questa soluzione va intersecata con il dominio di definizione della disequazione $-1< x < 1$ dando

$$ {-1< x \leqslant0} $$

Caso: 3

Se $x\leqslant -1$ allora si ha

$$|x+1| \leqslant |x-1| \quad\implies\quad -(x+1) \leqslant -(x-1) \quad\implies\quad -1 \leqslant 1$$

che ha soluzione per ogni $x$ del dominio di esistenza

Quindi intersecando le condizioni si ha

$$ {x\leqslant -1} $$

Soluzione finale

La soluzione finale si ottiene unendo le tre soluzione

• ${\emptyset}$
• ${-1< x \leqslant0}$
• ${x\leqslant -1}$

ottenendo

$$ {x\leqslant -1} \;\cup\; {-1< x \leqslant0} \;\implies\; {x \leqslant0} $$

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).