Disequazioni polinomiali con il valore assoluto

Obiettivo (corso Analisi Matematica 1)

• Disequazioni polinomiali con il valore assoluto
• Esempi

Indice degli esempi

Risolvere

1. $\left|{2x-6\over 3}\right|\geqslant 4$
2. $|x^2-8x+10|<3$
3. $\left|{2x+1\over x-3}\right|\geqslant 2$
4. $x^2+2|x|-3>0$
5. $1+|x|-|x^2-1|\leqslant 0$

Disequazioni polinomiali con il valore assoluto

L'idea è di trovare il campo di validità del valore assoluto

$$ |x|={\begin{cases}x,&{\text{se }}x\geqslant 0\\-x,&{\text{se }}x<0\end{cases}} $$

Esempi

Esempio 1

Risolvere $${\left|{2x-6\over 3}\right|\geqslant 4}$$

Soluzione

Con il cambio di variabile $$t={2x-6\over 3}$$ si ha $$|t|\geqslant 4\quad\quad \implies {t\leqslant -4}\;\lor\;{t\geqslant 4}$$

Quindi dobbiamo risolvere le seguenti due disequazioni:

• $t\leqslant -4 \implies {2x-6\over 3}\leqslant -4$
• $t\geqslant 4 \implies {2x-6\over 3}\geqslant 4$

La prima ha soluzione $${2x-6\over 3}\leqslant -4\;\implies\;2x\leqslant-12+6\;\implies x\leqslant-3$$

La seconda ha soluzione $${2x-6\over 3}\geqslant 4\;\implies\;2x\geqslant 12+6\;\implies x\geqslant 9$$

La soluzione finale si ottiene unendo le due soluzione, i.e $$\left\{x\leqslant-3\right\}\;\lor\;\left\{x\geqslant 9\right\}$$ che in termini di intervalli corrisponde a $$\left(-\infty,\ -3\right]\;\cup\;\left[9,\ +\infty\right)$$

Esempio 2

Risolvere $${|x^2-8x+10|<3}$$

Soluzione

La disequazione può essere riscritta come $$-3 < x^2-8x+10 < 3$$

Quindi si devono risolvere le seguenti due disequazioni

• $x^2-8x+10 > -3$
• $x^2-8x+10 < 3$

e intersecare successivamente le soluzioni

La prima disequazione diventa $$x^2-8x+10 > -3\;\implies\;x^2-8x+13>0$$

Gli zeri sono $$x_{1,2}={8\pm\sqrt{64-52}\over 2}={8\pm\sqrt{12}\over 2}=4\pm\sqrt{3}$$

Essendo $a=1>0$ la disequazione è verificata per valori esterni alle radici i.e. $${x<4-\sqrt{3}\} \;\lor\; \{x>4+\sqrt{3}}$$

La seconda disequazione diventa $$x^2-8x+10 < 3\;\implies\;x^2-8x+7<0$$

Gli zeri sono $$x_{1,2}={8\pm\sqrt{64-28}\over 2}={8\pm\sqrt{36}\over 2}=4\pm3=\left\{7,\ 1\right\}$$

Essendo $a=1>0$ la disequazione è verificata per valori interni alle radici i.e. $${1 < x<7}$$

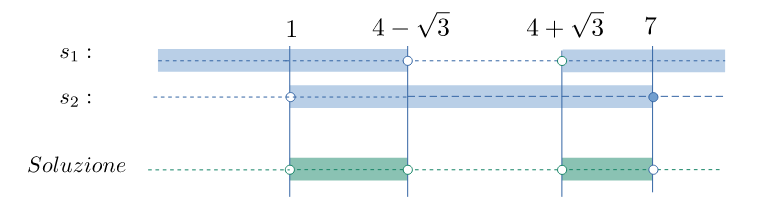
La soluzione finale si ottiene intersecando le due soluzioni, i.e. $$ \left\{1 < x < 4-\sqrt{3}\right\} \; \lor\; \left\{4+\sqrt{3}<x<7\right\} $$ che in termini di intervalli corrisponde a $$ \left(1,\ 4-\sqrt{3}\right)\;\cup\;\left(4+\sqrt{3},\ 7\right) $$

Esempio 3

Risolvere $${\left|{2x+1\over x-3}\right|\geqslant 2}$$

Soluzione

La disequazione corrisponde alle seguenti due disequazioni

• ${2x+1\over x-3}\geqslant 2$, oppure
• ${2x+1\over x-3}\leqslant -2$

La prima disequazione può essere riscritta come $$ {2x+1\over x-3}-2\geqslant 0\;\implies\;{2x+1-2(x-3)\over x-3}\geqslant 0\;\implies\;{5\over x-3}\geqslant 0 $$ che è positiva per $$x>3$$

La seconda disequazione può essere riscritta come $$ {2x+1\over x-3}+2\leqslant 0\;\implies\;{2x+1+2(x-3)\over x-3}\leqslant 0\;\implies\;{4x-5\over x-3}\leqslant 0 $$

Applichiamo lo studio del segno della frazione.

Il numeratore è positivo o uguale a zero se $4x-5\geqslant 0\;\implies\; x\geqslant{5\over4}$

Il denominatore è positivo se $x-3>0\;\implies\; x>3$

Applicando la regola dei segni, la disequazione è negativa (soluzione richiesta) se $$ {5\over4} \leqslant x < 3 $$

Esempio 4

Risolvere $${x^2+2|x|-3>0}$$

Soluzione

Per risolvere questo tipo di disequazioni dobbiamo esplicitare il $|x|$ in modo tale poter semplificarla.

Ricordando la definizione di $|x|$ si hanno le seguenti due casistiche:

1. $x\geqslant0$
2. $x<0$

Se $x\geqslant0$ si ha $$\begin{cases} x\geqslant 0\\ x^2+2x-3>0 \end{cases}$$

Se $x < 0$ si ha $$\begin{cases} x < 0 \\ x^2-2x-3 > 0 \end{cases}$$

Soluzione di 1

Gli zeri di $$x^2+2x-3$$ sono $$x_{1,2}={-2\pm\sqrt{4+12}\over2}={-2\pm4\over2}=\left\{1,\ -3\right\}$$

Essendo $a>0$, la disequazione è positiva per valori esterni, $$x^2+2x-3>0\;\implies\; \left\{x<-3\right\}\;\lor\;\left\{x>1\right\}$$

Intersencando le soluzioni

• ${x\geqslant 0}$
• $\left\{x<-3\right\}\;\lor\;\left\{x>1\right\}$

si ha

$$ \mathcal{S}_1=\left\{x>1\right\} $$

Soluzione di 2

Gli zeri di $$x^2-2x-3$$ sono $$x_{1,2}={2\pm\sqrt{4+12}\over2}={2\pm4\over2}=\left\{3,\ -1\right\}$$

Essendo $a>0$, la disequazione è positiva per valori esterni, $$x^2-2x-3>0\;\implies\; \left\{x<-1\right\}\;\lor\;\left\{x>3\right\}$$

Intersencando le soluzioni

• ${x< 0}$
• $\left\{x<-1\right\}\;\lor\;\left\{x>3\right\}$

si ha

$$ \mathcal{S}_1=\left\{x<-1\right\} $$

Soluzione finale

La soluzione finale è l'unione delle due, i.e. $$ \mathcal{S} = \left\{x<-1\right\}\;\lor\;\left\{x>1\right\} $$

Nota: Si poteva studiare solamente il caso $x\geqslant0$ osservando che la disequazione è una funzione pari e quindi concludere per simmetria la soluzione.

Esempio 5

Risolvere $${1+|x|-|x^2-1|\leqslant 0}$$

Soluzione

Per risolvere questa disequazioni dobbiamo esplicitare i diversi moduli.

Notiamo che la disequazione è pari (quindi la studiamo solamente per $x\geqslant 0$)

Ricordando la definizione modulo per $x$ e $x^2-1$ si hanno le seguenti tre casistiche:

1. $x\geqslant 1$ dove $|x^2-1|=x^2-1$ e $|x|=x$
2. $0\leqslant x<1$ dove $|x^2-1|=-(x^2-1)$ e $|x|=x$

Soluzione di 1

Se $x\geqslant 1$ dove $|x^2-1|=x^2-1$ e $|x|=x$

$$1+|x|-|x^2-1|\leqslant 0 \;\implies\; 1+x-(x^2-1) \leqslant 0 \;\implies\;-x^2+x+2\leqslant 0$$

Ora si ha

$$ -x^2+x+2= 0 \;\implies\; x_{1,2}={-1\pm\sqrt{1+8}\over -2} = {-1\pm3\over -2} = {-1,\ 2} $$

$$ -x^2+x+2\leqslant 0 \;\implies\; {x\leqslant -1} \;\lor\; {x\geqslant 2} $$

Quindi la soluzione (intersezione) è:

$$ {x\geqslant 2} $$

Soluzione di 2

Se $0\leqslant x<1$ dove $|x^2-1|=-(x^2-1)$ e $|x|=x$ allora

$$1+|x|-|x^2-1|\leqslant 0 \;\implies\; 1+x+(x^2-1) \leqslant 0 \;\implies\;x^2+x\leqslant 0$$

Ora si ha

$$ x^2+x\leqslant 0 \;\implies\; x(x+1)\leqslant 0 \;\implies\; {-1\leqslant x \leqslant0} $$

Quindi la soluzione (intersezione) è:

$$ x={0} $$

Soluzione finale

La soluzione finale si ottiene unendo le due soluzioni

• ${x\geqslant 2}$
• $x={0}$

e considerando la parità, da cui si ha la soluzione finale

$$ \mathcal{S} = {x\leqslant -2} \;\cup\; {0} \;\cup\; {x\geqslant 2} $$

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).