Disequazioni con rapporto tra polinomi
Obiettivo (corso Analisi Matematica 1)
- Disequazione data dal rapporto tra polinomi
- Studio del segno del numeratore
- Studio del segno del denominatore
Indice degli esempi
Risolvere
- ${x+2\over x^2-5x+4}\geqslant0$
- ${6\over 2x-1}>{5\over x-2}$
- ${x^2-5x+4\over x^2+2x+1}\geqslant 0$
- ${x^2-5x+4\over x^2+x+1}\leqslant 0$
- ${x^2-5x+4\over 9-4x^2}\geqslant 0$
- ${x\cdot (x^2-4)\over (x^2-3)(x^2-8x+12)}\leqslant 0$
Disequazione rapporto tra polinomi
Condizioni di esistenza
In questa lezione studieremo disequazioni del tipo $${{N(x)\over D(x)}\lesseqgtr 0}$$ ovvero rapporto tra due polinomi ($N(x)$ il numeratore e $D(x)$ il denominatore)
Allora studio del segno della disequazione va aggiunta la condizione di esistenza $D(x)\ne0$, i.e. vanno esclusi gli zeri del denominatori (chiamati anche poli)
Esempi
Esempio 1
Risolvere $${{x+2\over x^2-5x+4}\geqslant0}$$
Soluzione
Segno del numeratore
$$x+2\geqslant0 \;\implies\; x\geqslant-2$$
Segno del denominatore
Zeri: $$x^2-5x+4=0\;\implies\;x_{1,2}={5\pm\sqrt{25-16}\over 2}={5\pm3\over 2}=\left\{4,\ 1\right\}$$
Il denominatore può essere fattorizzato in $$1\cdot (x-1)\cdot (x-4)$$
Segno del denominatore ($a=1$ quindi è positivo per valore esterni): $$x^2-5x+4>0\;\implies\;\left\{x<1\right\} \;\lor\; \left\{x>4\right\}$$
Segno della frazione
Dobbiamo combinare il segno del numeratore con il segno del denominare escludendo gli zeri del denominatore (poli)
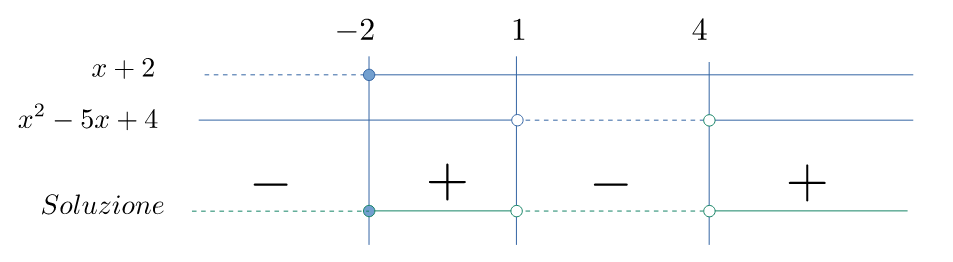
Dalla figura si ha la soluzione: $$\mathcal{S}=\left\{-2\leqslant x <1\right\} \;\lor\;\left\{x >4\right\}$$ corrispondenti agli intervalli $$\left[-2, \ 1\right)\cup \left(4,\ +\infty\right)$$
Esempio 2
Risolvere $${{6\over 2x-1}>{5\over x-2}}$$
Soluzione
Bisogna portare la disequazione in forma standard, ovvero deve essere della forma $${N(x)\over D(x)}\lesseqgtr 0$$ dove il termine di destra deve essere $0$.
Questo è essenziale per poter applicare la legge dell'annullamento del prodotto e la regola dei segni.
La disequazione può essere riscritta come $$\begin{gathered} {6(x-2)-5(2x-1)\over(2x-1)(x-2)}>0\\ {-4x-7\over(2x-1)(x-2)}>0\\ {\text{(moltiplico per $-1$) per semplificarla ulteriormente}}\\ {4x+7\over(2x-1)(x-2)}<0\\ \end{gathered}$$
Segno del numeratore
Nello studio del segno del numeratore evitiamo di studiare l'uguaglianza in quanto la disequazione di partenza non lo possiede.
$$4x+7>0 \;\implies\; x>-{7\over 4}$$
Segno del denominatore
Studio dei singoli fattori:
- $2x-1>0\;\implies\; x>{1\over2}$
- $x-2>0\;\implies\; x>2$
Segno della frazione
Riportiamo nella figura i segni dei 3 fattori
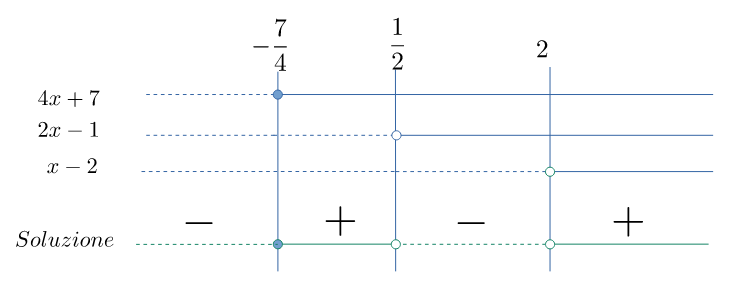
Va scelta la soluzione negativa (dall'ultima disequazione semplificata).
Esempio 2
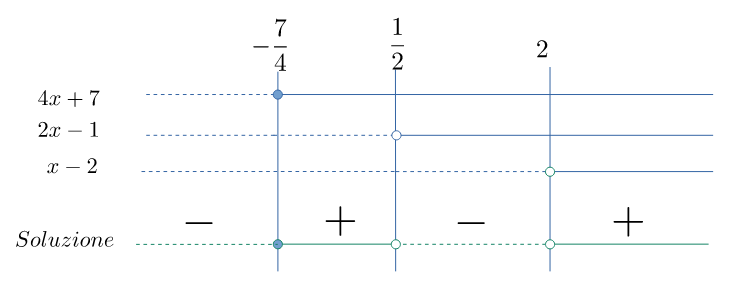
Dalla figura si ha la soluzione (negativa): $$\mathcal{S}=\left\{x \leqslant -{7\over4}\right\} \;\lor\; \left\{{1\over2}< x <2\right\} $$ corrispondenti agli intervalli $$\left(-\infty, \ -{7\over4}\right]\cup \left({1\over2},\ 2\right)$$
Esempio 3
Risolvere $${{x^2-5x+4\over x^2+2x+1}\geqslant 0}$$
Soluzione
Studio del segno del numeratore
Zeri: $$x^2-5x+4=0\;\implies\;x_{1,2}={5\pm\sqrt{25-16}\over 2}={5\pm3\over 2}=\left\{4,\ 1\right\}$$
Segno del numeratore ($a=1$ quindi è positivo o uguale a zero per valore esterni): $$x^2-5x+4\geqslant0\;\implies\;\left\{x\leqslant1\right\} \;\lor\; \left\{x\geqslant4\right\}$$
Studio del segno del denominatore
Il denominatore è il prodotto notevole (quadrato di un binomio): $$(x+1)^2$$
Quindi è sempre positivo tranne quando vale zero, che deve essere escluso perché al denominatore non posso dividere per zero.
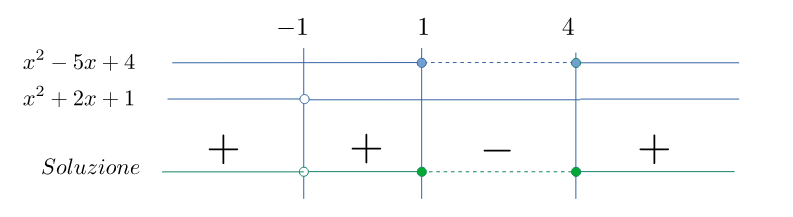
Soluzione finale
Il segno della frazione è dato dal segno del numeratore (il denominatore è sempre positivo). escluso il punto $1$ come da grafico.
Soluzione: $$\mathcal{S}=\left\{x<-1\right\}\;\lor\;\left\{-1<x\leqslant1\right\}\;\lor\;\left\{x\geqslant4\right\}$$
In termini di intervalli: $$(-∞, -1)\cup (-1, 1] \cup [4, ∞)$$
Esempio 4
Risolvere $${{x^2-5x+4\over x^2+x+1}\leqslant 0}$$
Soluzione
Studio del segno del numeratore
Zeri: $$x^2-5x+4=0\;\implies\;x_{1,2}={5\pm\sqrt{25-16}\over 2}={5\pm3\over 2}=\left\{4,\ 1\right\}$$
Segno del numeratore ($a=1$ quindi è positivo o uguale a zero per valore esterni): $$x^2-5x+4\geqslant0\;\implies\;\left\{x\leqslant1\right\} \;\lor\; \left\{x\geqslant4\right\}$$
Studio del segno del denominatore
Da $$\Delta=1-4=-3<0$$ si ha che il denominatore è irriducibile, infatti è la somma di due quadrati $$ x^2+x+1=\left(x^2+x+{1\over 4}\right)+\left(1-{1\over 4}\right)=\left(x+{1\over2}\right)^2+ \left({\sqrt{3}\over2}\right)^2 $$ e risulta pertanto sempre positivo.
Esempio 4
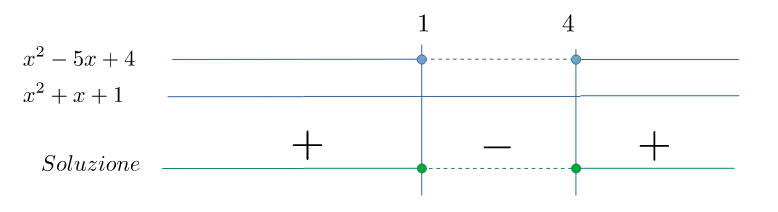
Soluzione finale
Il segno della frazione è dato dal segno del numeratore (il denominatore è sempre positivo). Viene richiesto di cercare i valore negativi o uguali a zero, pertanto la soluzione finale è $$\mathcal{S}=\left\{1\leqslant x\leqslant 4\right\}$$
In termini di intervalli: $$[1, 4]$$
Esempio 5
Risolvere $${{x^2-5x+4\over 9-4x^2}\geqslant 0}$$
Soluzione
Moltiplichiamo per $-1$ la disequazione per rendere il denominatore più facile da studiare, i.e. $${x^2-5x+4\over 4x^2-9}\leqslant 0$$
Studio del segno del numeratore
Zeri: $$x^2-5x+4=0\;\implies\;x_{1,2}={5\pm\sqrt{25-16}\over 2}={5\pm3\over 2}=\left\{4,\ 1\right\}$$
Segno del numeratore ($a=1$ quindi è positivo o uguale a zero per valore esterni): $$x^2-5x+4\geqslant0\;\implies\;\left\{x\leqslant1\right\} \;\lor\; \left\{x\geqslant4\right\}$$
Studio del segno del denominatore
Zeri: $$4x^2-9=0\;\implies\;x_{1,2}=\pm{3\over2}$$
Segno del denominatore ($a>0$ quindi è positivo e diverso da zero per valore esterni): $$4x^2-9>0\;\implies\;\left\{x<-{3\over2}\right\} \;\lor\; \left\{x>{3\over2}\right\}$$
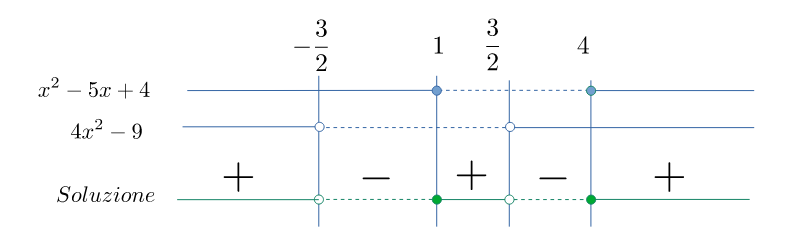
Soluzione finale
Il segno della frazione è dato dal segno del numeratore combinato con quello del denominatore. Viene richiesto di cercare i valore negativi (abbiamo trasformato la disequazione) o uguali a zero, pertanto la soluzione finale è $$\mathcal{S}=\left\{-{3\over2} < x \leqslant1\right\}\;\lor\;\left\{{3\over2} < x \leqslant4\right\}$$
In termini di intervalli: $$\left(-{3\over2},1\right]\cup \left({3\over2},4 \right]$$
Esempio 6
Risolvere $${{x\cdot (x^2-4)\over (x^2-3)(x^2-8x+12)}\leqslant 0}$$
Soluzione
Studiamo i singoli fattori ricordando che il denominatore non può assumere valori pari a zero.
Fattore 1:
$$x>0$$
Fattore 2
$$x^2-4 \geqslant 0\;\implies\;x^2\geqslant4 \;\implies\; \left\{x\leqslant-2\right\} \;\lor\;\left\{x\geqslant2\right\}$$
Fattore 3
$$x^2-3 > 0\;\implies\;x^2>3 \;\implies\; \left\{x<\sqrt{3}\right\} \;\lor\;\left\{x>\sqrt{3}\right\}$$
Fattore 4
$$x^2-8x+12=0\;\implies\;x_{1,2}={8\pm\sqrt{64-48}\over 2}={8\pm4\over 2}=\left\{6,\ 2\right\}$$
$$x^2-8x+12>0\;\implies\; \left\{x<2\right\} \;\lor\;\left\{x>6\right\}$$
Soluzione finale (parte negativa)
Attenzione che il punto $2$ pur essendo uno zero del fattore 2, è da escludere perché non fa parte delle condizioni di esistenza (zero del fattore 4)
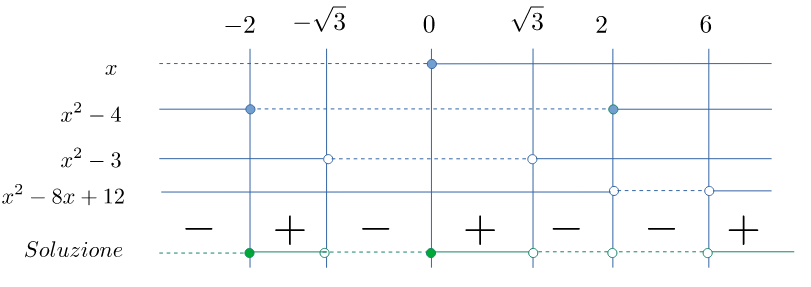
La soluzione è: $$ \mathcal{S}= \left\{x\leqslant-2\right\}\;\lor\;\left\{-\sqrt{3}<x\leqslant 0\right\}\;\lor\;\left\{\sqrt{3}<x<2\right\}\;\lor\;\left\{2<x<6\right\} $$
In termini di intervalli: $$ \left(-\infty,\ -2\right] \cup \left(-\sqrt{3},\ 0\right] \cup \left(\sqrt{3},\ 2\right) \cup \left(2,\ 6\right) $$
Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).
