Disequazioni biquadratiche e reciproche

Obiettivo (corso Analisi Matematica 1)

• Biquadratiche
• Trasformazione per riduzione al secondo grado

Indice degli esempi

Risolvere

1. $x^4-2x^2-8\leqslant 0$
2. $x^4-2x^2\geqslant0$
3. $x^{10}-x^6\leqslant0$
4. $2x^4+x^3-6x^2+x+2 \leqslant 0$

Biquadratiche

Sono disequazioni di grado maggiore al secondo ma che con l'ausilio di un'opportuna trasformazione possono essere ricondotte a disequazioni di secondo grado, i.e. sono del tipo

$${ax^{2n}+bx^n+c\lesseqgtr0}$$

La disequazione va risolta nei seguenti passi:

1. Si esegue la sostituzione $t=x^n$ arrivando alla disequazione $$at^2+bt+c\lesseqgtr0$$
2. Si risolve la disequazione quadratica trovando la validità di $t$
3. Si risolve la disequazione in $x$ sapendo la validità di $t$

Esempio 1

Risolvere $${x^4-2x^2-8\leqslant 0}$$

Soluzione

Con la sostituzione $t=x^2$ la disequazione diventa $$t^2-2t-8\leqslant 0$$

Gli zeri dell'equazione sono $$t_{1,2}={2\pm\sqrt{4+32}\over 2}={2\pm6\over 2}=\left\{4,\ -2\right\}$$

Quindi, essendo $a>0$ e i valori cercati minori o uguali a zero, la soluzione della disequazione in $t$ è (valori interni) $$ -2\leqslant t\leqslant 4 $$ o riscritta come sistema $$\begin{cases} t\geqslant -2\\ t\leqslant 4 \end{cases}$$

Con la trasformazione utilizzata, $t=x^2$ le disequazioni precedenti diventano: $$\begin{cases} x^2\geqslant -2\\ x^2\leqslant 4 \end{cases}$$

La prima disequazione $x^2\geqslant -2$ è sempre verificata, i.e. ha soluzione $$\mathbb{R}$$ mentre la seconda ha soluzione $$\left\{-2\leqslant x\leqslant 2\right\}$$

Intersecano le due soluzione si ottiene la soluzione finale $$\mathcal{S} = \left\{-2\leqslant x\leqslant 2\right\}$$

Esempio 2

Risolvere $${x^4-2x^2\geqslant0}$$ in due modi diversi (annullamento del prodotto e biquadratica).

Soluzione

Due strategie possibili:

• Soluzione con annullamento del prodotto
• Soluzione con biquadratica

Soluzione con annullamento del prodotto

La disequazione può essere riscritta come $$x^2(x^2-2)\geqslant0$$

Il segno di $x^2$ è sempre positivo e uguale a zero per $x=0$.

Il segno di $x^2-2\geqslant0$ è $$-\sqrt{2}\leqslant x \leqslant \sqrt{2}$$

Il segno è riportato in figura.

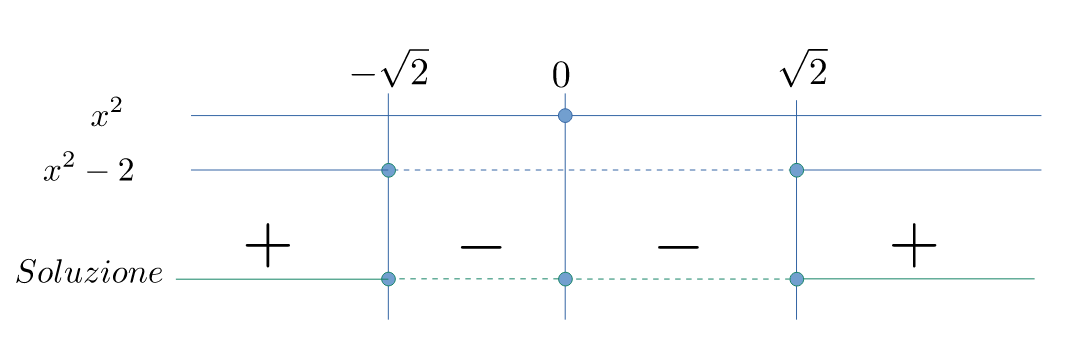
La soluzione finale è $$\mathcal{S}=\left\{x\leqslant -\sqrt{2}\right\}\;\lor\;\left\{0\right\}\;\lor\;\left\{x\geqslant \sqrt{2}\right\}$$

Soluzione con biquadratica

Con la sostituzione $t=x^2$ la disequazione diventa $$t^2-2t\geqslant0$$ che ha soluzione $$\left\{t\leqslant0\right\}\;\lor\;\left\{t\geqslant2\right\}$$

Quindi dobbiamo unire le seguenti due disequazioni nella variabile $x$:

$$ x^2\leqslant 0 \quad\lor\quad x^2\geqslant 2 $$

La prima $x^2\leqslant 0$ ha soluzione $\left\{x=0\right\}$

La seconda $x^2\geqslant 2$ ha soluzione $$\left\{x\leqslant -\sqrt{2}\right\}\;\lor\;\left\{x\geqslant \sqrt{2}\right\}$$

La soluzione finale $\mathcal{S}$ si ottiene unendo le due soluzioni

$$\mathcal{S}=\left\{x\leqslant -\sqrt{2}\right\}\;\lor\;\left\{0\right\}\;\lor\;\left\{x\geqslant \sqrt{2}\right\}$$

Esempio 3

Risolvere $${x^{10}-x^6\leqslant0}$$

Soluzione

La disequazione può essere riscritta come $$x^6(x^4-1)\leqslant0$$

Applichiamo la regola dei segni.

Il fattore $x^6$ è sempre positivo e vale $0$ in $x=0$.

Quindi ci basta studiare $$x^4-1\leqslant 0$$ che con il cambio di variabile $t=x^2$ diventa $t^2-1\leqslant 0$

Quindi $t^2-1\leqslant 0$ ha soluzione $$-1\leqslant t\leqslant 1$$

Con il cambio originario se deve risolvere il sistema di disequazioni $$\begin{cases} t\geqslant -1\\ t\leqslant 1\\ \end{cases} \;\implies\; \begin{cases} x^2\geqslant -1\\ x^2\leqslant 1\\ \end{cases} $$

La cui soluzione finale è $$-1\leqslant x\leqslant 1$$

Essendo $x^6$ sempre positivo e vale zero quando $x=0$ la soluzione finale è

$$ \mathcal{S} = \left\{-1\leqslant x\leqslant 1\right\} $$

Reciproche

Sono qui introdotte più per curiosità che utilità per esercizi che capitano agli esami.

Un polinomio $P(x)$ è detto a radici reciproche se $x_0$ è una radice allora anche ${1\over x_0}$ è una radice.

Se si esegue la trasformazione ${t=x+{1\over x}}$ allora si semplifica l'espressione polinomiale.

Ad esempio, un polinomio quarto grado a radici reciproche è della forma $$ {ax^4+bx^3+cx^2+bx+a \lesseqgtr 0} $$

Dividendo per $x^2$ (sempre positivo) e l'espressione polinomiale diventa $$ a\left(x^2+{1\over x^2}\right) +b \left(x+{1\over x}\right) + c \lesseqgtr 0 \;\implies\; a\left(x+{1\over x}\right)^2-2a+b \left(x+{1\over x}\right) + c \lesseqgtr 0 $$

introducendo il cambio di variabile $t=x+{1\over x}$ si ha $$ at^2 + bt + c-2a \lesseqgtr 0 $$

Esempio 4

Risolvere $${2x^4+x^3-6x^2+x+2 \leqslant 0}$$

Soluzione

La disequazione può essere riscritta (dividendo prima per $x^2$) come $$ 2\left(x^2+{1\over x^2}\right) +\left(x+{1\over x}\right) -6 \leqslant 0 \;\implies\; 2\left(x+{1\over x}\right)^2-4+\left(x+{1\over x}\right) -6\leqslant 0 $$

Con la sostituzione $t=x+{1\over x}$ si ha $$ 2t^2+t-10\leqslant 0 $$

Ha radici $$ t_{1,2} = {-1\pm\sqrt{1+80}\over 4} = {-1\pm9\over 4} = \left\{2,\ -{5\over 2}\right\} $$ e quindi soluzione $$ -{5\over 2}\leqslant t\leqslant 2 $$

Quindi, ritornando alla sostituzione originaria, dobbiamo risolvere $$\begin{cases} t\geqslant -{5\over 2}\\ t\leqslant 2\\ \end{cases} \;\implies\; \begin{cases} x+{1\over x}\geqslant -{5\over 2}\\ x+{1\over x}\leqslant 2\\ \end{cases}$$

La disequazione $$x+{1\over x}\geqslant -{5\over 2}\;\implies\;{2x^2+5x+2\over 2x}\geqslant 0$$ ha soluzione $$\left\{-2\leqslant x \leqslant -{1\over 2}\right\}\;\lor\; \left\{x>0\right\}$$

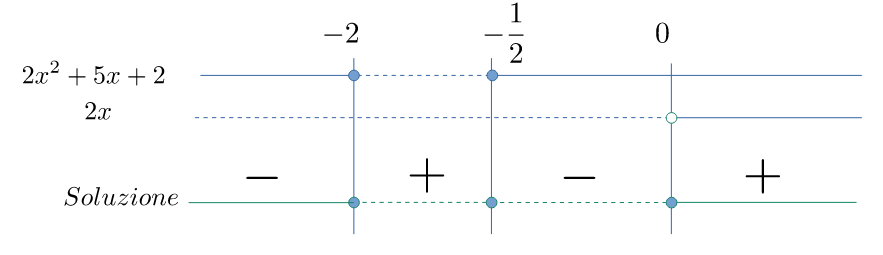
La disequazione $$x+{1\over x}\leqslant 2\;\implies\;{x^2-2x+1\over x}\leqslant 0\;\implies\;{(x-1)^2\over x}\leqslant 0$$ ha soluzione $$\left\{x <0\right\}\;\lor\; \left\{1\right\}$$

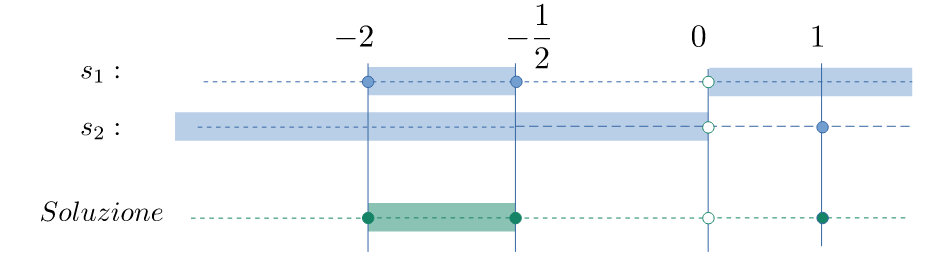
Intersecando le due soluzioni

$$\left\{-2\leqslant x \leqslant -{1\over 2}\right\}\;\lor\; \left\{x>0\right\}$$

e

$$\left\{x <0\right\}\;\lor\; \left\{1\right\}$$

si ha la soluzione finale

$$ \mathcal{S} = \left\{-2\leqslant x \leqslant -{1\over 2}\right\}\;\lor\; \left\{1\right\} $$

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).