Disequazioni di grado superiore al secondo

Obiettivo (corso Analisi Matematica 1)

• Teorema fondamentale dell'algebra (conseguenza)
• Fattorizzazione
• Studio dei segni
• Esempi

Indice degli esempi

Risolvere

1. $3 x^3 - 2 x^2 - 6 x + 4 \geqslant 0$
2. $x^5 - x^3 + 2 x^2 - 6 x + 4 < 0$

Teorema fondamentale dell'algebra (conseguenza)

Ogni polinomio di grado $n\geqslant 1$ a coefficienti reali si può scomporre nel prodotto di fattori reali di I o II grado (riducibili o meno)

• Se i fattori di II grado sono irriducibili: il segno è sempre positivo o negativo

Disequazione modello

$${\operatorname{Fattore}_1 \cdot \operatorname{Fattore}_2 \cdot \ldots \cdot \operatorname{Fattore}_n \lesseqgtr 0}$$

dove un singolo fattore è:

• equazione di I grado
• equazione di II grado

Procedura generale

1. Fattorizzazione del polinomio
2. Studio del segno dei singoli fattori ("+" e "-")
3. Studio del segno generale, come prodotto dei segni dei singoli fattori

Esempi

Esempio 1

Risolvere $${3 x^3 - 2 x^2 - 6 x + 4 \geqslant 0}$$

Soluzione: fattorizzazione

Si trova che $x=2/3$ è radice, infatti $$ \begin{array}{c|c c c|c} &3& -2& -6& +4\\ 2/3& & +2& 0& -4\\ \hline &3& 0& -6& 0\\ \end{array} $$

Da cui la fattorizzazione $3 x^3 - 2 x^2 - 6 x + 4 = \left(x-2/3\right)(3x^2-6)$

Gli zeri di $3x^2-6$ sono $x^2=2 \implies x=\left\{\pm\sqrt{2}\right\}$

Soluzione: segno del fattore 1

$\left(x-2/3\right) \geqslant 0 \implies x \geqslant {2\over 3}$

Soluzione: segno del fattore 2

Gli zeri di $3x^2-6$ sono $x^2=2 \implies x=\left\{\pm\sqrt{2}\right\}$

$3x^2-6 \geqslant 0 \implies \left\{x\leqslant -\sqrt{2}\right\} \lor\left\{x\geqslant \sqrt{2}\right\}$

Soluzione: segno finale

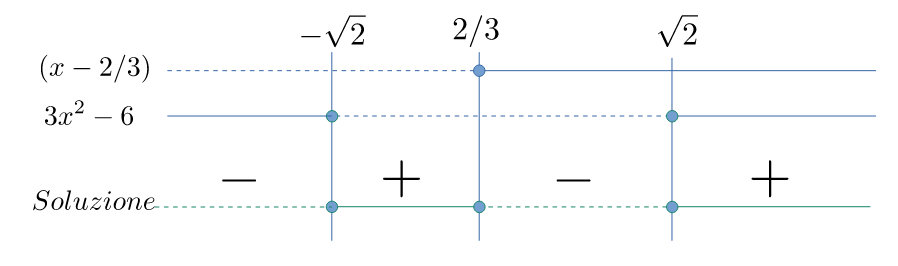
Soluzione: $\left\{-\sqrt{2}\leqslant x \leqslant{2\over3}\right\} \lor\left\{x\geqslant\sqrt{2}\right\}$

Esempio 2

Risolvere $${P(x) = x^5 - x^3 + 2 x^2 - 6 x + 4 < 0}$$

Soluzione: fattorizzazione

Le radici razionali di $P(x)$ sono da ricercare nell'insieme $\left\{\pm1, \pm2, \pm4\right\}$

• Per $x=-1$ si ha $P(-1) = -1+1+2+6+4 \ne 0 \implies$ non è una radice
• Per $x=1$ si ha $P(1) = 1-1+2-6+4 = 0 \implies$ è una radice

$$ \begin{array}{c|c c c c c|c} &1& 0& -1& 2& -6& +4\\ 1 & & 1& 1& 0& 2& -4\\ \hline &1& 1& 0& 2& -4& 0\\ \end{array} $$ da cui la fattorizzazione $P(x) = (x-1)(x^4+x^3+2x-4)$

Le radici razionali di $P_1(x)=x^4+x^3+2x-4$ sono da ricercare nell'insieme $\left\{\pm1, \pm2, \pm4\right\}$

• Per $x=-1$ si ha $P_1(-1) = 1-1+2-4 \ne 0 \implies$ non è una radice
• Per $x=1$ si ha $P_1(1) = 1+1+2-4 = 0 \implies$ è una radice $$ \begin{array}{c|c c c c|c} &1& 1& 0& 2& -4\\ 1 & & 1& 2& 2& 4\\ \hline &1& 2& 2& 4& 0\\ \end{array} $$ da cui la fattorizzazione

Le radici razionali di $P_2(x)=x^3+2x^2+2x+4$ sono da ricercare nell'insieme $\left\{\pm1, \pm2, \pm4\right\}$

• Per $x=-1$ si ha $P_2(-1) = 1+2+2+4 \ne 0 \implies$ non è una radice
• Per $x=1$ si ha $P_2(1) = -1+2-2+4 \ne 0 \implies$ non è una radice
• Per $x=-2$ si ha $P_2(1) = -8+8-4+4 = 0 \implies$ è una radice

$$ \begin{array}{c|c c c|c} &1& 2& 2& 4\\ -2 & & -2& 0& -4\\ \hline &1& 0& 2& 0\\ \end{array} $$ da cui la fattorizzazione $$P(x) = (x-1)^2(x^3+x^2+2x+4) = (x-1)^2(x+2)(x^2+2)$$

Soluzione: studio dei segni (da escludere l'uguaglianza)

• $(x-1)^2$ è sempre positivo (per $x=1$ è zero)
• $(x+2) > 0$ per $x\geqslant -2$ (è zero per $x=-2$)
• $x^2+2$ è irriducibile e in questo caso sempre positivo

Soluzione: combinazione dei segni

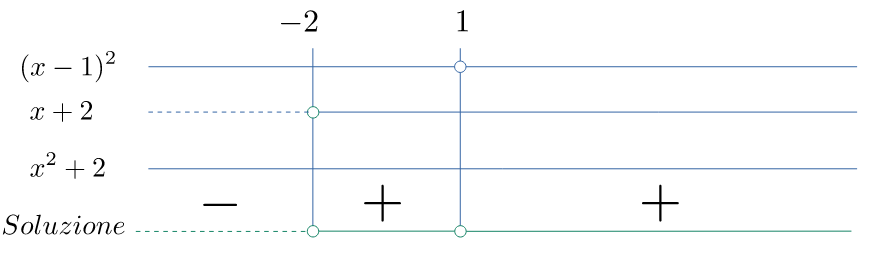
Soluzione: $\left\{x<-2\right\}$

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).