Equazioni e disequazioni di secondo grado
Obiettivo (corso Analisi Matematica 1)
- Equazione di secondo grado
- due radici reali distinte
- due radici reali coincidenti
- nessuna radice reale
- Interpretazione geometrica: parabola
- Disequazione di secondo grado
Indice degli esempi
Risolvere
- $2x^2+x-1 = 0$
- $-x^2-2x-1 = 0$
- $x^2+1 = 0$
Fattorizzare
- $-4x^2+4x-1 = 0$
- $x^2 + 1=0$
- $-4x^2+4x-2=0$
Studiare le seguenti disequazioni
- $x^2-5x+6 \lesseqgtr 0$
- $x^2-4x+4 \lesseqgtr 0$
- $x^2-4x+5 \lesseqgtr 0$
- $-x^2+5x-6 \lesseqgtr 0$
- $-x^2+4x-4 \lesseqgtr 0$
- $-x^2+4x-6 \lesseqgtr 0$
Equazione di secondo grado (definizione)
L'equazione $${ax^2+bx+c = 0,\quad a\ne0}$$ ha soluzione $${x_{1,2} = {-b \pm \sqrt{b^2 - 4ac} \over 2a}}$$
Equazione di secondo grado
Dimostrazione
Moltiplico per $4a$ l'equazione:
$$4 a^{2} x^{2} + 4abx + 4ac=0$$
Aggiungo e tolgo $b^2$:
$$4 a^{2} x^{2} + 4abx + b^2 = b^2 - 4ac$$
Quadrato di un binomio:
$$(2ax + b)^2 = b^2 - 4ac$$
Eseguo radice e isolo $x$:
$$x_{1,2} = {-b \pm \sqrt{b^2 - 4ac} \over 2a}$$
Discussione delle radici
Posto $${\Delta = b^2 - 4ac}$$ si ha $${x_{1,2} = {-b \pm \sqrt{\Delta} \over 2a}}$$
- Se $\Delta > 0$: due soluzione reali distinte
- Se $\Delta = 0$: due soluzione reali coincidenti
- Se $\Delta < 0$: nessuna soluzione
Esempi
Esempio 1: due radici reali distinte
Calcolare $${2x^2+x-1 = 0}$$
Soluzione
$$2x^2+x-1 = 0 \implies\Delta = 1^2 - 4\cdot 2\cdot(-1) = 9 > 0$$
Radici: $x_{1,2} = {-1 \pm 3 \over 2\cdot 2} = \left\{{1\over 2},\ -1\right\}$
Esempio 2: Due radici reali coincidenti
Calcolare $${-x^2-2x-1 = 0}$$
Soluzione
$$-x^2-2x-1 = 0 \implies\Delta = (-2)^2 - 4\cdot (-1)\cdot(-1) = 4 - 4 = 0$$
Radici: $x_{1,2} = {2 \pm 0 \over 2\cdot (-1)} = -1$
Esempio 3: Nessuna radice reale
Calcolare $${x^2+1 = 0}$$
Soluzione
$$x^2+1 = 0 \implies\Delta = 0^2 - 4\cdot 1\cdot1 = -4 < 0$$
Infatti, somma di due quadrati sempre positivi
Casi notevoli
Monomia: $b=0$ e $c=0$
$${ax^2=0} \implies x_{1,2}=0$$
Spuria: $c=0$
$${ax^2+bx=0} \implies x(ax+b)=0 \implies x_{1}=0 \quad {\text{e}}\quad x_{2}=-{\frac {b}{a}}$$
Una radice è sempre lo zero
Casi notevoli
Pura: $b=0$
$${ax^2+c=0} \implies x^2 = -{c\over a}$$
- Se $-{c\over a} < 0 \implies$ nessuna soluzione
- Se $-{c\over a} > 0 \implies x_{1,2}=\pm {\sqrt {-{\frac {c}{a}}}}$
Le radici sono simmetriche rispetto allo zero
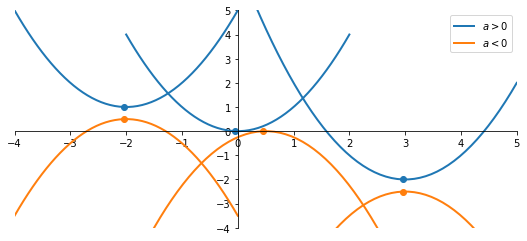
Interpretazione geometrica: parabola
Sia $${y = ax^2 + bx + c}$$ allora
Concavità
- se $a>0$ verso l'alto
- se $a<0$ verso il basso
Vertice
- $x_v = -{b\over2a}$
- $y_v = -{\Delta\over 4a}$
Relazioni tra radici e coefficienti
Somma
$$ \begin{aligned} {s}={x_{1}+x_{2}} &= {\frac {-b-{\sqrt {b^{2}-4ac}}}{2a}}+{\frac {-b+{\sqrt {b^{2}-4ac}}}{2a}} \\ &= {\frac {-2b}{2a}}={-{\frac {b}{a}}} \end{aligned} $$
Prodotto
$$ \begin{aligned} {p}={x_{1}x_{2}} &= {\frac {(-b-{\sqrt {b^{2}-4ac}})(-b+{\sqrt {b^{2}-4ac}})}{4a^{2}}} \\ &= {\frac {(-b)^{2}-({\sqrt {b^{2}-4ac}})^{2}}{4a^{2}}} = {\frac {b^{2}-b^{2}+4ac}{4a^{2}}} = {{\frac {c}{a}}} \end{aligned} $$
Fattorizzazione
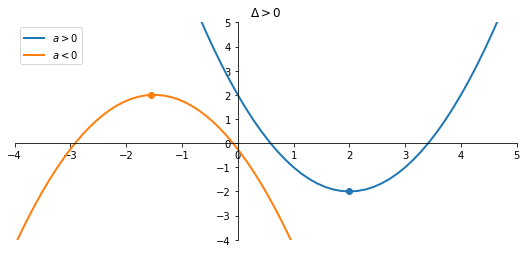
Caso $\Delta > 0$
Date le radici $x_{1,2}$ si ha $${ax^2+bx+c = a(x-x_1)(x-x_2)}$$
Prodotto di due termini lineari
Esempio
Fattorizzare $${2x^2+x-1 = 0}$$
Soluzione
$$x_{1,2} = {-1 \pm \sqrt{1^2 + 4\cdot 2\cdot1} \over 2\cdot 2} = {-1 \pm \sqrt{9} \over 4} = {-1 \pm 3 \over 4} = \left\{{1\over 2},\ -1\right\}$$
Fattorizzazione: $2\left(x-{1\over 2}\right)(x+1) = (2x-1)(x+1)$
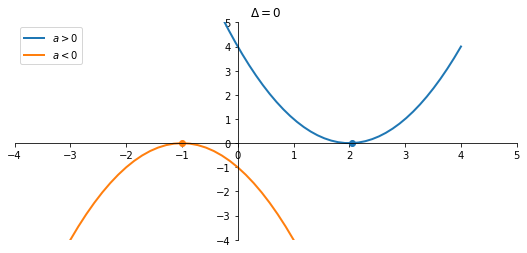
Caso $\Delta = 0$
Date radici coincidenti $x_{1,2}=x_0$ si ha $${ax^2+bx+c = a(x-x_0)(x-x_0) = a(x-x_0)^2}$$
Termine quadratico
Esempio 4
Fattorizzare $${-4x^2+4x-1 = 0}$$
Soluzione
$$x_{1,2} = {-4 \pm \sqrt{4^2 - 4\cdot (-4)\cdot(-1)} \over 2\cdot (-4)} = {-4 \pm \sqrt{0} \over -8} = {1\over 2} = \left\{{1\over 2}\right\}$$
Fattorizzazione: $-4\left(x-{1\over 2}\right)^2 = -\left(2\left(x-{1\over 2}\right)\right)^2 = -(2x-1)^2$
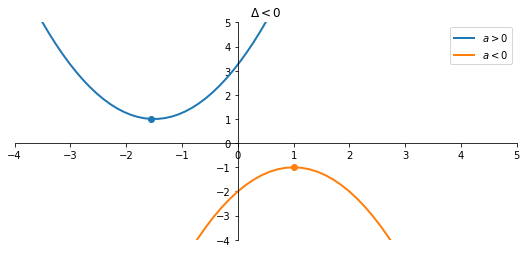
Caso $\Delta < 0$
Dal completamento del quadrato nella dimostrazione della formula risolutiva, possiamo scrivere
$$ ax^2 + bx + c \;=\;{1\over 4a}(2ax + b)^2 - {\Delta\over 4a} \;=\; a \left[ \left(x - \left(-{b\over 2a}\right) \right)^2 - {\Delta \over 4a^2} \right] $$
Somma di due quadrati sempre positivi o sempre negativi
Il termine $-{b\over 2a}$ è $x_v$, il vertice della parabola
Esempio 5 e 6
Esempio 5: Somma positiva
${x^2 + 1=0} \implies\Delta = -4 <0$
Esempio 6: Somma negativa
$-4x^2+4x-2=0 \implies\Delta = 16 - 4(-4)(-2) = -16 <0$
Da $x_{v} = -{b\over 2a} = -{4\over 2(-4)} = {1\over2}$ si ha la fattorizzazione $$ -4 \left[ \left(x-{1\over2}\right)^2 - {-16\over4 \cdot 16} \right] = - \left[ (2x-1)^2 + 1 \right] $$
Senza ricordare la formula basta completare il quadrato, e si ha $$ {-4x^2+4x-2} \;=\; -(4x^2-4x+2) \;=\; -\big( (2x-1)^2 -1 +2\big) \;=\; {-\big( (2x-1)^2 +1 \big)} $$
Disequazione di secondo grado
$${ax^2+bx+c \lesseqgtr 0,\quad a\ne0}$$
- Approccio per via grafica (veloce)
- Analitico
Approccio per via grafica
1: Disegnare la parabola
- segno di $\Delta$ e relative radici $x_{1,2}$ (3 casi)
- $\Delta>0$, $\Delta=0$, $\Delta<0$
- segno di $a$ (2 casi)
- $a>0$, $a<0$
- Totale casi possibili: 6
2: Individuare la regione di interesse della soluzione:
- $\geqslant$, $>$, $=$, $\ne$, $<$, $\leqslant$
Analizziamo i diversi casi possibili
Esempio 7: caso $a > 0$ e $\Delta > 0$
Studiare $${x^2-5x+6 \lesseqgtr 0}$$
Soluzione
Delta: $\Delta = (-5)^2 - 4 \cdot 1 \cdot 6 = 25-24=1 > 0$
Radici: $x_{1,2} = {5 \pm 1\over 2} = \left\{2,\ 3\right\}$
Segno di $a$: $a>0$
Eseguo il disegno della parabola e individuo il segno della funzione nelle diverse parti del dominio
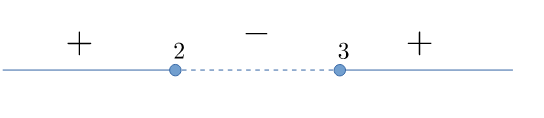
Esempio 7: caso $a > 0$ e $\Delta > 0$

- $x^2-5x+6 \geqslant 0 \implies \left\{x\leqslant2 \right\} \lor \left\{x\geqslant3\right\}$ (valori esterni compresi gli zeri)
- $x^2-5x+6 > 0 \implies \left\{x<2\right\} \lor \left\{x>3\right\}$ (valori esterni esclusi gli zeri)
- $x^2-5x+6 = 0 \implies x\in \left\{2,\ 3\right\}$ (gli zeri)
- $x^2-5x+6 \ne 0 \implies x\not\in \left\{2,\ 3\right\}$ (zeri esclusi)
- $x^2-5x+6 < 0 \implies \left\{2 < x< 3\right\}$ (valori interni esclusi gli zeri)
- $x^2-5x+6 \leqslant 0 \implies \left\{2 \leqslant x \leqslant 3\right\}$ (valori interni compresi gli zeri)
Esempio 8: caso $a > 0$ e $\Delta = 0$
Studiare $${x^2-4x+4 \lesseqgtr 0}$$
Soluzione
Delta: $\Delta = (-4)^2 - 4 \cdot 1 \cdot 4 = 16 - 16 = 0$
Radici: $x_{1,2} = {4 \pm 0\over 2} = \left\{2\right\}$
Segno di $a$: $a>0$
Eseguo il disegno della parabola e individuo il segno della funzione nelle diverse parti del dominio
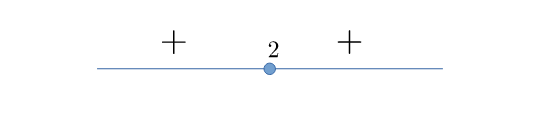
- $x^2-4x+4 \geqslant 0 \implies x\in\mathbb{R}$ (tutti)
- $x^2-4x+4 > 0 \implies x\in\mathbb{R}\setminus \left\{2\right\}$ (tutti tranne lo zero)
- $x^2-4x+4 = 0 \implies x\in \left\{2\right\}$ (lo zero)
- $x^2-4x+4 \ne 0 \implies x\in\mathbb{R} \setminus \left\{2\right\}$ (lo zero escluso)
- $x^2-4x+4 < 0 \implies \left\{\emptyset\right\}$ (nessuno)
- $x^2-4x+4 \leqslant 0 \implies x\in \left\{2\right\}$ (solo lo zero)
Esempio 9: caso $a > 0$ e $\Delta < 0$
Studiare $${x^2-4x+5 \lesseqgtr 0}$$
Soluzione
Delta: $\Delta = (-4)^2 - 4 \cdot 1 \cdot 5 = 16 - 20 = -4 < 0$
Nessuna radice reale
Segno di $a$: $a>0$
Eseguo il disegno della parabola e individuo il segno della funzione nelle diverse parti del dominio
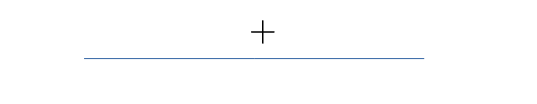
- $x^2-4x+4 \geqslant 0 \implies x\in\mathbb{R}$ (tutti)
- $x^2-4x+4 > 0 \implies x\in\mathbb{R}$ (tutti)
- $x^2-4x+4 = 0 \implies \left\{\emptyset\right\}$ (nessuno)
- $x^2-4x+4 \ne 0 \implies x\in\mathbb{R}$ (tutti)
- $x^2-4x+4 < 0 \implies \left\{\emptyset\right\}$ (nessuno)
- $x^2-4x+4 \leqslant 0 \implies \left\{\emptyset\right\}$ (nessuno)
Caso $a < 0$
Due soluzioni possibili:
- analoghi ragionamenti come sopra (disegno della parabola diverso)
- moltiplicare per $-1$ e cambiare verso alla disuguaglianza
Qui faremo vedere la scelta 1 perché lo studente deve essere veloce nel risolvere le disequazioni di secondo grado
Esempio 10: caso $a < 0$ e $\Delta > 0$
Studiare $${-x^2+5x-6 \lesseqgtr 0}$$
Soluzione
Delta: $\Delta = 5^2 - 4 \cdot (-1) \cdot (-6) = 1 > 0$
Radici: $x_{1,2} = {-5 \pm 1\over -2} = \left\{2,\ 3\right\}$
Segno di $a$: $a<0$
Eseguo il disegno della parabola e individuo il segno della funzione nelle diverse parti del dominio
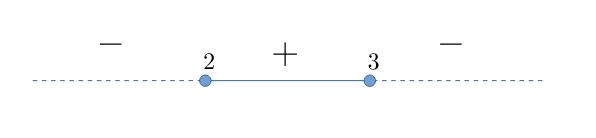
- $-x^2+5x-6 \geqslant 0 \implies \left\{2 \leqslant x \leqslant 3\right\}$
- $-x^2+5x-6 > 0 \implies \left\{2 < x < 3\right\}$
- $-x^2+5x-6 = 0 \implies x\in \left\{2,\ 3\right\}$
- $-x^2+5x-6 \ne 0 \implies x\not\in \left\{2,\ 3\right\}$
- $-x^2+5x-6 < 0 \implies \left\{x < 2\right\} \lor\left\{x > 3\right\}$
- $-x^2+5x-6 \leqslant 0 \implies \left\{x \leqslant 2\right\} \lor\left\{x \geqslant 3\right\}$
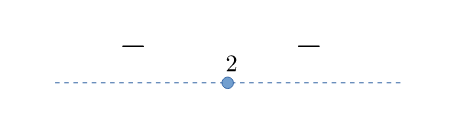
Esempio 11: caso $a < 0$ e $\Delta = 0$
Studiare $${-x^2+4x-4 \lesseqgtr 0}$$
Soluzione
Delta: $\Delta = 4^2 - 4 \cdot (-1) \cdot (-4) = 0$
Radici: $x_{1,2} = {-4 \pm 0\over -2} = \left\{2\right\}$
Segno di $a$: $a<0$
Eseguo il disegno della parabola e individuo il segno della funzione nelle diverse parti del dominio
- $-x^2+4x-4 \geqslant 0 \implies x\in \left\{2\right\}$
- $-x^2+4x-4 > 0 \implies \left\{\emptyset\right\}$
- $-x^2+4x-4 = 0 \implies x\in \left\{2\right\}$
- $-x^2+4x-4 \ne 0 \implies x\in\mathbb{R}\setminus \left\{2\right\}$
- $-x^2+4x-4 < 0 \implies x\in\mathbb{R}\setminus \left\{2\right\}$
- $-x^2+4x-4 \leqslant 0 \implies x\in\mathbb{R}$
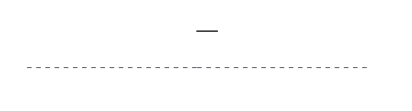
Esempio 12: caso $a < 0$ e $\Delta < 0$
Studiare $${-x^2+4x-6 \lesseqgtr 0}$$
Soluzione
Delta: $\Delta = 4^2 - 4 \cdot (-1) \cdot (-6) = 16 - 24 = -8 < 0$
Nessuna radice reale
Segno di $a$: $a<0$
Eseguo il disegno della parabola e individuo il segno della funzione nelle diverse parti del dominio
- $-x^2+4x-6 \geqslant 0 \implies \left\{\emptyset\right\}$
- $-x^2+4x-6 > 0 \implies \left\{\emptyset\right\}$
- $-x^2+4x-6 = 0 \implies \left\{\emptyset\right\}$
- $-x^2+4x-6 \ne 0 \implies x\in\mathbb{R}$
- $-x^2+4x-6 < 0 \implies x\in\mathbb{R}$
- $-x^2+4x-6 \leqslant 0 \implies x\in\mathbb{R}$
Approccio per via analitica
L'approccio per via analitica si base sulla fattorizzazione del polinomio e sulla legge dell'annullamento del prodotto
Lo vediamo applicato ai casi di polinomi di grado maggiore del due
Per quelli di grado 2 è più semplice e soprattutto veloce analizzare i casi per via grafica
Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).
