Equazioni e disequazioni di primo grado

Obiettivo (corso Analisi Matematica 1)

• Equazione di primo grado e sua interpretazione geometrica
• Disequazioni di primo grado
• Esempi

Indice degli esempi

Risolvere le seguenti equazioni

1. ${3x-5\over2}-{3-x\over 3}={x+1\over 3}-{10\over 3}$
2. $(t+1)x-2t=0$ al variare di $t$ e successivamente, trovare quel valore di $t$ per cui lo zero è uguale a $1$ e a $2$
3. $-2x-3=0$
4. $-2x-3<0$
5. $-2x-3>0$
6. $1-{x-9\over 6}-{x\over2}\leqslant{3x+1\over15}-{x\over2}-{13\over15}$

Equazione di primo grado (definizione)

Un'equazione di I grado è un'equazione della forma $${ax+b = 0,\quad a\ne0}$$ la cui soluzione è $${ax+b=0 \quad\implies\quad x = - {b\over a}}$$

Equazione di primo grado

Dimostrazione

Per risolvere l'equazione isolo il termine $x$, i.e.

$$\begin{gathered} ax+b = 0\\ ax = -b \\ x = -{b\over a} \end{gathered}$$

dove l'ultima divisione è possibile se $a\ne 0$

Nota: Se $a=0$ in $ax+b = 0$ allora

• se $b=0$ ci sono infinite soluzioni (caso indeterminato, i.e. $0\cdot x = 0\implies 0=0$)
• se $b\ne0$ non c'è soluzione (caso impossibile, i.e. $0\cdot x = b\ne0\implies 0\ne0$)

Interpretazione geometrica: retta

L'equazione $${y = ax +b}$$ rappresenta una retta

Si ha

• se $a>0$ è un retta crescente
• se $a<0$ è una retta decrescente
• se $b=0$ allora $y=ax$ è una retta che passa per l'origine $(0,0)$

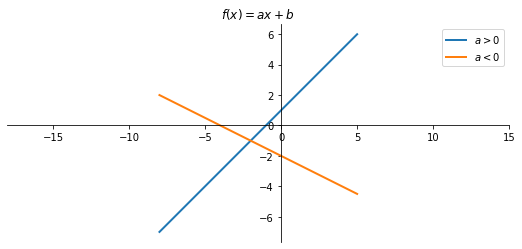
Equazione parametrica della retta

Un'equazione $ax+b=0$ dove $a$ e/o $b$ dipendono da un parametro ad esempio $t$, i.e. sono della forma

$${ \begin{cases} a = a(t)\\ b = b(t) \end{cases} }$$

si dice che l'equazione è parametrica nel parametro $t$

Esempi di equazioni

Esempio 1

Risolvere la seguente equazione $${{3x-5\over2}-{3-x\over 3}={x+1\over 3}-{10\over 3}}$$

Soluzione

Semplifichiamo il lato sinistro dell'equazione

$$ {3x-5\over2}-{3-x\over 3}={x-9\over 3} $$

Eseguiamo il denominatore comune (m.c.m.) ai due membri dell'equazione e lo eliminiamo (moltiplicando i due membri dell'equazione per la stessa quantità)

$$ {3(3x-5)-2(3-x)\over \cancel{6}}={2(x-9)\over \cancel{6}} $$

Semplifichiamo poi l'espressione e la risolviamo

$$ 9x+2x-2x=-18+15+6 \quad\implies\quad 9x=3 \quad\implies\quad x = {3\over9}={1\over 3} $$

Esempio 2

Risolvere al variare di $t$, l'equazione $${(t+1)x-2t=0\,.}$$ Successivamente, trovare quel valore di $t$ per cui lo zero è uguale a $1$ e a $2$.

Soluzione

Si tratta di un'equazione parametrica in $t$.

La soluzione dell'equazione $(t+1)x-2t=0$, è

$$ x = {2t\over t+1} $$

se $t+1\ne 0$, i.e. $t\ne-1$

Quindi si devono discutere i seguenti due casi: $t\ne-1$ e $t=-1$

Caso $t=-1$

Se $t = -1$, l'equazione diventa $2=0$ e quindi non ci sono soluzioni (caso impossibile)

Caso $t\ne-1$

Se $t\ne-1$, la soluzione è $x = {2t\over t+1}$

Per trovare il valore di $t$ per cui lo zero $x = {2t\over t+1}$ sia uguale a $1$ o a $2$ dobbiamo risolvere le seguenti equazioni

• ${2t\over t+1} = 1 \;\implies\; 2t = t+1\;\implies\; t = 1$
• ${2t\over t+1} = 2 \;\implies\; 2t = 2(t+1)\;\implies\; 0 = 2$ (impossibile)

Disequazioni di primo grado

Disequazioni di primo grado

Disequazioni di I grado: $${ax+b > 0}$$

• caso $a>0$
• caso $a<0$

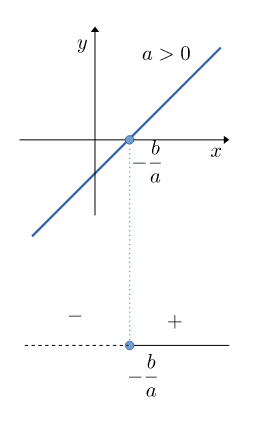
Caso $a>0$

$$ \begin{gathered} ax + b > 0,\quad a>0 \\ \Downarrow\\ x > - {b\over a} \end{gathered} $$

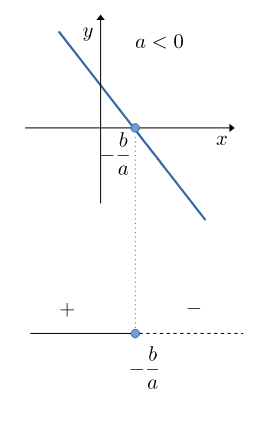
Caso $a<0$

$$ \begin{gathered} ax + b > 0,\quad a<0 \\ \Downarrow\\ x < - {b\over a} \end{gathered} $$

Esempi di disequazioni

Esempio 3

Risolvere: $${-2x-3=0}$$

Soluzione

$$-2x-3=0 \;\implies\; -2x = 3 \;\implies\; x = -{3\over 2}$$

Esempio 4

Risolvere: $${-2x-3<0}$$

Soluzione

$$-2x-3 < 0 \;\implies\; -2x < 3 \;\implies\; x > -{3\over 2}$$

Esempio 5

Risolvere: $${-2x-3\geqslant0}$$

Soluzione 3

$$-2x-3\geqslant0 \;\implies\; -2x \geqslant 3 \;\implies\; x \leqslant -{3\over 2}$$

Esempio 6

Risolvere la seguente disequazione $${1-{x-9\over 6}-{x\over2}\leqslant{3x+1\over15}-{x\over2}-{13\over15}}$$

Soluzione

Semplifichiamo la disequazione eliminando il termine uguale che compare a sinistra e a destra. i.e. ${x\over2}$

$$ {6-(x-9)\over 6}\leqslant{3x+1-13\over15} $$

$$ {-x+15\over 6}\leqslant{3x-12\over15} $$

Eseguiamo il denominatore comune (m.c.m.)

$$ {-x+15\over 3\cdot 2}\leqslant{3x-12\over5\cdot 3} $$

Eliminiamo il denominatore comune (moltiplicando i due membri dell'equazione per la stessa quantità)

$$ {5(-x+15)\over \cancel{5\cdot3\cdot 2}}\leqslant{2(3x-12)\over\cancel{5\cdot3\cdot 2}} $$

Semplifichiamo l'espressione e la risolviamo facendo attenzione ad un eventuale segno meno cambia il verso della disequazione

$$ -5x+75\leqslant 6x-24 $$

Semplifichiamo l'espressione

$$ -11x\leqslant -99 \quad\implies\quad x\geqslant {-99\over -11} \quad\implies\quad x\geqslant 9 $$

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).