Principio induzione

Obiettivo (corso Analisi Matematica 1)

Definizione di successione
Il principio di induzione
- Prima forma
- Seconda forma
Esempio notevoli con il principio di induzione
- Progressione aritmetica
- Progressione geometrica

Successioni

Definizione
Se per ogni numero naturale $n\in\mathbb{N}={0,1,2,\cdots}$ associamo un elemento dell'insieme $A$ nell'ordine $${a_0,\ a_1,\ a_2,\ \cdots ,\ a_n,\ \cdots}$$ creiamo una successione e la indicheremo brevemente con la scrittura ${{a_n}}$

Nota:

La successione ha il primo termine $a_0$, il secondo termine $a_1$ e così via
$a_{i+1}$ è il successore di $a_i$, mentre $a_i$ è il precedente di $a_{i+1}$

Esempio: successione costante

$${{a_n} = {a}\quad \forall n\in\mathbb{N}}$$

$a_0 = a$
$a_1 = a$
$a_2 = a$
$\ldots$

Esempio

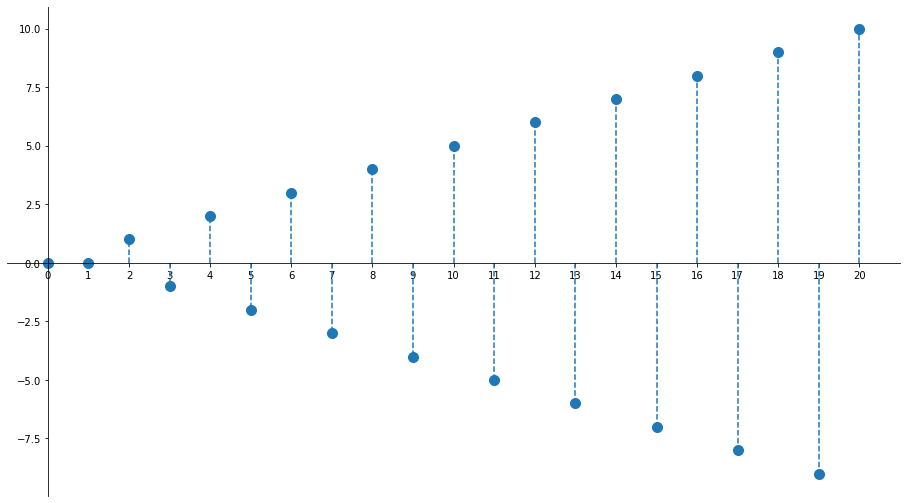
Scrivere i primi elementi della successione (fino a $a_5$):

$${a_n}=\begin{cases}{n\over2}&\text{se }n\text{ è pari}\\-{n-1\over2}&\text{se }n\text{ è dispari} \end{cases}$$

. . .

Soluzione

per $n=0 \implies a_0=0$
per $n=1 \implies a_1=0$
per $n=2 \implies a_2=1$
per $n=3 \implies a_3=-1$
per $n=4 \implies a_4=2$
per $n=5 \implies a_5=-2$

Si ha

$$ \big\{0,\ 0,\ 1,\ -1,\ 2,\ -2,\ \cdots\big\} $$

Il principio di induzione

Il principio di induzione si usa per dimostrare la validità delle proposizioni/teoremi che sono della forma: $${\text{Dimostrare che per ogni numero naturale vale qualcosa}}$$
La cosa principale da osservare è che quel "qualcosa" è formulato sui numeri naturali

Buon ordinamento di $\mathbb{N}$

$0\in\mathcal{S}$
$\forall n\in\mathcal{S} \implies n+1\in\mathcal{S}$

allora

$\mathcal{S} = \mathbb{N}$

cioè ogni numero naturale ha il suo successore (buon ordinamento)

Teorema (principio di induzione) [prima forma]

Sia $P(n)$ un'affermazione che dipende da $n\in\mathbb{N}$.
Se

Passo base: $\mathcal{P}(0)$ è vera

Passo induttivo: $\forall n\in\mathbb{N},\quad \mathcal{P}(n) \implies \mathcal{P}(n+1)$
allora segue la verità di $\mathcal{P}(n)$ per ogni $n$.

Per capire il principio di induzione graficamente immaginiamo delle tessere del domino disposte in fila e ci chiediamo se cadranno tutte.

Il principio di induzione afferma che

Passo base: posso far cadere la prima tessera del domino;
Passo induttivo: se le tessere del domino sono disposte in modo tale che, se una qualsiasi di loro cade, cadendo colpisce e fa cadere anche la successiva tessera ho provato che le mie tessere del domino cadranno tutte.

Operativamente:

Il passo base è tipicamente facile perché richiede la verifica della proprietà per il primo punto della sequenza, i.e. $\mathcal{P}(0)$ è vera (di solito $0$ o $1$)
Il passo induttivo è più complicato e richiede di dimostrare la verità di $\mathcal{P}(n+1)$ a partire dalla verità di $\mathcal{P}(n)$: tipicamente si parte da $\mathcal{P}(n+1)$ e attraverso delle manipolazioni algebriche la si riscrive in funzione di $\mathcal{P}(n)$ e quindi si sfrutta la validità di $\mathcal{P}(n)$ per provare la validità di $\mathcal{P}(n+1)$.

Tutti questi passaggi saranno più chiari con gli esempi che seguiranno.

Esempio

Dimostrare che $$2^{n}>n\quad\forall n\in\mathbb{N}$$

Soluzione (Passo base)

Per $n=0$ si ha $2^0= 1 > 0$.

Soluzione (Passo induttivo)

Osserviamo che $2^{n}\geqslant 1$ per ogni $n\in\mathbb{N}$, quindi $$2^{n+1} = 2^{n}\cdot 2 = 2^{n} + 2^{n} > n + 1$$ che è l'affermazione $n+1$-esima.

Teorema (principio di induzione) [seconda forma]

Sia $P(n)$ un'affermazione che dipende da $n\in\mathbb{N}$.
Se

Passo iniziale: $\mathcal{P}(0)$ è vera

Passo induttivo: $\forall n\in\mathbb{N},\quad \left(\mathcal{P}(0) \land \mathcal{P}(1) \land \ldots \land \mathcal{P}(n)\right) \implies \mathcal{P}(n+1)$ cioè dalla verità di tutte le affermazioni precedenti a $\mathcal{P}(n)$ segue la verità di $\mathcal{P}(n+1)$

Nota:

Assume vere tutte le preposizioni da $0$ a $n$ per provare la verità di $n+1$
è poco utilizzato negli esercizi

Esempi

Esempio: progressione aritmetica

Dimostrare che $$S(n)=\sum\limits_{i=1}^{n} i = {n(n+1)\over 2}\quad\forall n\in\mathbb{N}\land n\geqslant1$$

Dimostrazione (per induzione)

Passo base

$$S(1)=\sum\limits_{i=1}^{1} i = 1 = {1 \cdot (1+1)\over 2} = 1$$

Passo induttivo

$$\begin{aligned} S(n+1) = \sum\limits_{i=1}^{n+1} i &= \sum\limits_{i=1}^{n} i + (n+1) \\ &= \underbrace{{n(n+1)\over 2}}_{S(n)} + (n+1) \\ &= (n+1)\left({n\over 2}+1\right) \;=\; \underbrace{{(n+1)(n+2)\over 2}}_{S(n+1)} \end{aligned}$$

Esempio: progressione geometrica

Dimostrare che $${\sum\limits_{i=0}^{n} r^{i} = \frac{1-r^{n+1}}{1-r}\quad\forall n\in\mathbb{N} \land r\ne1}$$

Dimostrazione (per induzione)

Passo base(con $r\ne1$)

$$\sum\limits_{i=0}^{0} r^{i} = r^{0} = 1 = \frac{1-r^{1}}{1-r} = 1$$

Passo induttivo (con $r\ne1$)

$$\begin{aligned} \sum\limits_{i=0}^{n+1} r^{i} &= \sum\limits_{i=0}^{n} r^{i} + r^{n+1} = \frac{1-r^{n+1}}{1-r} + r^{n+1} \\ &= \frac{1-r^{n+1} + (1-r)r^{n+1}}{1-r} = \frac{1-\cancel{r^{n+1}} + \cancel{r^{n+1}} -r^{n+2}}{1-r}\\ &= \frac{1 - r^{n+2}}{1-r} \end{aligned}$$

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).