Esercizi (base) sul valore assoluto
Indice esericizi (corso Analisi Matematica 1)
Risolvere le seguenti disequazioni con il valore assoluto
- $|x|>x$
- $|2-x| < 1$
- $|x+2|<|1-x|$
- $|x-3| < |x+1|$
- $|x+5| > |1-x|$
- $\big|1-|x|\big|<1$
Studiare
- $\bigg| \Big| \big| |x| + x \big| + x \Big| + x \bigg|$
Esercizi
Esercizio 1
Risolvere la seguente disequazione: $${|x|>x}$$
Soluzione
Dalla definizione di valore assoluto si ha $$ |x|={\begin{cases}x,&{\text{se }}x\geqslant 0\\-x,&{\text{se }}x<0\end{cases}} $$
Caso: $x\geqslant 0$
Per $x\geqslant 0$ la disequazione diventa $$x>x$$ e quindi non c'è soluzione
Caso: $x< 0$
Per $x < 0$ la disequazione diventa $$-x>x\;\implies\;-2x>0\;\implies\;x<0$$ e quindi tutte le $x<0$ sono soluzione
Soluzione finale
Unendo le due soluzioni, l'insieme soluzione $\mathcal{S}$ è: $$\mathcal{S}={x<0}$$
Esercizio 2
Risolvere $${|2-x| < 1}$$
Soluzione
Osserviamo che $|2-x| = |x-2|$ (preferisco avere la $x$ con segno positivo)
Posto $t=x-2$, la disequazione diventa $|t|<1$ che ha soluzione $\left\{-1 < t < 1\right\}$
Quindi, si ha: $$-1 < t < 1 \implies-1 < x-2 < 1 \implies 1 < x < 3$$
Se non fosse stata eseguita la trasformazione $|2-x| = |x-2|$, la disequazione da risolvere sarebbe stata $$-1 < 2-x < 1$$ ovvero $$-3 < -x < -1$$ i.e.
- $-3 < -x \implies x < 3$
- $-x < -1 \implies x > 1$
che corrisponde a $$1 < x < 3$$
Esercizio 3
Risolvere la seguente disequazione: $${|x+2|<|1-x|}$$
Soluzione
Bisogna distinguere diversi casi per eliminare il valore assoluto mettendo il segno corretto positivo o negativo all'espressione al suo interno
Quindi,
- $x+2\geqslant 0$ per $x\geqslant -2$
- $1-x\geqslant 0$ per $-x\geqslant -1\;\implies\;x \leqslant1$
Casi possibili:
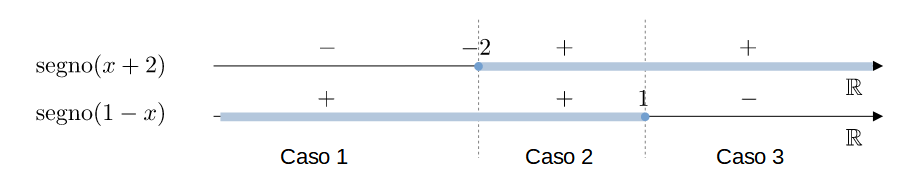
Bisogna analizzare i seguenti casi:
- $x\leqslant -2$
- $x+2$ ha segno negativo
- $1-x$ ha segno positivo
- $-2 < x\leqslant 1$
- $x+2$ ha segno positivo
- $1-x$ ha segno positivo
- $x> 1$
- $x+2$ ha segno positivo
- $1-x$ ha segno negativo
Caso 1
Per $x\leqslant -2$ la disequazione diventa $$-(x+2)<1-x\;\implies\;-2<1$$ che ha soluzione per ogni $x$ (nel dominio di riferimento, i.e. $x\leqslant -2$)
Caso 2
Per $-2 < x\leqslant 1$ la disequazione diventa $$(x+2)<1-x\;\implies\;2x<-1\;\implies x\leqslant -{1\over 2}$$ che quindi ha soluzione per ogni $-2 <x\leqslant -{1\over 2}$
Caso 3
Per $x> 1$ la disequazione diventa $$(x+2)<-(1-x)\;\implies\;2<-1\;\implies x=\emptyset$$
La soluzione finale si ottiene unendo le singole soluzioni, che diventa:
$$ \mathcal{S} = \left\{x\leqslant -2 \;\lor\;-2 <x\leqslant -{1\over 2}\right\} = \left\{x\leqslant -{1\over 2}\right\} $$
Esercizio 4
Risolvere $${|x-3| < |x+1|}$$
Soluzione
Dobbiamo distinguere i diversi casi
$|x-3| = \left\{\begin{matrix} -(x-3),& x-3<0 \\ x-3,& x-3 \geqslant 0 \end{matrix}\right. \implies |x-3| = \left\{\begin{matrix} -x+3,& x<3 \ x-3,& x \geqslant 3 \end{matrix}\right.$
$|x+1| = \left\{\begin{matrix} -(x+1),& x+1<0 \\ x+1,& x+1 \geqslant 0 \end{matrix}\right. \implies |x+1| = \left\{\begin{matrix} -x-1,& x<-1 \\ x+1,& x \geqslant -1 \end{matrix}\right.$
Casi possibili:
- $x < -1$
- $-1 \leqslant x \leqslant 3$
- $x>3$

Caso 1: $x < -1$
$-x+3 < -x-1 \implies 3 < -1 \implies \left\{\emptyset\right\}$
Caso 2: $-1 \leqslant x \leqslant 3$
$-x+3 < x+1 \implies x > 1 \implies \left\{1 < x \leqslant 3\right\}$
Caso 3: $x>3$
$x-3 < x+1 \implies -3 < 1 \implies \left\{x>3\right\}$
Soluzione (unione): $x>1$
Esercizio 5
Risolvere $${|x+5| > |1-x|}$$
Soluzione
Dobbiamo distinguere i diversi casi
$|x+5| = \left\{\begin{matrix} -x-5,& x<-5 \\ x+5,& x \geqslant -5 \end{matrix}\right.$
$|1-x| = \left\{\begin{matrix} -1+x,& x\geqslant 1 \\ 1-x,& x \leqslant 1 \end{matrix}\right.$
Casi possibili:
- $x < -5$
- $-5 \leqslant x \leqslant -1$
- $x>-1$

Caso 1: $x < -5$
$-x-5 > 1-x \implies -5 > 1 \implies \left\{\emptyset\right\}$
Caso 2: $-5 \leqslant x \leqslant -1$
$x+5 > 1-x \implies x > -2 \implies \left\{-2 < x \leqslant -1\right\}$
Caso 3: $x>-1$
$x+5 > -1+x \implies 5 > -1 \implies \left\{x>-1\right\}$
Soluzione(unione): $x>-2$

Esercizio 6
Risolvere la seguente disequazione: $${\big|1-|x|\big|<1}$$
Soluzione
Eliminiamo il valore assoluto più interno riscrivendo la disequazione come segue (applichiamo la definizione di valore assoluto a $|x|$): $$ {\begin{cases}|1-x|<1,&{\text{se }}x\geqslant 0\|1+x|<1,&{\text{se }}x<0\end{cases}} $$
Studiamo la prima disequazione
Studiamo il segno di ${1-x}$, per ${x\geqslant 0}$
Si ha $$1-x\geqslant0\;\implies x\leqslant 1$$
Quindi, si ha
- per $0\leqslant x\leqslant 1$ la disequazione diventa $$1-x<1\;\implies x>0$$ quindi ha soluzione $0<x\leqslant 1$
- per $x> 1$ (e quindi anche $x\geqslant 0$) la disequazione diventa $$-(1-x)<1\;\implies x<2$$ quindi ha soluzione $1<x< 2$
Quindi per $x\geqslant0$ la soluzione è (unendo le due soluzioni precedenti): $$0<x<2$$
Studiamo la seconda disequazione
Si potrebbero fari tutti i conti precedenti con il nuovo caso (fate voi!)
E' più facile notare che se sostituisco la $x$ con $-x$ la disequazione non cambia
$$\big|1-|x|\big|<1$$
Infatti vedremo in seguito che c'è una simmetria pari
Questo porta a dire che la soluzione del secondo caso è $$-2<x<0$$
Soluzione finale
La soluzione finale si ottiene unendo le due soluzioni parziali, ottenendo l'insieme $$\mathcal{S}=\left\{-2<x<0\;\lor\;0<x<2\right\}$$

Esercizio 7
Studiare $${\bigg| \Big| \big| |x| + x \big| + x \Big| + x \bigg|}$$
Soluzione
$|x|= \left\{\begin{matrix} -x,& x<0 \\ x,& x\geqslant0 \end{matrix}\right.$
$|x| + x = \left\{\begin{matrix} -x+x=0,& x<0 \\ x+x=2x,& x\geqslant0 \end{matrix}\right.$
$\big||x| + x\big| = \left\{\begin{matrix} 0,& x<0 \\ 2x,& x\geqslant0 \end{matrix}\right.$
$\big||x| + x\big| + x = \left\{\begin{matrix} x,& x<0 \\ 3x,& x\geqslant0 \end{matrix}\right.$
$\Big|\big||x| + x\big| + x\Big| = \left\{\begin{matrix} -x,& x<0 \\ 3x,& x\geqslant0 \end{matrix}\right.$
$\Big|\big||x|+ x\big| + x\Big| + x = \left\{\begin{matrix} 0,& x<0 \\ 4x,& x\geqslant0 \end{matrix}\right.$
$\bigg|\Big|\big||x| + x\big| + x\Big| + x\bigg| = \left\{\begin{matrix} 0,& x<0 \\ 4x,& x\geqslant0 \end{matrix}\right.$
Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).
