Sostieni il corso con una donazione PayPal

(PayPal.Me/ManoloVenturin)

Il valore assoluto

Obiettivo (corso Analisi Matematica 1)

  • Definizione di valore assoluto (o modulo)
  • Proprietà del valore assoluto
  • disuguaglianze di base con il valore assoluto e loro interpretazione grafica
    • $|x| \leqslant a$
    • $|x| \geqslant a$
  • VIDEO
  • PDF

    • Valore assoluto (o modulo)

    Definizione
    Il valore assoluto (o modulo) di un numero reale $x$, è definito come $${|x|={\begin{cases}x,&{\text{se }}x\geqslant 0\\-x,&{\text{se }}x<0\end{cases}}}$$

    Grafico:


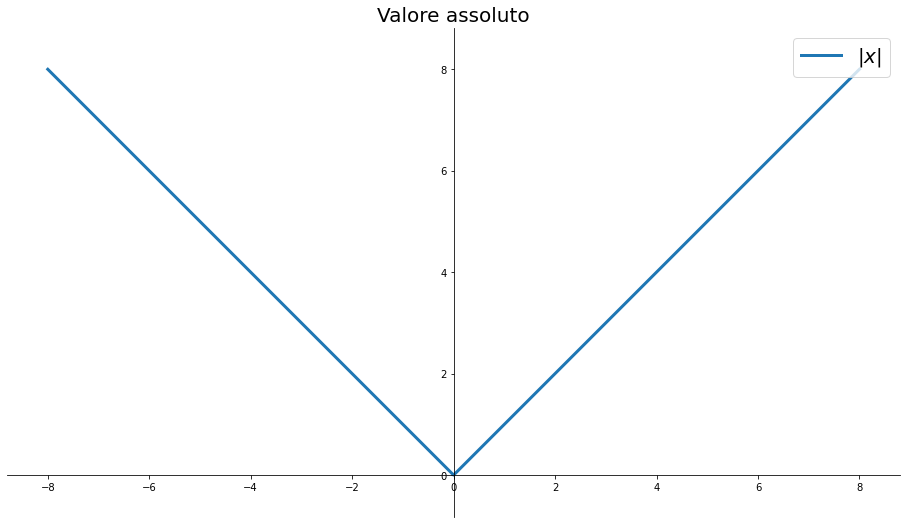
    Distanza

    La quantità $${|x-y|}$$ con $x,\,y\in\mathbb{R}$ prende il nome di distanza tra $x$ e $y$.

    Nota: Il valore assoluto è la distanza di $x$ da $0$


    Proprietà

    Siano $a$, $x$, $y$ numeri reali e $a>0$, allora

    • $|x|\geqslant0$ e $|x|=0 \;\iff\;x=0$
    • $|x|=|-x|$
    • $|x\cdot y| = |x|\cdot|y|$
    • $|x|\leqslant a \;\iff\; -a\leqslant x\leqslant a$
    • $|x|\geqslant a \;\iff\; x\leqslant-a\;\lor\;x\geqslant a$

    Nota: Se $a<0$ allora

    • $|x|\leqslant a \;\iff\; x\in\emptyset$
    • $|x|\geqslant a \;\iff\; x\in\mathbb{R}$

    • Disuguaglianza triangolare: $$|x+y|\leqslant |x|+|y|$$
    • Nella dis. triangolare il segno di uguale vale solo se $x\geqslant 0$ e $y\geqslant 0$
    • Disuguaglianza triangolare inversa: $$\big||x|-|y|\big|\leqslant |x-y|$$

    Nota: $\sqrt{x^2}=|x|$ (alcuni autori definiscono il valore assoluto in questo modo)


    Interpretazione grafica delle diseguaglianze di base

    Si ha che $|x|<a$, corrisponde a $$-a<x<a$$


    Si ha che $|x|>a$, corrisponde a $$x<-a\;\lor\;x>a$$


    Interpretazione della disuguaglianza $|x|>a$ attraverso il grafico della funzione

    Valori esterni per avere un valore assoluto maggiore di $a$



    Disequazioni di base (in dettaglio)



    Studiamo $|x| \leqslant a$

    • se $a < 0 \implies \left\{\emptyset\right\}$
    • se $a = 0 \implies \left\{0\right\}$
    • se $a > 0 \implies \left\{-a < x < a\right\} = (a,\ a)$
    • se $a \geqslant 0 \implies \left\{-a \leqslant x \leqslant a\right\} = [a,\ a]$


    Studiamo $|x| \geqslant a$

    • se $a < 0 \implies \mathbb{R}$
    • se $a = 0 \implies \mathbb{R}$
    • se $a > 0 \implies \left\{x < -a\right\} \;\lor\; \left\{x > a\right\} = (-\infty,\ a) \;\lor\; (a,\ +\infty)$
    • se $a \geqslant 0 \implies \left\{x \leqslant a\right\} \;\lor\; \left\{x \geqslant a\right\} = \left(-\infty,\ a\right] \;\lor\; \left[a,\ +\infty\right)$


    Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).