I numeri reali (dagli assiomi) e i reali estesi

Obiettivo (corso Analisi Matematica 1)

Definizione di numero reale per via assiomatica
Ordinamento nei reali
Assioma di Dedekind
Regole di calcolo nei reali
- Legge di annullamento del prodotto
Densità dei reali
Definizione di numero reale esteso

VIDEO

PDF

Assiomi dei numeri reali

Definizione per via assiomatica (regole primitive non dimostrabili)

Esistono diverse formalizzazioni tra loro equivalenti, qui ne riportiamo una

In $\mathbb{R}$ sono definite:

due operazioni
- una detta somma "$+$" e
- l'altra detta moltiplicazione "$\cdot$"
e una relazione d'ordine "$<$" che verificano le seguenti proprietà (assiomi)

Assiomi dei numeri reali

Siano $a$, $b$ e $c$ tre numeri appartenenti a $\mathbb{R}$, allora

Proprietà associativa dell'addizione e della moltiplicazione:$$\begin{aligned} (a+b)+c&=a+(b+c)\\ (a\cdot b)\cdot c&=a\cdot(b\cdot c) \end{aligned}$$
Proprietà commutativa dell'addizione e della moltiplicazione$$\begin{aligned} a+b&=b+a\\ a\cdot b&=b\cdot a \end{aligned}$$

Esistenza degli elementi neutri, $0$ per l'addizione e $1$ per la moltiplicazione, tali che:$$\begin{aligned} a+0&=a\\ a\cdot 1&=a \end{aligned}$$
Esistenza dell'opposto rispetto l'elemento neutro dell'addizione: $$a+(-a)=0$$
Esistenza dell'inverso rispetto l'elemento neutro della moltiplicazione, se $a\ne0$ si ha: $$a\cdot a^{-1}=1$$ dove $a^{-1}$ si indica anche con $1\over a$
Proprietà distributiva della moltiplicazione verso l'addizione: $$a\cdot(b+c)=a\cdot b + a\cdot c$$

Legge di tricotomia: ovvero dati due numeri $a$ e $b$ vale solo una delle seguenti possibilità: $$a < b \quad,\quad a > b \quad,\quad a=b$$
Transitiva dell'ordinamento: $$\left.\begin{aligned} a < b\\ b < c \end{aligned}\right\} \implies a<c $$
Compatibilità dell'ordinamento rispetto alla somma: $$a< b \implies a+c< b+c$$
Compatibilità dell'ordinamento rispetto al prodotto: $$\left.\begin{aligned} a < b\\ c>0 \end{aligned}\right\} \implies a\cdot c<b\cdot c $$
Vale l'assioma di separazione (o assioma di Dedekind o completezza): Siano $A,B \in\mathbb{R}$ non vuoti e tali che per ogni $a \in A$ e $b \in B$ si abbia $a \leqslant b$. Allora esiste un elemento $c \in\mathbb{R}$ che separa $A$ e $B$, cioè tale che per ogni $a \in A$ e $b \in B$ si ha $a\leqslant c \leqslant b$ .

Ordinamento

Per l'ordinamento abbiamo: $$a\leqslant b \iff a < b \;\lor\; a=b$$ i.e. $$a < b \iff a \leqslant b \;\land\; a\ne b$$

Inoltre, si ha $$a\geqslant b\iff b\leqslant a$$

Assioma di Dedekind

Gli assiomi precedenti non sono sufficienti a caratterizzare completamente $\mathbb{R}$

Assioma di separazione
Se $A$ e $B\ne\emptyset$ tali che $a\leqslant b$ per ogni $a\in A$ e per ogni $b\in B$, allora esiste $x\in\mathbb{R}$ tale che $$a\leqslant x \leqslant b$$

Teorema di buona definizione di $\mathbb{R}$
Esiste ed è unico un insieme $\mathbb{R}$ che verifica gli assiomi precedentemente elencati. Inoltre $\mathbb{Q}\subset\mathbb{R}$ e le operazione di $\mathbb{Q}$ (somma, prodotto, ordinamento totale) su $\mathbb{R}$ sono coerenti con quelle di $\mathbb{Q}$.

Regole di calcolo

Discendono dagli assiomi le classiche regole di calcolo usate per semplificare le espressioni:

Moltiplicazione per zero: $$a\cdot0=0$$
Regole dei segni: $$(-a)\cdot b= - a\cdot b\quad\text{ e }\quad(-a)\cdot (-b)= a\cdot b$$
L'opposto dell'opposto è il numero di partenza: $$-(-a) = a$$
Semplificazione rispetto alla somma: $$a+b=a+c \implies b=c$$
Semplificazione rispetto al prodotto: $$a\cdot b=a\cdot c \implies b=c,\quad \text{se }a\ne0$$
L'opposto è unico
L'inverso (di un numero diverso da $0$) è unico
Cambio di segno della diseguaglianza: $$a>0\implies -a<0$$
Regola di cambio di segno nelle disequazioni: $$\begin{aligned}a\leqslant b\;\text{ e }\;c\geqslant0\implies a\cdot c\leqslant b\cdot c\ a\leqslant b\;\text{ e }\;c\leqslant0\implies a\cdot c\geqslant b\cdot c\end{aligned}$$
Il quadrato di un numero è positivo: $$a^2>0$$ e $a^2=0\iff a=0$
Legge annullamento del prodotto: se $a\cdot b=0$ sse $a=0$ o $b=0$

Il punto 11 spiega perché non possiamo dividere per $0$, cioè non esiste l'inverso dello zero. Per l'assioma dell'esistenza degli inversi si avrebbe $0\cdot 0^{-1}=1$ che è in contraddizione con la legge dell'annullamento del prodotto $0\cdot 0^{-1} = 0$.

I numeri reali: conseguenze

$\mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q}\subset \mathbb{R}$
Le operazioni di somma, prodotto e ordinamento totale su $\mathbb{R}$ sono coerenti con quelle di $\mathbb{Q}$
E' possibile rappresentare $\mathbb{R}$ geometricamente con una retta orientata

Assioma di Dedekind (interpretazione grafica)

Permette di avere una corrispondenza biunivoca tra tutti i punti della retta e i numeri reali (continuo di punti)

E' importante notare che $\mathbb{Q}$ non verifica l'assioma di Dedekind.

L'insieme $A={x\in \mathbb {R} \colon\; x^{2}<2}$ ha come estremo superiore $\sqrt{2}\not\in\mathbb{Q}$.

Altre proprietà

Proprietà di Archimede
Per ogni $x,\,y\in\mathbb{R}$ con $x,y>0$ esiste $n\in\mathbb{N}$ tale che $n x>y$

Parte intera
Per ogni $x\in\mathbb{R}$ esiste un unico $n\in\mathbb{Z}$ tale che $$n\leqslant x < n+1$$
$n$ viene indicato con $\lfloor x \rfloor$ (si legge parte bassa)

Densità

$\mathbb{N}$ è superiormente illimitato
$\mathbb{Z}$ è superiormente e inferiormente illimitato
$\mathbb{N}\subset \mathbb{Z}\subset \mathbb{Q}\subset \mathbb{R}$
Gli insiemi dei razionali $\mathbb{Q}$
- non è completo (es. $\sqrt{2}\not\in\mathbb{Q}$)
- è numerabile (corrispondenza biunivoca con i numeri naturali, come da figura)

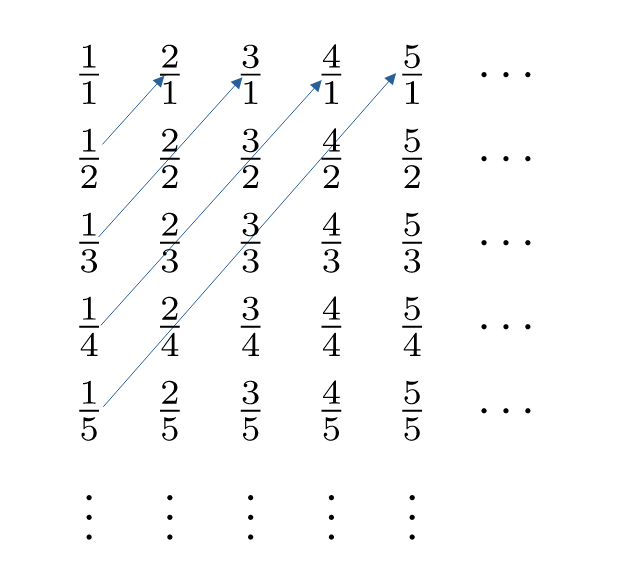
Gli insiemi dei razionali è
- denso nei reali
  - ${x\in\mathbb{R}\colon\; a<x<b,\ a<b} \cap \mathbb{Q}\ne \emptyset$
- posso approssimare un numero reale tramite un numero razionale con precisione grande a piacere
  - per ogni $a\in\mathbb{R}$ si ha $\sup{x\in\mathbb{Q}\colon\; x<a} = a$ (approx. per eccesso)
  - per ogni $a\in\mathbb{R}$ si ha $\inf{x\in\mathbb{Q}\colon\; x>a} = a$ (approx. per difetto)

Reali estesi (definizione)

Conviene, per semplificare le notazioni future, introdurre i numeri reali estesi, ovvero introdurre un simbolo per un numero arbitrariamente (infinitamente) grande e il suo opposto, i.e. $$ \overline{\mathbb{R}} = \mathbb{R}\cup {-\infty} \cup {+\infty} $$ dove i simboli $-\infty$ e $+\infty$ indicano due oggetti che supporremo tali che $$\begin{gathered} \forall x\in\mathbb{R}\colon\; -\infty < x\\ \forall x\in\mathbb{R}\colon\; x < +\infty \end{gathered}$$

Capire l'assioma di Dedekind

Il numero $0.999\ldots$ e $1$ rappresentano lo stesso numero reale

L'assioma di Dedekind sostanzialmente dice che: "tra due numeri reali diversi riesco sempre a scrivere un numero reale che stia in mezzo e li separi"

Provate a trovare un numero che separi $0.\overline{9}$ e $1$

Una spiegazione alternativa di questo fatto lo vedremo quando parleremo delle successioni

Curiosità

Il tappare i buchi dei razionali con i reali è dovuto a Cauchy (con le sue successioni) e poi da Cantor e Dedekind
La necessità dei reali rispetto ai razionali è necessaria al calcolo infinitesimale che fu inventato Newton e Leibniz
Ora il calcolo infinitesimale si chiama analisi matematica
Il tappare i buchi si traduce nel dire che i numeri reali sono uno "spazio metrico completo"

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).