Funzioni elementari - parte 2

Obiettivo (corso Analisi Matematica 1)

Potenza con esponente intero pari e dispari
Radice di esponente intero pari e dispari
Potenza con esponente razionale

VIDEO

PDF

Potenza con esponente intero pari

$${f(x)=x^{2n},\quad n\in\mathbb{N},\quad n\geqslant 1}$$

Proprietà:

Pari
Dominio: $\mathbb{R}$
Codominio: $\left[0,+\infty\right)$
Strettamente crescente su $\left[0,+\infty\right)$
(e ivi invertibile)
Strettamente decrescente su $\left(-\infty,0\right]$
Per $0\leqslant x \leqslant 1$ si ha $x^{2(n+1)} \leqslant x^{2n}$
Per $x \geqslant 1$ si ha $x^{2(n+1)} \geqslant x^{2n}$

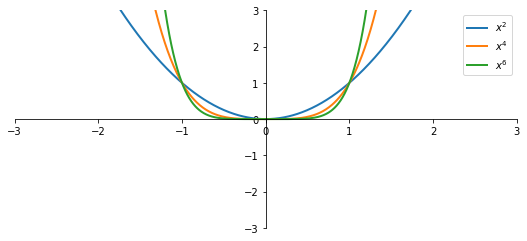
Potenza con esponente intero pari

$${f(x)=x^{2n},\quad n\in\mathbb{N},\quad n\geqslant 1}$$

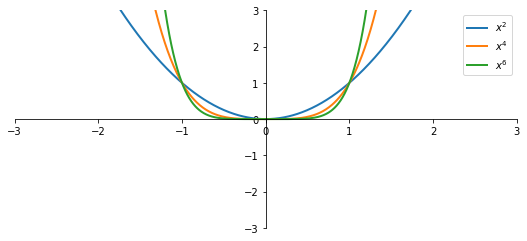
Radice di esponente pari

$${f(x)=\sqrt[2n]{x} = x^{{1\over 2n}},\quad n\in\mathbb{N},\quad n\geqslant 1}$$

Proprietà:

E' definita come l'inversa di $x^{2n}$ per $x\in\left[0,+\infty\right)$
(strettamente crescente, quindi iniettiva)
Dominio: $\left[0,+\infty\right)$
Codominio: $\left[0,+\infty\right)$
Strettamente crescente
Per $0\leqslant x \leqslant 1$ si ha $\sqrt[2n+2]{x} \geqslant \sqrt[2n]{x}$
Per $x \geqslant 1$ si ha $\sqrt[2n+2]{x} \leqslant \sqrt[2n]{x}$

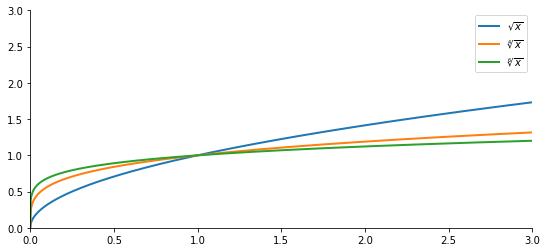
Radice di esponente pari

$${f(x)=\sqrt[2n]{x} = x^{{1\over 2n}},\quad n\in\mathbb{N},\quad n\geqslant 1}$$

Potenza con
esponente naturale dispari

$${f(x)=x^{2n+1},\quad n\in\mathbb{N}}$$

Proprietà:

Dispari
Dominio: $\mathbb{R}$
Codominio: $\mathbb{R}$
Iniettiva e suriettiva
Strettamente crescente
Per $0\leqslant x \leqslant 1$ si ha $x^{2n+3} \leqslant x^{2n+1}$
Per $x \geqslant 1$ si ha $x^{2n+3} \geqslant x^{2n+1}$

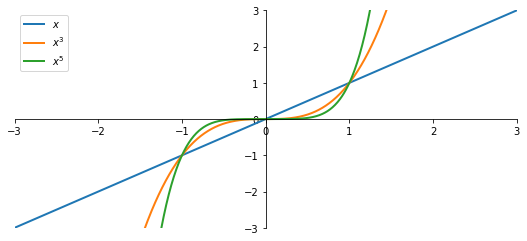
Potenza con esponente naturale dispari

$${f(x)=x^{2n+1},\quad n\in\mathbb{N}}$$

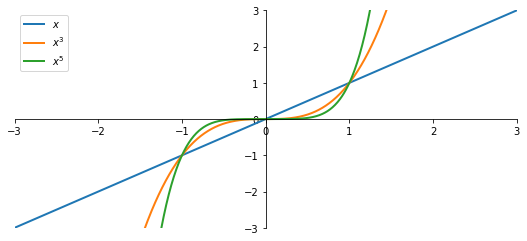
Radice di esponente dispari

$${f(x)=\sqrt[2n+1]{x} = x^{{1\over 2n+1}},\quad n\in\mathbb{N}}$$

Proprietà:

E' definita come l'inversa di $x^{2n+1}$
(strettamente crescente, quindi iniettiva)
Dominio: $\mathbb{R}$
Codominio: $\mathbb{R}$
Strettamente crescente
Per $0\leqslant x \leqslant 1$ si ha $\sqrt[2n+3]{x} \geqslant \sqrt[2n+1]{x}$
Per $x \geqslant 1$ si ha $\sqrt[2n+3]{x} \leqslant \sqrt[2n+1]{x}$

Radice di esponente dispari

$${f(x)=\sqrt[2n+1]{x} = x^{{1\over 2n+1}},\quad n\in\mathbb{N}}$$

Potenze pari e dispari

$${f(x) = x^n,\quad n\in\mathbb{N}}$$

Proprietà:

Per $0\leqslant x \leqslant 1$ si ha $x^{n+1} \leqslant x^{n}$
Per $x \geqslant 1$ si ha $x^{n+1} \geqslant x^{n}$

Radici pari e dispari

$${f(x) = \sqrt[n]{x},\quad n\in\mathbb{N}}$$

Proprietà:

Per $0\leqslant x \leqslant 1$ si ha $\sqrt[n+1]{x} \geqslant \sqrt[n]{x}$
Per $x \geqslant 1$ si ha $\sqrt[n+1]{x} \leqslant \sqrt[n]{x}$

Convenzione per le radici

Ci sono due convenzioni:

Convenzione della radice reale

Dominio per le radici pari: $\left[0,+\infty\right)$
Dominio per le radici dispari: $\mathbb{R}$

Qui ha senso scrivere $\sqrt[3]{-27}=-3$

Convenzione della radice principale

Dominio $\left[0,+\infty\right)$ per tutte le radici sia pari che dispari

Qui bisogna dare un interpretazione di $\sqrt[3]{-27}=3\sqrt[3]{-1}$ (richiede la conoscenza dei numeri complessi)

Noi useremo la seconda convenzione (radice principale)!

Potenza con esponente intero negativo pari

$${f(x) = x^{-n} = {1\over x^{n}},\quad n\in\mathbb{N},\ n\geqslant1}$$

Proprietà se $n$ è pari

$f(x)$ è pari
Dominio: $\mathbb{R} \setminus {0}$
Codominio: $(0,+\infty)$
Per $x\in(-\infty,0)$ è strettamente crescente
Per $x\in(0,+\infty)$ è strettamente decrescente

Potenza con esponente intero negativo dispari

$${f(x) = x^{-n} = {1\over x^{n}},\quad n\in\mathbb{N},\ n\geqslant1}$$

Proprietà se $n$ è dispari

$f(x)$ è dispari
Dominio $\mathbb{R} \setminus {0}$
Codominio: $\mathbb{R} \setminus {0}$
Per $x\in(-\infty,0)$ è strett. decrescente
Per $x\in(0,+\infty)$ è strett. decrescente

Potenze con esponente razionale

Avendo definito il dominio di tutte come $x\in\left[0,+\infty\right)$, risulta ben definito $$ f(x) = x^{{m\over n}},\quad m,\ n\in\mathbb{Z} $$ cioè $$x^{{m\over n}} = (x^{m})^{1\over n} = \left(x^{1\over n}\right)^{m}$$

Altrimenti, $x^{{m\over n}}$ produrrebbe risultati diversi di $x^{{\alpha m\over \alpha n}}$ con $\alpha\in\mathbb{N}$

Ad esempio, per $x<0$

$x^{{1\over 2}} = \sqrt{x}$ non è calcolabile (radice pari di un numero negativo)
$x^{{1\cdot 2\over 2\cdot 2}} = x^{{2\over 4}} = \sqrt[4]{x^2}$ è calcolabile

Proprietà delle potenze

Se $x,\ y > 0$ e $p,\ q \in\mathbb{Q}$ allora

$x^{p}>0$
$(x y)^{p} = x^{p} y^{p}$
$x^{p} x^{q} = x^{p+q}$
$x^{-p} = {1\over x^{p}}$
$x^{p}/x^{q} = x^{p-q}$
$(x^{p})^{q} = x^{pq}$
$(x/y)^{p} = x^{p} / y^{p}$

Se $p<q$ si ha:

se $x>1$ allora $x^p < x^q$
se $0 < x < 1$ allora $x^p > x^q$

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).