Funzioni elementari - parte 1

Obiettivo (corso Analisi Matematica 1)

Funzione segno
Parte intera e parte frazionaria
Funzione lineare
Valore assoluto
Funzione quadratica
Radice quadrata
Scomposizione parte positiva e negativa di una funzione

VIDEO

PDF

Funzione segno

$$f(x) = \operatorname {sign} x =\left\{{\begin{matrix}-1,& x<0\\0,& x=0\\1,& x>0\end{matrix}}\right.$$

Proprietà:

Non è né iniettiva né suriettiva
E' crescente
E' dispari
Non è periodica
Dominio: $\mathbb{R}$
Codominio: ${-1,0,1}$

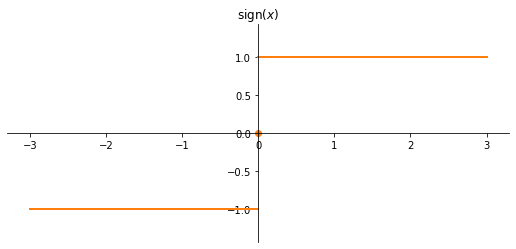
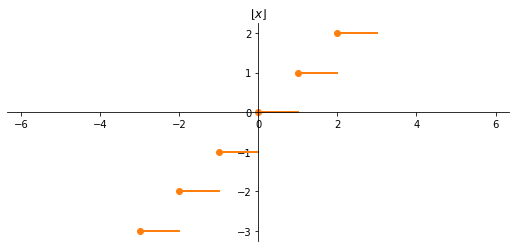
Funzione parte intera inferiore

$$f(x)=\lfloor x\rfloor = \max{{n\in\mathbb{Z}\colon n\leqslant x}}$$

Proprietà:

Non è né iniettiva né suriettiva
E' crescente
Non è né dispari né dispari
Non è periodica
E' costante in ogni intervallo del tipo $\left[n,n+1\right)$ con $n\in\mathbb{Z}$
Dominio: $\mathbb{R}$
Codominio: $\mathbb{Z}$

Funzione parte intera superiore

$$f(x)=\lceil x\rceil = \min{{n\in\mathbb{Z}\colon n\geqslant x}}$$

Proprietà:

Non è né iniettiva né suriettiva
E' crescente
Non è né dispari né dispari
Non è periodica
E' costante in ogni intervallo del tipo $\left(n,n+1\right]$ con $n\in\mathbb{Z}$
Dominio: $\mathbb{R}$
Codominio: $\mathbb{Z}$

Se $x\in\mathbb{Z}\implies\lceil x\rceil = \lfloor x\rfloor$
Se $x\in\mathbb{R}\setminus\mathbb{Z}\implies\lceil x\rceil = \lfloor x\rfloor + 1$

Funzione parte frazionaria (o mantissa)

$$f(x)= x - \lfloor x\rfloor$$

Proprietà:

Non è né iniettiva né suriettiva
E' crescente su ogni intervallo del tipo $\left[n,n+1\right)$ con $n\in\mathbb{Z}$, ma non su tutto il dominio
Non è né dispari né dispari
E' periodica di periodo 1
Dominio: $\mathbb{R}$
Codominio: $\left[0,1\right)$

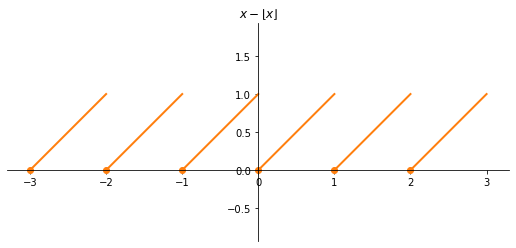
Funzione costante

$$f(x)=c, \quad c\in\mathbb{R}$$

Proprietà:

Se $c>0$ positiva
Se $c=0$ asse $x$
Se $c<0$ negativa
Dominio: $\mathbb{R}$
Codominio: ${c}$

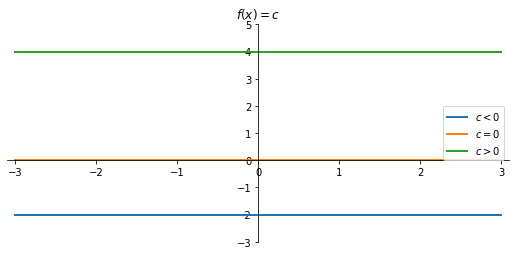
Funzione lineare / affine (retta)

$$f(x)=a x + b, \quad a\ne0$$

Proprietà:

Se $a>0$ retta crescente
Se $a<0$ retta decrescente
Se $b=0$ allora $y=ax$ passa per l'origine $(0,0)$
E' iniettiva e suriettiva
Dominio: $\mathbb{R}$
Codominio: $\mathbb{R}$

Valore assoluto

$$f(x)=|x| = \left\{{\begin{matrix}x,& x\geqslant0\\-x,& x<0\end{matrix}}\right.$$

Proprietà:

Funzione pari
Non è né iniettiva né suriettiva
Dominio: $\mathbb{R}$
Codominio: $\mathbb{R}^{+} = \left[0,+\infty\right)$

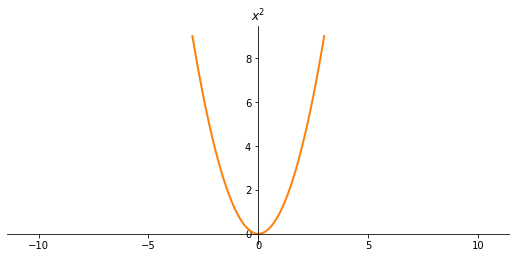
Funzione quadratica

$$f(x)=x^2$$

Proprietà:

Concava verso l'alto
Per $x=0 \implies f(0)=0$
(passa per l'origine)
Non è né iniettiva e né suriettiva

Dominio: $\mathbb{R}$
Codominio: $\mathbb{R}^{+} = \left[0,+\infty\right)$
Se $x\in\left(-\infty,0\right]$ è strett. decr.
Se $x\in \left[0,+\infty\right)$ è strett. cresc.

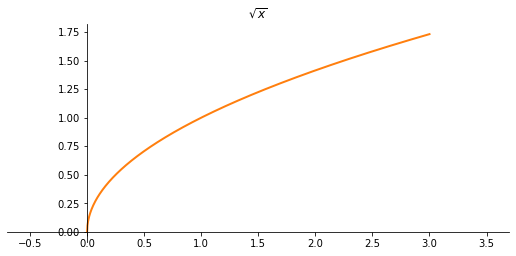
Funzione radice quadrata

$$f(x)=\sqrt{x}$$

Proprietà:

E' definita come l'inversa di $x^2$ per $x\in \left[0,+\infty\right)$
(strettamente crescente, quindi iniettiva)
Strettamente crescente
Dominio: $\left[0,+\infty\right)$
Codominio: $\mathbb{R}^{+} = \left[0,+\infty\right)$
$\sqrt{x^2} = |x|$

Ha senso scrivere: $\sqrt{4}=\pm2 \implies$ No!

Invece, ha senso scrivere: $\sqrt{4}=2$ e $\pm\sqrt{4}=\pm2$.

L' idea è che vogliamo una funzione ad un unico valore mentre ci sono due possibilità per definire $\sqrt{x}$ e quindi abbiamo scelto quella positiva (detta ramo principale)

Funzione parte positiva e negativa

Data una funzione $f(x)$ possiamo definire

parte positiva $f^{+}(x)= {|f(x)| + f(x)\over 2} \quad = \quad \max(f(x),0) \geqslant0$
parte negativa $f^{-}(x)= {|f(x)| - f(x)\over 2} \quad = \quad \max(-f(x),0) \geqslant0$

tale che $f(x) = f^{+}(x) - f^{-}(x)$

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).