Funzioni pari, dispari, periodiche e convesse
Obiettivo (corso Analisi Matematica 1)
- Funzione pari e funzione dispari
- Funzione periodica
- Definizione di funzione convessa
Funzione pari e dispari (definizione)
Sia $f\colon X\subseteq\mathbb{R}\to\mathbb{R}$ una funzione, si dice che $f(x)$
è pari sse ${f(x)=f(-x)}$ per ogni $x\in X$
è dispari sse ${f(x)=-f(-x)}$ per ogni $x\in X$
Proprietà
- Il grafico di una funzione pari è simmetrico rispetto alla retta delle ordinate $x=0$
- Il grafico di una funzione dispari è simmetrico rispetto all'origine $(0,0)$
- Se $f$ è pari allora non può essere iniettiva
- Il dominio di una funzione pari o dispari è simmetrico rispetto allo $0$
Esempio di funzione pari e dispari

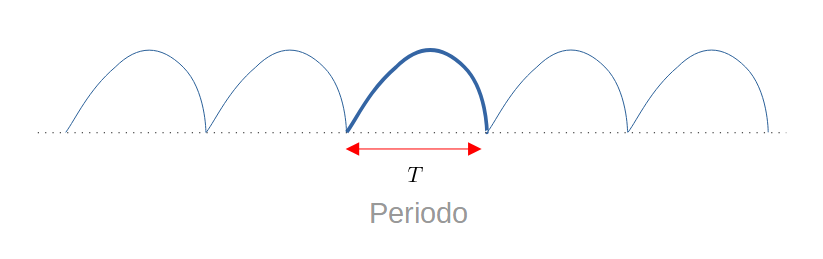
Funzioni periodiche (definizione)
Sia $f\colon X\subseteq\mathbb{R}\to\mathbb{R}$ una funzione e $T>0$, si dice che $f(x)$ è periodica sse
${f(x+T)=f(x)}$ per ogni $x\in X$
Il più piccolo $T$ che verifica l'uguaglianza è detto periodo
Proprietà
Se $f,g$ sono funzioni periodiche di periodo $T$ allora:
- il dominio non è limitato
- non è iniettiva
- è sufficiente studiare le proprietà in un periodo del tipo $[x_0, x_0+T)$ e poi applicare una traslazione di quest'ultimo intervallo parallelamente all'asse $x$
- $f(\alpha x)$ con $\alpha\ne0$ ha periodo $T/|\alpha|$
- $f+g$, $f\cdot g$ e $f/g$ hanno periodo $\leqslant T$
Se $g$ è periodica di periodo $T$ e $f$ qualunque allora $f(g(x))$ ha periodo $\leqslant T$
Esempi di funzioni periodiche
Esempio di somma con riduzione del periodo

Funzioni convesse (definizione)
Sia $I\subseteq\mathbb{R}$ un intervallo e $f\colon I \to \mathbb{R}$, $f$ si dice convessa sse per ogni $x_1,x_2\in I$ e per ogni $t\in [0,1]$ si ha che $${f((1-t)x_1+tx_2) \leqslant (1-t)f(x_1) + tf(x_2)}$$
$f$ è concava se $-f$ è convessa
Interpretazione grafica
- Combinazione convessa: $x(t) = (1-t)x_1+tx_2$
- Retta per i due punti $(x_1, f(x_1))$ e $(x_2, f(x_2))$: ${y - f(x_1)\over f(x_2) - f(x_1)} = {x - x_1\over x_2 - x_1}$
- Valutaz. retta in $x(t)$ è: $${y - f(x_1)\over f(x_2) - f(x_1)} = {(1-t)x_1+tx_2 - x_1\over x_2 - x_1} \ \implies y = t(f(x_2) - f(x_1)) + f(x_1) \ \implies y = (1-t)f(x_1) + t f(x_2)$$
- Convessa: il grafico della funzione sta "sotto" il grafico della retta
- La retta è sia concava che convessa
Interpretazione grafica

Esempio di funzione convessa
Mostrare che $x^2$ è convessa
Soluzione
Sia $x_1 < x_2$ dobbiamo dimostrare che
$$ ((1-t)x_1+tx_2)^2 \leqslant (1-t)x_1^2 + t x_2^2 \quad \forall t\in[0,1] $$
Si ha
$$ \begin{gathered} (1-t)^2 x_1^2 + t^2 x_2^2 + 2t(1-t) x_1 x_2 \leqslant (1-t)x_1^2 + t x_2^2 \\ (1-t)x_1^2(1-t-1) + tx_2^2(t-1) + 2t(1-t) x_1 x_2 \leqslant 0 \\ -t(1-t) x_1^2 - t(1-t)x_2^2 + 2t(1-t) x_1 x_2 \leqslant 0 \\ -t(1-t)(x_1^2+x_2^2-2x_1 x_2) \leqslant 0 \\ -t(1-t)(x_1-x_2)^2 \leqslant 0 \end{gathered} $$
Ricordando che $t\in[0,1]$ si ha che $-t\leqslant 0$, $1-t\geqslant0$ e $(x_1-x_2)^2\geqslant0$ da cui la diseguaglianza
Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).
