Definizione di funzione, f. iniettiva, f. suriettiva e inversa

Obiettivo (corso Analisi Matematica 1)

Definizione di funzione
Immagine / Contro-immagine / Dominio / Grafico
Funzione suriettiva
Funzione iniettiva
Funzione biiettiva
Funzione inversa
Inversa per via grafica

Definizione di funzione

Definizione
Dati due insiemi $X,Y\ne\emptyset$, si dice funzione da $X$ in $Y$ una relazione $f$ tale che

$\forall x\in X,\ \exists! y\in Y$ tale che $y=f(x)$

Nota:

Per relazione si intende un qualsiasi sottoinsieme del prodotto cartesiano $A\times B$
Quindi la funzione è un particolare sottoinsieme del prodotto cartesiano

Scritture alternative

$$ \begin{matrix} f:&X&\longrightarrow &Y\\ &x&\longmapsto &f(x) \end{matrix} $$

Esempio di funzione e di non funzione

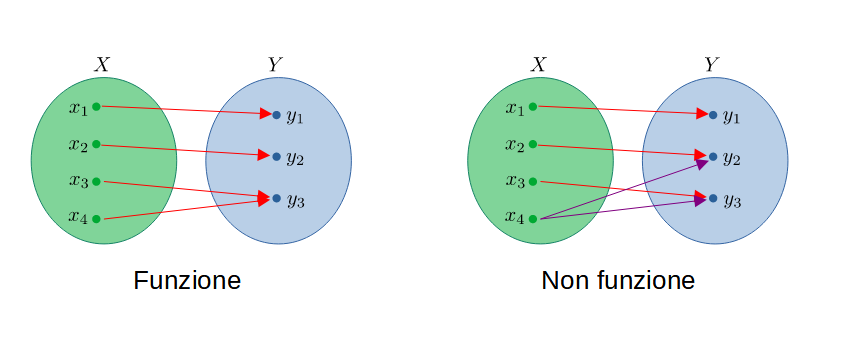
Altre definizioni inerenti le funzioni

Sia $f\colon X \to Y$, allora

$X$ dominio indicato con $\mathcal{D}(f)$
$Y$ codominio: indicato con $\mathcal{C}(f)$
Immagine di $f$: $$\mathcal{I}(f)={f(x)\colon x \in X} \subseteq Y$$
- se $C$ è un insieme $f(C)={f(c)\colon c\in C}\subseteq Y$
Contro-immagine di $S$ secondo $f$: $$f^{-1}(S)={x\in X \colon f(x)\in S}$$
Grafico di $f$: $$\mathcal{G}(f)={(x,f(x))\colon x\in X}\subseteq (X\times Y)$$

Esempio

Studiale le proprietà di $f(x)=x^2$

Soluzione

Dominio $\mathbb{R}$
Codominio $\mathbb{R}^{+}$ (numeri maggiori o uguali a zero)
Esempio di valutazione: $f(\pm 1)= 1$, $f(\pm2)= 4$
Contro-immagine di ${-1}$ è $f^{-1}({-1})=\emptyset$

Contro-immagine di ${1}$ è

$$f^{-1}({-1}) = {-1, 1}$$

Grafico di $f$

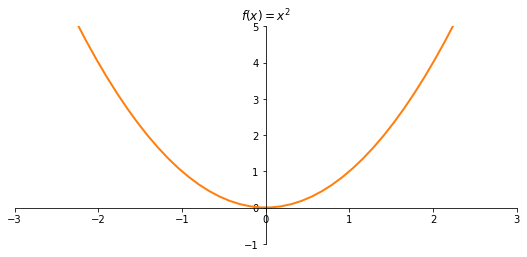
Funzione suriettiva

Definizione
Una funzione $f$ si dice suriettiva se ogni elemento del codominio è immagine di almeno un elemento del dominio

$\forall y \in Y, \exists x \in X$ tale che $f(x) = y$

E' equivalente a $\mathcal{I}(f)=Y$

Restrizione del codominio

E' sempre possibile restringere il codominio affinché $f$ sia suriettiva

Esempio

Sia $f(x)=x^2$, allora

$f$ non è suriettiva in $\mathbb{R}$, infatti $-1$ non è mappato
$f$ è suriettiva in $\mathbb{R}^{+}$

Funzione iniettiva

Definizione
Una funzione $f$ si dice iniettiva se associa, a elementi distinti del dominio, elementi distinti del codominio i.e.

$$\forall x,y\in X,\;\;x\neq y\implies f(x)\neq f(y)$$

Sono equivalenti:

$\forall x,y\in X,\;\;x\neq y\implies f(x)\neq f(y)$
$\forall x,y\in X,\;\;f(x)=f(y)\implies x=y$
$\forall y\in\mathcal{I}(f),\ \exists! x\in X$ tale che $y=f(x)$

Restrizione del dominio

E' sempre possibile restringere il dominio affinché $f$ sia iniettiva (in questo caso si cerca il dominio più grande possibile)

Esempio

Funzione biiettiva

Definizione
Una funzione si dice biiettiva se e solo se è contemporaneamente iniettiva e suriettiva, i.e. $$\forall y\in Y,\ \exists! x\in X\text{ tale che }y=f(x)$$

Esempio

La funzione $f \colon [0,+\infty]\to [0,+\infty]$ definita come $f(x)=x^2$ è iniettiva e suriettiva e quindi biiettiva

Funzioni somma, prodotto e rapporto

Siano $f_1\colon X_1 \to \mathbb{R}$ e $f_2\colon X_2 \to \mathbb{R}$ allora

somma: $(f_1+f_2)\colon (X_1 \cap X_2)\to \mathbb{R}$ come $f_1(x)+f_1(x)$
- dominio $\mathcal{D}(f_1+f_2)=\mathcal{D}(f_1)\cap\mathcal{D}(f_2)$

prodotto: $(f_1 \cdot f_2)\colon (X_1 \cap X_2)\to \mathbb{R}$ come $f_1(x) \cdot f_1(x)$
- dominio $\mathcal{D}(f_1\cdot f_2)=\mathcal{D}(f_1)\cap\mathcal{D}(f_2)$

rapporto: $(f_1 / f_2)\colon (X_1 \cap {x\in X_2\colon f_2(x)\ne0})\to \mathbb{R}$ come $f_1(x) \cdot f_1(x)$
- dominio $\mathcal{D}(f_1 / f_2)=\mathcal{D}(f_1)\cap\mathcal{D}(f_2) \cap {x\in\mathcal{D}(f_2)\colon f_2(x)\ne0}$

Funzione composta

Siano $g\colon X \to Y$ e $f\colon Y \to Z$ allora la funzione composta è definita come $f \circ g = f(g(x))$

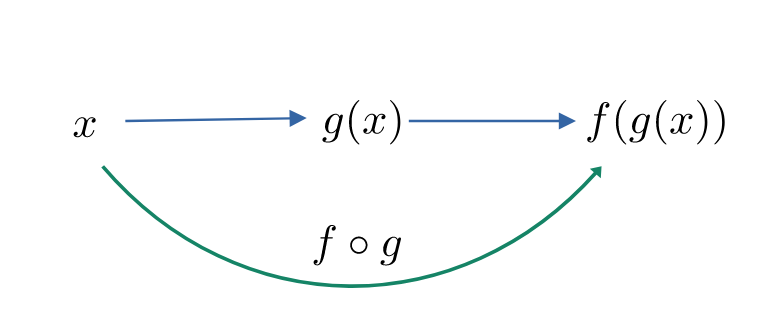
Esempio

Sia $f\colon\mathbb{R}\to\mathbb{R}$ tale che $$x\mapsto x+1$$ e $g\colon\mathbb{R}\to\mathbb{R}$ tale che $$x\mapsto x^2$$ allora

$f(g(x)) = f(x^2) = x^2+1$

$g(f(x)) = g(x+1) = (x+1)^2$

Proprietà

$f \circ g \ne g \circ f$
La composizione di due funzioni iniettive è iniettiva
La composizione di due funzioni biiettive è biiettiva

Esercizio

Dimostrare che se $f$ è inittiva e $g$ è inittiva, allora $f\circ g$ è inittiva

Dimostrazione

Dati due numeri $x_1,\ x_2\in \mathcal{D}(g)$ tali che $x_1\ne x_2$ si ha

$$ y_1 = g(x_1) \ne g(x_2)=y_2 $$

in quanto $g$ è iniettiva.

Ora, dal momento che $y_1\ne y_2$ e $f$ è inittiva segue che

$$ f(y_1)\ne f(y_2) \;\iff\; f(g(x_1))\ne f(g(x_2)) $$

dimostrando che la composione $f\circ g$ è inittiva.

Funzione inversa

Una funzione $f\colon X\to Y$ si dice invertibile se esiste una funzione $g\colon Y\to X$ tale che

$g(f(x))=x$ per ogni $x\in X$, e

$f(g(y))=y$ per ogni $y\in Y$

L'inversa di una funzione $f$ viene indica con $f^{-1}$

Nota

Una funzione suriettiva garantisce che tutti i punti del codominio siano raggiungibili
Una funzione iniettiva garantisce la corrispondenza uno a uno tra dominio e codominio
E' sempre possibile restringere il dominio e il codominio di una funzione in modo tale da renderla iniettiva e suriettiva (in questo caso si cerca il dominio più grande possibile)

Grafico dell'inversa

Sia $f$ una funzione biiettiva e $f^{-1}$ la sua inversa, allora il grafico di $f$ è legato al grafico di $f^{-1}$ dalla relazione $$ \mathcal{G}(f^{-1})={(y,f^{-1}(y))\colon y\in f(X)} = {(f(x),x)\colon x\in X} $$ ovvero $(x,y)\in\mathcal{G}(f)\leftrightarrow (y,x)\in\mathcal{G}(f^{-1})$ i.e si dispongono in modo simmetrico rispetto alla retta bisettrice del I-III quadrante

Esempio di inversa per via grafica

Dato il grafico $f$ derivare il grafico della sua inversa $f^{-1}$

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).