Primi esercizi sul maggiorante, massimo e estremo superiore
Indice esercizi (corso Analisi Matematica 1)
Determinare, se esistono, $\sup A$, $\inf A$, $\max A$ e $\min A$ di
- $A=\left\{{2-n\over n+1}\colon n\in\mathbb{N}\right\}$
- $A=\left\{{(-1)^n\over n}\colon n\in\mathbb{N}, n>0\right\}$
- $A=\left\{n^2+4n-1\colon n\in\mathbb{N}\right\}$
- $A=\left\{{2n\over n^2+1}\colon n\in\mathbb{Z}\right\}$
- $A=\left\{{1\over n^2}-{1\over n}\colon n\in\mathbb{N}, n>0\right\}$
Esercizi
Esercizio 1
Determinare, se esistono, ${\sup A}$, ${\inf A}$, ${\max A}$ e ${\min A}$ di
$${A=\left\{{2-n\over n+1}\colon n\in\mathbb{N}\right\}}$$
Soluzione
Osserviamo che $$ {2-n\over n+1} = {-(n+1-2-1)\over n+1} = -1 + 3{1\over n+1} $$ e $$ 0 < {1\over n+1} \leqslant 1 \quad \forall n\in\mathbb{N} $$ Per $n=0$ si ha ${1\over n+1}=1$
Quindi,
- $\sup A = -1+3 = 2 = \max A$
- $\inf A = -1$ (non è mai assunto)
Esercizio 1 (visualizzazione grafica)
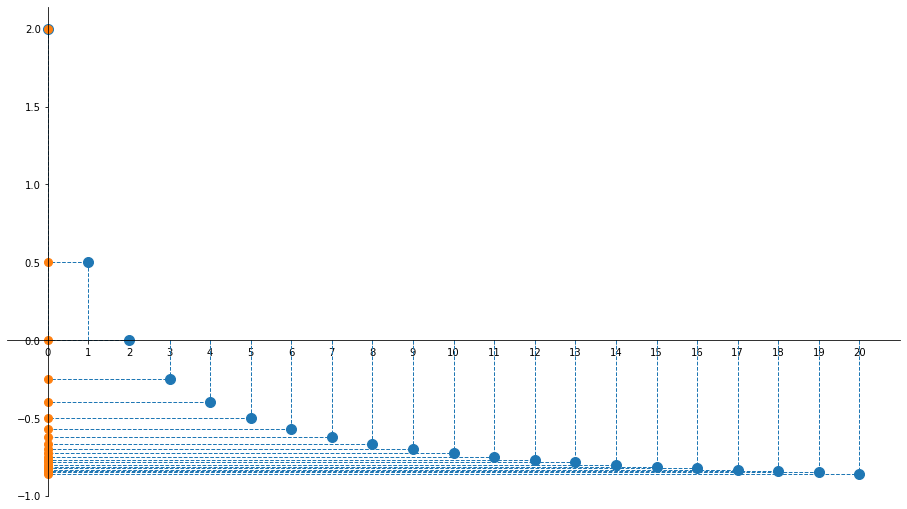
Esercizio 2
Determinare, se esistono, ${\sup A}$, ${\inf A}$, ${\max A}$ e ${\min A}$ di
$${A=\left\{{(-1)^n\over n}\colon n\in\mathbb{N}, n>0\right\}}$$
Soluzione
Osserviamo che
- Se $n$ è pari ${(-1)^n\over n} = {1\over n} \leqslant {1\over2}$ (2 è il primo numero pari)
- Se $n$ è dispari ${(-1)^n\over n} = -{1\over n} \geqslant -1$ (1 è il primo numero dispari)
Quindi
- $\max A = \sup A = {1\over2}$
- $\min A = \inf A = -1$
Esercizio 2 (visualizzazione grafica)
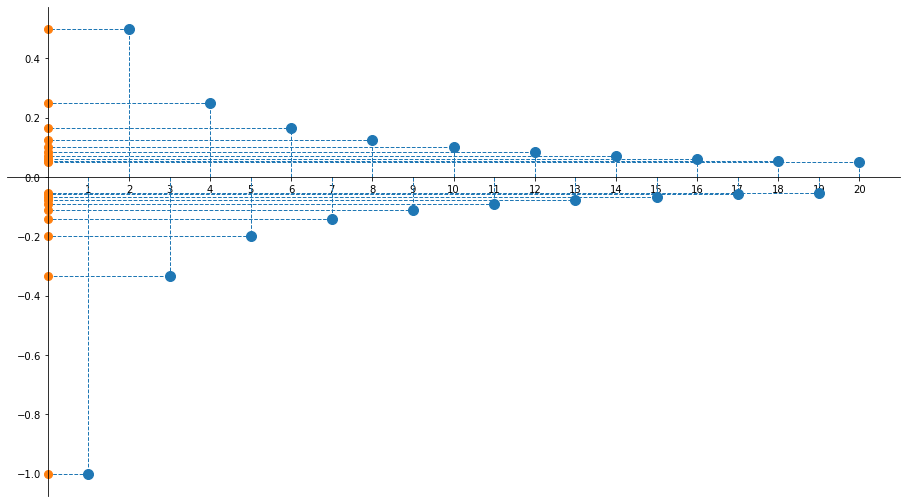
Esercizio 3
Determinare, se esistono, ${\sup A}$, ${\inf A}$, ${\max A}$ e ${\min A}$ di
$${A=\left\{n^2+4n-1\colon n\in\mathbb{N}\right\}}$$
Soluzione
(Andate a vedere come si disegna una parabola)
Il polinomio $n^2+4n-1$ è crescente per $n\geqslant0$ quindi il suo minimo è raggiunto per $n=0$ e quindi $\min A = \inf A = -1$
Il polinomio $n^2+4n-1$ non è limitato superiormente, quindi $\sup A = +\infty$ (non esiste massimo)
Esercizio 3 (visualizzazione grafica)
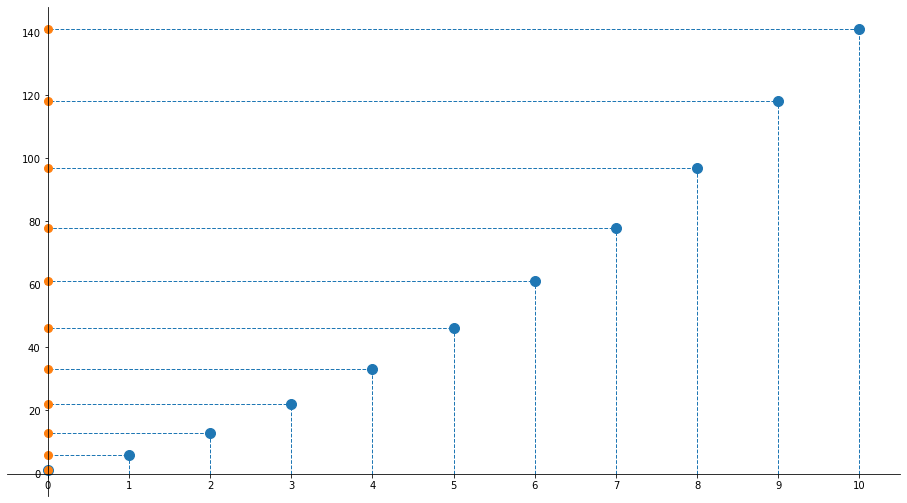
Esercizio 4
Determinare, se esiste, ${\sup A}$, ${\inf A}$, ${\max A}$ e ${\min A}$ di
$${A=\left\{{2n\over n^2+1}\colon n\in\mathbb{Z}\right\}}$$
Soluzione
Si ha
- per $n\geqslant0$ si ha
- ${2n\over n^2+1}\geqslant0$ (termini positivi)
- ${2n\over n^2+1}\leqslant1$ infatti ${2n \leqslant n^2+1} \quad \iff \quad n^2-2n+1\geqslant 0 \quad \iff \quad (n-1)^2 \geqslant 0$
- per $n=0 \implies {2n\over n^2+1}=0$ e per $n=1 \implies {2n\over n^2+1}=1$
- per $n\leqslant0$ si ha
- ${2n\over n^2+1}\leqslant0$ (numeratore negativo, denominatore positivo)
- ${2n\over n^2+1}\geqslant-1$ infatti ${2n \geqslant -(n^2+1)} \quad \iff \quad n^2+2n+1\geqslant 0 \quad \iff \quad (n+1)^2 \geqslant 0$
- per $n=0 \implies {2n\over n^2+1}=0$ e per $n=-1 \implies {2n\over n^2+1}=-1$
Quindi
- $\min A = \inf A = -1$
- $\max A = \sup A = 1$
Esercizio 4 (visualizzazione grafica)
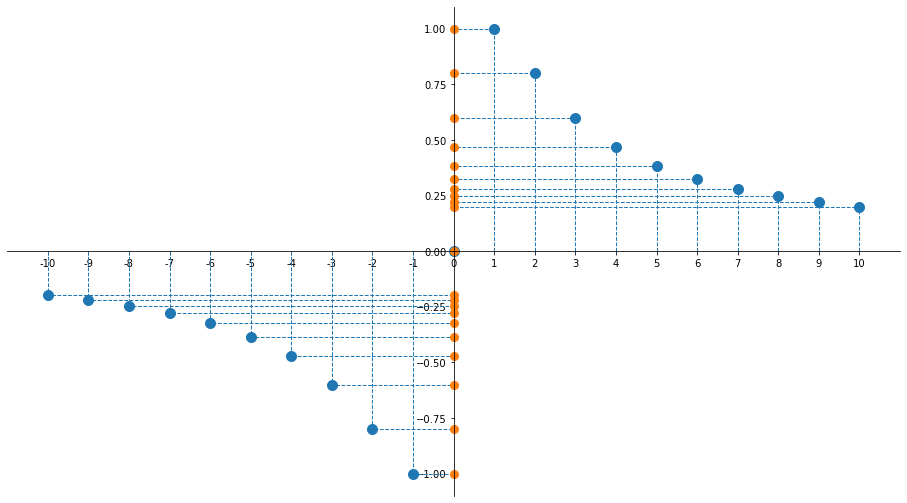
Esercizio 5
Determinare, se esistono, ${\sup A}$, ${\inf A}$, ${\max A}$ e ${\min A}$ di
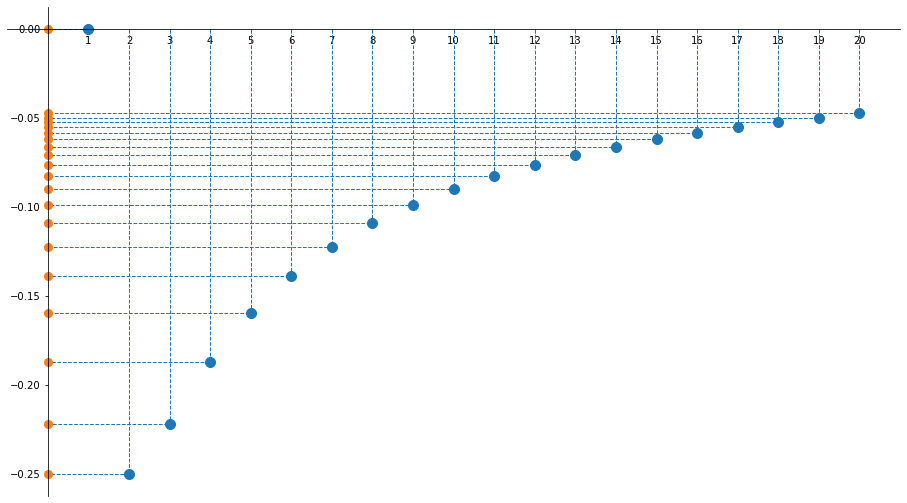
$${A=\left\{{1\over n^2}-{1\over n}\colon n\in\mathbb{N}, n>0\right\}}$$
Soluzione
Osserviamo che $${1\over n^2}-{1\over n}={1-n\over n^2}$$ e per $n\in\mathbb{N}$, con $n>0$ è $${1-n\over n^2}\leqslant0\quad (1-n\leqslant0)$$
Per $n=1$ si ha ${1-n\over n^2}=0$, quindi $$\max A = \sup A = 0$$
Proviamo a risolvere la seguente disequazione ${1-n\over n^2}\geqslant -\alpha$ con $\alpha>0$
Questa è equivalente a $1-n\geqslant -\alpha n^2 \quad \iff \quad \alpha n^2 - n +1 \geqslant 0$
Scegliendo $\alpha={1\over 2}$, si può completare il quadrato e si ottiene che $\left({n\over2}-1\right)^2\geqslant 0$
Quindi $-{1\over 2}$ è un minorante per $A$
Punto chiave: è una successione crescente a partire da un certo $n_0$
Infatti $$ \left({1\over(n+1)^2}-{1\over n+1}\right) > \left({1\over n^2}-{1\over n}\right) $$ $$ {1\over(n+1)^2}-{1\over n^2} > {1\over n+1}-{1\over n} \quad \iff \quad {n^2-(n+1)^2\over n^2(n+1)^2} > {n-(n+1)\over n(n+1)} $$ $$ {-2n-1} > -n(n+1) \quad \iff \quad n^2 -n -1 > 0 \quad \iff \quad n(n-1) > 1 $$ che risulta vera per $n\geqslant 2$
Valutando l'espressione per $n=1, 2$ si vede che il minimo è ottenuto per $n=2$ e vale $-{1\over4}$
Quindi, $$\min A = \inf A = -{1\over 4}$$
Esercizio 5 (visualizzazione grafica)
Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).
