Maggiorante, massimo ed estremo superiore

Obiettivo (corso Analisi Matematica 1)

Maggiorante e minorante
Massimo e minimo
Estremo superiore e estremo inferiore
Interpretazione grafica della successione

Maggiorante (risp. minorante)

Definizione
Sia $X$ un insieme ordinato sia $A \subseteq X$ non vuoto.
Un elemento $k$ di $X$ è un maggiorante (risp. minorante) di $A$ se

$k$ è confrontabile con ogni elemento di $A$

$\forall x \in A \colon x \preceq k$ (risp. $x \succeq k$)

Nota:

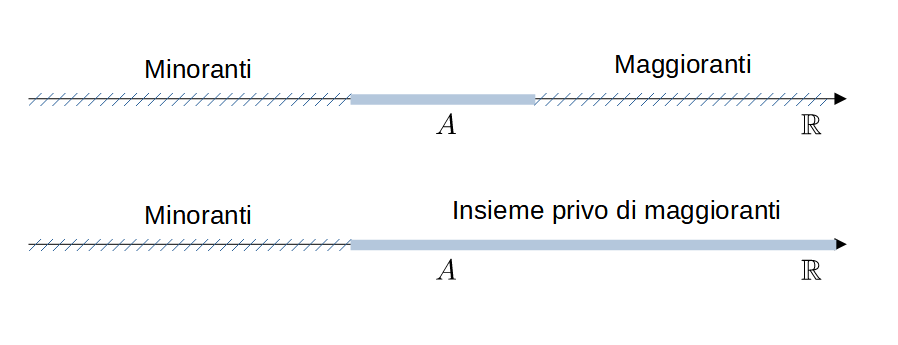
$A$ può non avere maggioranti, ne può avere uno solo o più di uno

Esempio

Se $A\subseteq\mathbb{R}$, $x$ è un maggiorante di $A$ se e solo se $a\leqslant x$ per ogni $a\in A$
Se $A\subseteq\mathbb{R}$, $x$ è un minorante di $A$ se e solo se $a\geqslant x$ per ogni $a\in A$

Altre definizioni

Se esiste almeno un maggiorante (minorante) l'insieme viene detto limitato superiormente (inferiormente)

Si dice limitato se è limitato sia superiormente che inferiormente

Massimo (risp. minimo)

Definizione
Sia $X$ un insieme ordinato sia $A \subseteq X$ non vuoto.
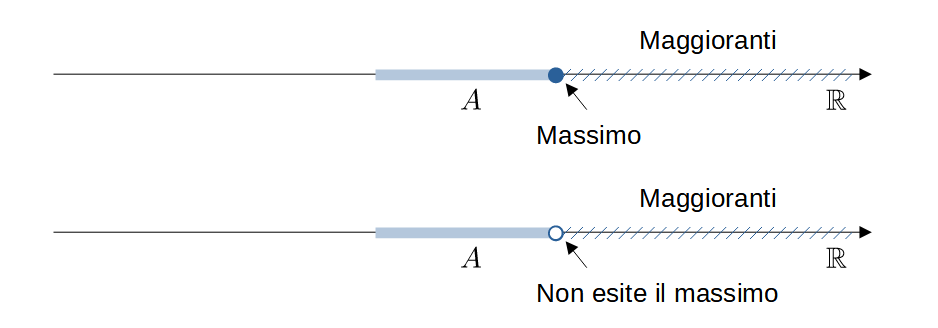
Un elemento $m$ di $X$ si dice massimo (risp. minimo) di $A$, $\max A$ (risp. $\min A$) se:

$m\in A$

$m$ è un maggiorante (risp. minorante) di $A$

Nota:

Non tutti gli insiemi sono dotati di massimo o di minimo
Il massimo (o il minimo) di $A$ se esiste è unico

Estremo superiore (risp. inferiore)

Definizione
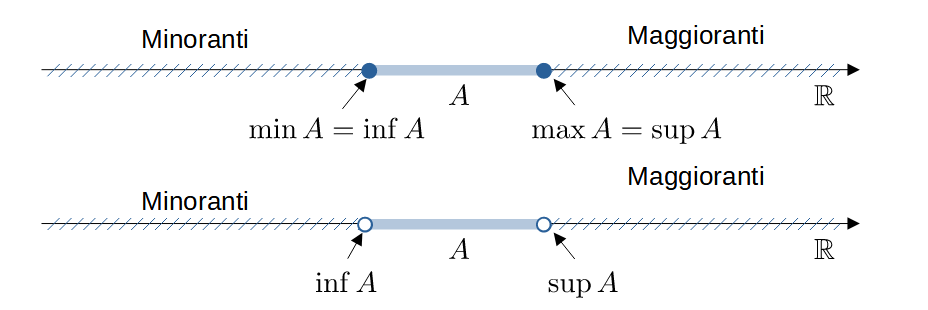
$\sup A$ (risp. $\inf A$) è il minimo (massimo) dei maggioranti (minoranti) di $A$, se esiste

Si ha

L'estremo superiore (risp. inferiore) se esiste è unico
Se $m$ è il massimo (risp. minimo) di $A$ esso coincide con $\sup A$ (risp. $\inf A$)
Se $A$ non è superiormente (risp. inferiormente) limitato scriveremo $\sup A = +\infty$ (risp. $\inf A = -\infty$)
$A$ può essere limitato superiormente (risp. inferiormente) e non ammettere massimo (risp. minimo)

Esempi

Esempio 1

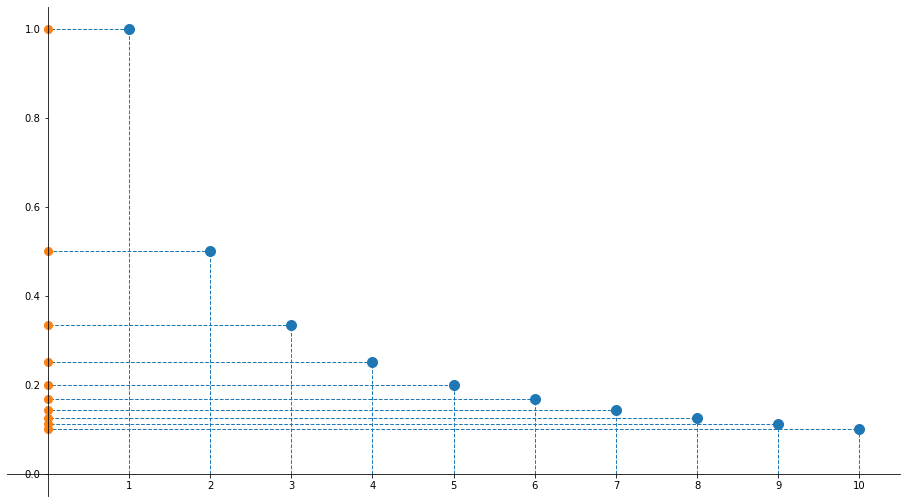
Determinare, se esiste, $\sup A$, $\inf A$, ${\max A}$ e ${\min A}$ di

$${A=\left\{{1\over n}\colon n\in\mathbb{N}, n\geqslant1\right\}}$$

Soluzione

Si ha

da ${1\over n}\geqslant0$ si ha che $0$ è un minorante di $A$ con $\inf A=0$
da ${1\over n}\leqslant1$ si ha che $1$ è un maggiorante di $A$ con $\sup A=1$
$\max A = 1$ è il massimo di $A$ (assunto per $n=1$)
$0$ non è un minimo di $A$ in quanto non viene mai raggiunto

Esempio 1 (interpretazione grafica della successione)

Esempio 2

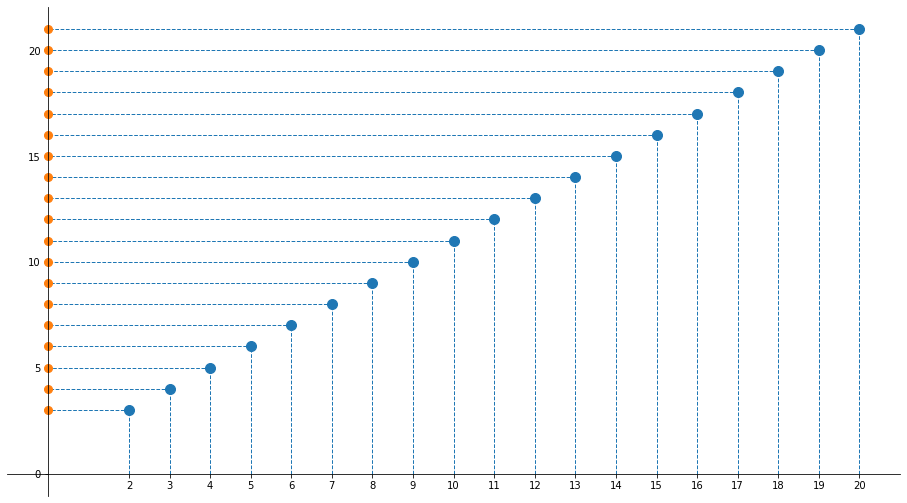
Determinare, se esiste, ${\sup A}$, ${\inf A}$, ${\max A}$ e ${\min A}$ di

$${A=\left\{{1-n^2\over 1-n}\colon n\in\mathbb{N}, n\geqslant2\right\}}$$

Soluzione

Si ha

${1-n^2\over 1-n} = {(1-n)(1+n)\over 1-n} = 1+n$
$\inf A = 1+2= 3 = \min A$
$\sup A = +\infty$

Esempio 2 (interpretazione grafica della successione)

Esempio 3

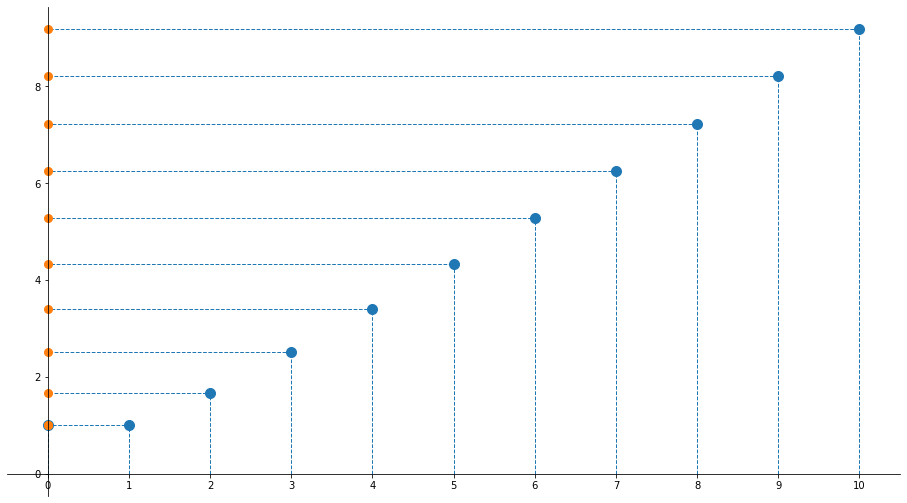
Determinare, se esiste, ${\sup A}$, ${\inf A}$, ${\max A}$ e ${\min A}$ di

$${A=\left\{{n^2+1\over n+1}\colon n\in\mathbb{N}\right\}}$$

Soluzione

Si ha

${n^2+1\over n+1} = {(n+1)(n-1)+2\over n+1} = n-1+{2\over n+1}$
$\sup A = +\infty$
E' inferiormente limitato in quanto sia $n-1$ che ${2\over n+1}$ sono inf. limit.
Da ${2\over n+1} < 1$ per $n>1$ cioè per $n\geqslant 2$ si ha che (valutazione per $n=0$ e $n=1$) $\min A = 1$

Esempio 3 (interpretazione grafica della successione)

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).