Relazioni insiemistiche

Obiettivo (corso Analisi Matematica 1)

• Prodotto cartesiano
• Relazioni d'ordine
• Relazioni di equivalenza

Prodotto cartesiano

Definizione
$$A \times B = {(x,y) \colon x\in A,\ y\in B}$$

Il prodotto cartesiano $A \times B$ è l'insieme di tutte le coppie ordinate $(x, y)$ con con $x\in A$ e $y\in B$

Nota:

• $A \times B \not = B \times A$

Esempio

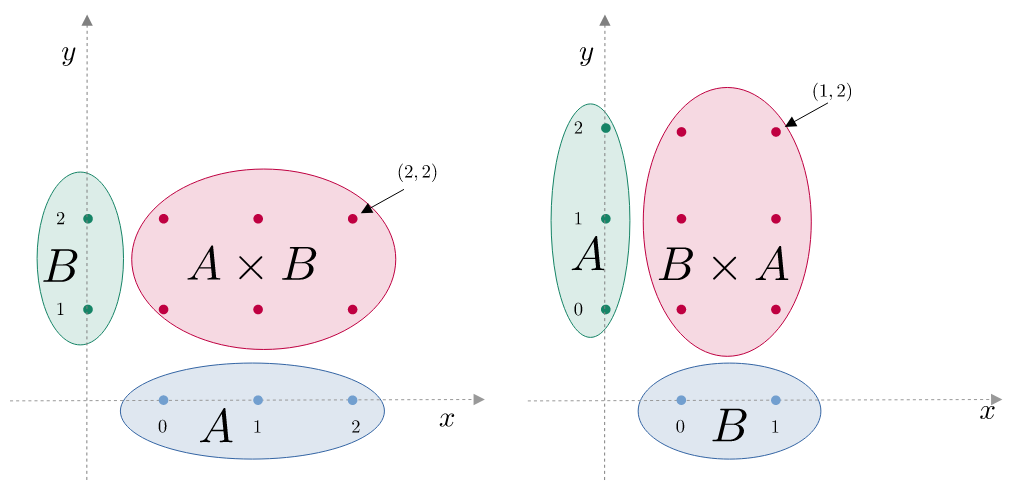
Se $A={0,\ 1,\ 2}$ e $B = {1,\ 2}$ allora

• $A \times B = {(0,1),(0,2),(1,1),(1,2),(2,1),(2,2)}$
• $B \times A = {(1,0),(1,1),(1,2),(2,0),(2,1),(2,2)}$

Relazioni notevoli

Le relazioni formalizziamo i concetti di

• equivalenza

• e di ordinamento

• sono alla base della definizione di funzione (che vedremo più avanti)

Definizione di relazione
Una relazione $\mathcal{R}$ tra due insieme $A$ e $B$, indicata con $A\mathcal{R}B$, è un qualunque sottoinsieme del prodotto cartesiano $A\times B$, i.e.
$a\in A$ è in relazione con $b\in B$ sse $(a,b)\in\mathcal{R}$

Relazione di equivalenza

$\mathcal{R}$ è una relazione di equivalenza in $A$ e la indicheremo con $a \approx b$ se verifica le proprietà:

1. riflessiva: $\forall a \in A \colon a \approx a$
2. simmetrica: $\forall a,b \in A,\ (a \approx b) \implies (b \approx a)$
3. transitiva: $\forall a,b,c \in A \colon (a \approx b) \land (b \approx c) \implies a \approx c$

Esempio

Esempi di relazioni di equivalenza sono:

• nelle frazioni, l'uguale a, ad esempio ${1\over2}={2\over4}=\ldots$
• la misura degli angoli (sono congruenti modulo $360^{\circ}=2\pi$)
  • $0^{\circ} = 360^{\circ} = -360^{\circ} = 720^{\circ} = \ldots$
• il parallelismo tra rette nello spazio
• la similitudine tra triangoli

Partizioni / classi di equivalenza

Le relazioni di equivalenza definiscono delle partizioni o classi di equivalenza e si indica con $[a]_{\mathcal{R}}={b\in A\colon a\mathcal{R}b}$

Ad esempio, la frazione ${1\over 2}$ (numeratore e denominatore primi tra loro) si può vedere come rappresentante delle infinite frazioni $$ {1\over 2} = {2\over 4} = {3\over 6} = {4\over 8} = \ldots $$

Quindi l'elemento ${1\over2}$ è il rappresentante principale di tale classe

Importante

Perché le relazioni di equivalenza sono importanti?

• L'uso di una relazione di equivalenza permette di decomporre l'insieme in sottoinsiemi disgiunti detti partizioni di equivalenza

• Se dimostriamo un teorema per un elemento della classe allora vale per tutti gli elementi della stessa classe

Ad esempio: il teorema di Pitagora si applicata a tutti i triangoli rettangoli e la condizione di essere un traingolo rettagolo o meno forma una classe di equivalenza

Relazione d'ordine

$\mathcal{R}$ è una relazione d'ordine in $A$ e la indicheremo con $a \preceq b$ ($a$ precede $b$) se verifica le proprietà:

1. riflessiva: $\forall a \in A \colon a \preceq a$
2. antisimmetrica: $\forall a,b \in A, (a \preceq b) \land (b \preceq a) \implies a = b$
3. transitiva: $\forall a,b,c \in A, (a \preceq b) \land (b \preceq c) \implies a \preceq c$

Se, presi due elementi $a$ e $b$ in $A$, possiamo stabilire che $a \preceq b$ oppure $b \preceq a$ (dicotomia) allora l'ordinamento si dirà totale, altrimenti parziale

Useremo il simbolo $\leqslant$ per gli insiemi numerici

Altre relazione d'ordine

Da una relazione d'ordine $\preceq$ su $A$ possiamo definire le seguenti relazioni:

• $a \succeq b$ sse $b \preceq a$ ($a$ segue o è uguale a $b$ se $b$ precede o è uguale a $a$)
• $a \prec b$ sse $a \preceq b$ e $a \ne b$
• $a \succ b$ sse $b \prec a$

Esempio sui numeri naturali

La relazione $\leqslant$ nell'insieme dei numeri reali $\mathbb{N}$ si identifica con l'insieme $${(x,y) \in \mathbb{N} \times \mathbb{N} \colon x \leqslant y}$$

E' una relazione d'ordine, infatti:

• riflessiva: $n\leqslant n$ per ogni $n\in\mathbb{N}$
• antisimmetrica: $\forall m,n \in \mathbb{N}, (m \leqslant n) \land (n \leqslant m) \implies m = n$
• transitiva: $\forall m,n,p \in \mathbb{N}, (m \leqslant n) \land (n \leqslant p) \implies m \leqslant p$
• dicotomia: presi due elementi li possiamo sempre confrontare

Quindi $\mathbb{N}$ è totalmente ordinato

Nota:

• La relazione $<$ non è una relazione d'ordine (non è riflessiva)
• Si può dimostrare che $\mathbb{R}$ è dotato di un ordinamento totale $\leqslant$

Curiosità

• Il padre della teoria degli insiemi è: Cantor (1845 - 1918)

• Cantor capì che gli insiemi infiniti potevano avere due tipi di cardinalità (numerabile e più che numerabile)

• Dimostrò che l'insieme di tutti i numeri razionali è numerabile mentre l'insieme dei numeri reali è più che numerabile

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).