Esercizi sugli insiemi

Indice esempi (corso Analisi Matematica 1)

1. $A \subseteq B \quad\iff\quad B^{c}\subseteq A^{c}$
2. $(A\cup B)^{c} \;=\; A^{c} \cap B^{c}$ (legge di De Morgan)
3. $A\ \Delta\ B \;=\; (A\cup B) \setminus (A\cap B)$
4. $A \;=\; (A\cap B) \;\cup\; (A\setminus B)$
5. $A\setminus (B \setminus C) \;=\; (A\setminus B) \;\cup\; (A\cap C)$

Esempi

Esempio 1

Dimostrare che $$A \subseteq B \quad\iff\quad B^{c}\subseteq A^{c}$$

Dimostrazione ⇒:

Da $A \subseteq B$ se $x\in B^{c} \implies x\not\in B \implies x \not\in A \implies x\in A^c$

Quindi, se $x\in B^{c}$ allora $x\in A^{c}$

Dimostrazione ⇐:

Da $B^{c}\subseteq A^{c}$ se $x\in A \implies x\not\in A^{c} \implies x \not\in B^{c} \implies x\in B$

Quindi, se $x\in A$ allora $x\in B$

Esempio 2

Dati due insiemi $A$ e $B$, dimostrare che $$(A\cup B)^{c} \;=\; A^{c} \cap B^{c}$$ (legge di De Morgan)

Dimostrazione

$$\begin{aligned} x\in(A\cup B)^{c}&\iff x \not\in (A\cup B) \\ &\iff x \not\in A \;\land\; x \not\in B\\ &\iff x \in A^{c} \;\land\; x \in B^{c}\\ &\iff x \in A^{c} \cap B^{c} \end{aligned}$$

Esempio 3

Dimostrare che $$A\ \Delta\ B = (A\cup B) \setminus (A\cap B)$$

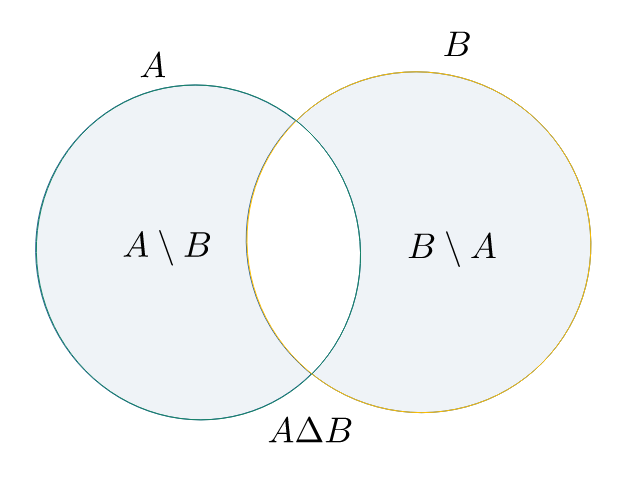
Esempio 3

Dimostrare che $$A\ \Delta\ B = (A\cup B) \setminus (A\cap B)$$

Ricordiamo

• $A\ \Delta\ B = (A\setminus B) \;\cup\; (B\setminus A)$
• differenza come intersezione: $A\setminus B=A\cap B^c$
• De Morgan intersezione: $(A \cap B)^{c} = A^{c} \cup B^{c}$
• distributiva: $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$

Dimostrazione

$$\begin{aligned} (A\cup B)\setminus(A\cap B) &=(A\cup B) \;\cap\; (A\cap B)^{c}\\ &=(A\cup B) \;\cap\; (A^{c}\cup B^{c})\\ &=((A\cup B)\cap A^{c}) \;\cup\; ((A\cup B)\cap B^{c})\\ &=(B\cap A^{c}) \;\cup\; (A\cap B^{c})\\ &=(B\setminus A) \;\cup\; (A\setminus B) \\ &= A\ \Delta\ B \end{aligned}$$

Esempio 4

Dimostrare che, per ogni $A$ e $B$ si ha $$A \;=\; (A\cap B) \;\cup\; (A\setminus B)$$

Dimostrazione

Provate voi con le proprietà distributive dell'unione e dell'intersezione

$$ A \;=\; A\cap U \;=\; A \;\cap\; (B \cup B^c) \;=\; (A \cap B) \;\cup\; (A \cap B^c) \;=\; (A \cap B) \;\cup\; (A \setminus B) $$

Esempio 5

Dimostrare che $$A \setminus (B \setminus C) \;=\; (A\setminus B) \;\cup\; (A\cap C)$$

. . .

Dimostrazione

$$\begin{aligned} A\setminus (B \setminus C) &= A \;\setminus\; (B \cap C^c)\\ &= A \;\cap\; (B \cap C^c)^c\\ &= A \;\cap\; (B^c \cup C)\\ &= (A \cap B^c) \;\cup\; (A\cap C)\\ &= (A \setminus B) \;\cup\; (A\cap C)\\ \end{aligned}$$

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).