Introduzione agli insiemi

Obiettivo (corso Analisi Matematica 1)

• Definizione di insieme
• Sottoinsieme / contenuo
• Unione
• Intersezione
• Differenza e differenza simmetrica
• Complementarietà
• Proprietà insiemistiche

Definizione
(un po' vaga ma va bene così)

Insieme: una collezione di oggetti detti elementi

Sinonimi: collezione / famiglia / classe / aggregato

Come descrivere un insieme

• per elencazione: $A = {x, y, z, \ldots}$
  • ad esempio: $A = {0,\ 1,\ 2,\ 3,\ 4,\ 5 }$

• per definizione: $A = {x \in \mathcal{U} \colon P(x) }$ (sono gli elementi di $\mathcal{U}$ tali che il predicato $P$ è vero)
  • ad esempio: $A = {x \in \mathbb{N} \colon 6 \leqslant x \leqslant 10 } = {6,\ 7,\ 8,\ 9,\ 10 }$

Graficamente gli insiemi si rappresentazione attraverso i Diagrammi di Venn

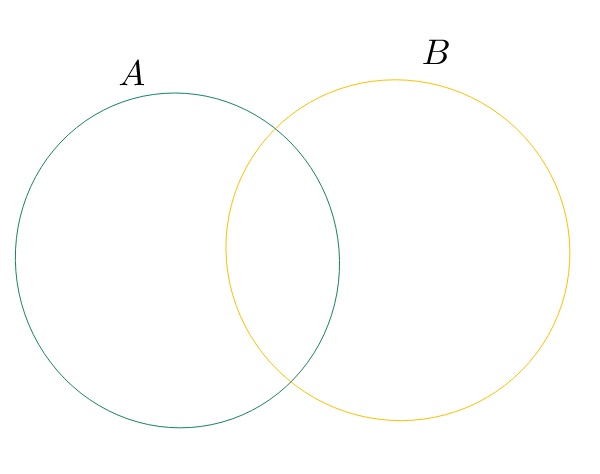
Notazione

• $x \in A$: $x$ appartiene ad $A$ (o $x$ è un elemento di $A$)

• $x \not\in A$: $x$ non appartiene ad $A$

• $\emptyset$: l'insieme vuoto

• Cardinalità di un insieme ovvero il numero dei suoi elementi (si indica con $|A|$)

Sottoinsieme / contenuo: $A \subseteq B$ o $B \supseteq A$

Se $A$, $B$ sono insiemi, $A$ è sottoinsieme di $B$ se ogni elemento di $A$ è anche elemento di $B$ $$A \subseteq B \quad \iff \quad \forall x \in A \colon x \in B$$

Nota:

• $A \subseteq B$ si legge $A$ è contenuto in $B$
• $B \supseteq A$ si legge $B$ contiene $A$
• $\emptyset \subseteq A$
• $A \subseteq A$

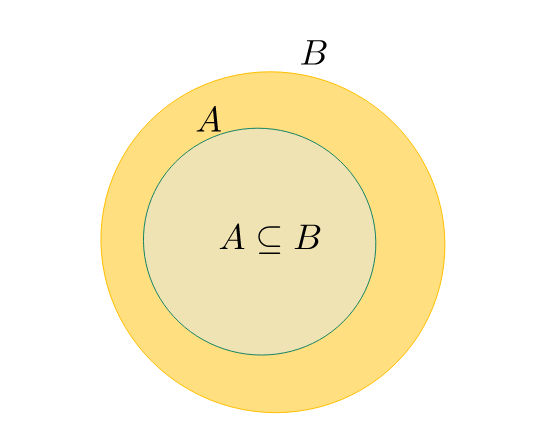
Sottoinsieme proprio: $A \subset B$ o $B \supset A$

$$A \subset B \quad \iff \quad \forall x \in A \colon x \in B \quad \text{ e } \quad \exists y \in B \colon y \not\in A$$

Uguaglianza: $A = B$

$$A = B \quad \iff \quad A \subseteq B \;\land\; B \subseteq A$$

Insieme delle parti

Insieme delle parti $\mathcal{P}(A)$: l'insieme formato da tutti i sottoinsiemi di $A$

Esempio

Se $A={1,\ 2,\ 3}$ allora $$ \mathcal{P}(A)= \big\{\emptyset, {1}, {2}, {3}, {1,2}, {1,3}, {2,3}, {1,2,3}\big\} $$

In totale $2^{|A|}=2^3=8$ elementi

Operazioni con gli insiemi

Unione

$A \cup B = {x \colon x \in A \;\lor\; x \in B}$

Nota:

• Gli elementi di A e quelli di B
• $A\cup\emptyset = A$

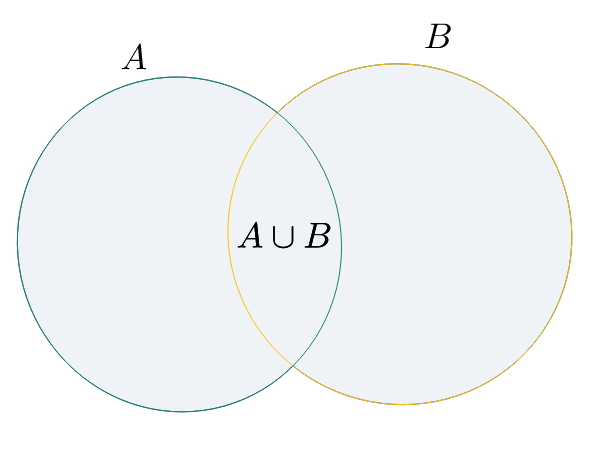
Esempio

Se $$A = {0,\ 1,\ 2}\quad\text{ e }\quad B = {1,\ 2,\ 3}$$ allora $$A \cup B = {0,\ 1,\ 2,\ 3}$$

Intersezione

$A \cap B = {x \colon x \in A \;\land\; x \in B}$

Nota:

• Gli elementi comuni di A e B
• $A\cap\emptyset = \emptyset$

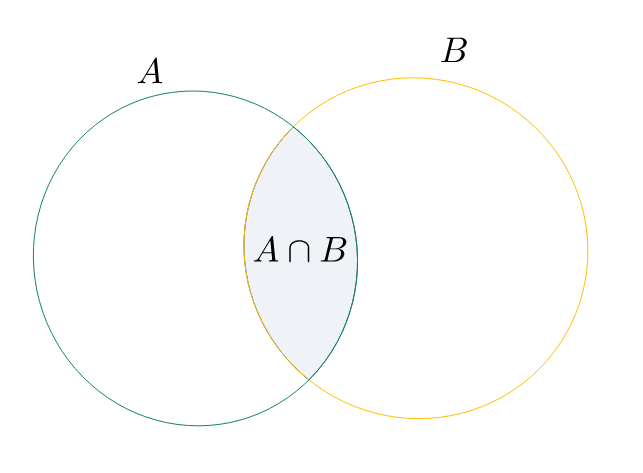
Esempio

Se $$A = {0,\ 1,\ 2}\quad\text{ e }\quad B = {1,\ 2,\ 3}$$ allora $$A \cap B = {\ 1,\ 2}$$

Differenza

$A \setminus B = {x \colon x \in A \;\land\; x \not\in B}$

Nota:

• Gli elementi di A che non sono elementi di B
• $A\setminus B \not= B\setminus A$

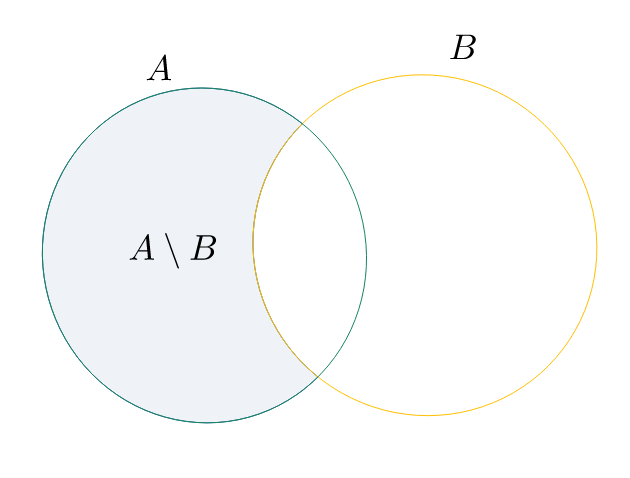
Esempio

Se $$A = {0,\ 1,\ 2}\quad\text{ e }\quad B = {1,\ 2,\ 3}$$ allora $$A \setminus B = {0}$$

Differenza simmetrica

$A\ \Delta\ B = (A\setminus B) \;\cup\; (B\setminus A)$

Nota:

• Gli elementi di A che non sono elementi di B unito gli elementi di $B$ che non sono di $A$

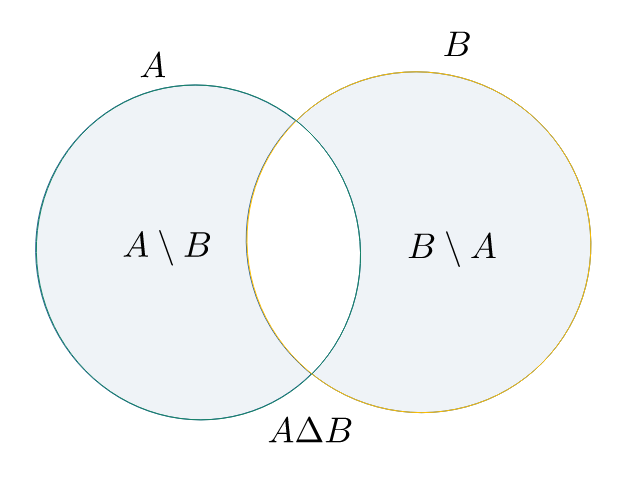
Esempio

Se $$A = {0,\ 1,\ 2}\quad\text{ e }\quad B = {1,\ 2,\ 3}$$ allora $$A\ \Delta\ B = {0,\ 3}$$

Insieme complementare (complementazione)

Se $A\subseteq\mathcal{U}$ allora $A^{c} = \mathcal{U} \setminus A ={x \colon x \in \mathcal{U} \;\land\; x \not\in A}$

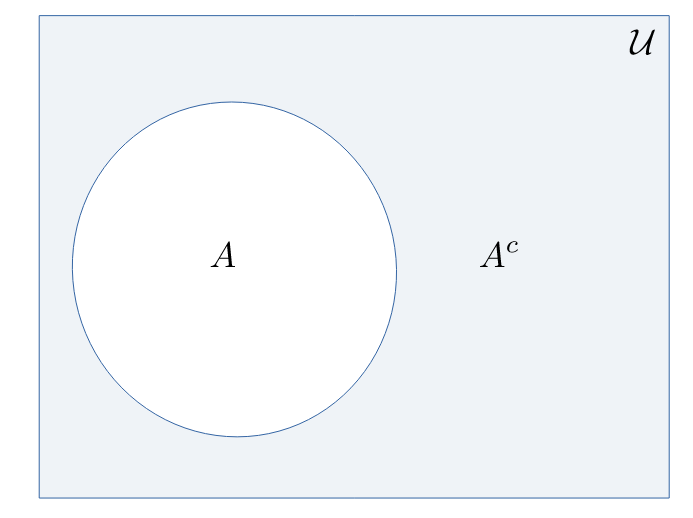
Esempio

Se $$A = {x \in \mathbb{N} \colon x \leqslant 8 }$$ e $$U = {x \in \mathbb{N} \colon x \leqslant 10 }$$ allora $$A^{c} = {9,\ 10}$$

Proprietà

Unione

• Idempotenza: $A \cup A = A$
• Commutativa: $A \cup B = B \cup A$
• Associativa: $(A \cup B) \cup C = A \cup (B \cup C)$
• Distributiva: $A \cup (B \cap C) = (A \cup B) \cap (A \cup C)$
• Di assorbimento: $A \cup (A \cap B) = A$
• Di inclusione: $A \subseteq B \iff (A\cup B = B)$

Intersezione

• Idempotenza: $A \cap A = A$
• Commutativa: $A \cap B = B \cap A$
• Associativa: $(A \cap B) \cap C = A \cap (B \cap C)$
• Distributiva: $A \cap (B \cup C) = (A \cap B) \cup (A \cap C)$
• Di assorbimento: $A \cap (A \cup B) = A$
• Di inclusione: $A \subseteq B \iff (A\cap B = A)$

Complementarietà

• De Morgan unione: $(A \cup B)^{c} = A^{c} \cap B^{c}$
• De Morgan intersezione: $(A \cap B)^{c} = A^{c} \cup B^{c}$
• Involutoria: $(A^{c})^{c} = A$
• Leggi complementari:
  • $A \cup A^{c} = \mathcal{U}$
  • $A \cap A^{c} = \emptyset$
  • $\emptyset^{c}= \mathcal{U}$
  • $\mathcal{U}^{c} = \emptyset$
  • Se $A\subseteq B$ allora $B^{c}\subseteq A^{c}$

Curiosità

• I diagrammi di Venn (1834–1923) furono introdotti per spiegare in modo elementare la teoria degli insiemi e della probabilità

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).