Esercizi parte 3 sui numeri complessi 4/4
Indice degli esercizi (corso Analisi Matematica 1)
Risolvere le equazioni (con rappresentazione grafica delle soluzioni)
- $\quad \left(\operatorname{Re}(z)+2\right)^3 \left(|z+(1+i)|-6\right)^2=0$
- $\quad z^4-(2-i)z^2+1-i=0$
- $\quad |z-1|^2 + z^2 + z - 2=0$
Risolere le disequazioni
- $\quad 2|z|^2 \leqslant (z^2+\bar{z}^2)+|z+\bar{z}|+2$
- $\quad \left(|z+i|-4\right) \cdot \left({|z|\over |z-2|}-1\right) \leqslant 0$
Soluzione
Esercizio 1
Risolvere l'equazione $\left(\operatorname{Re}(z)+2\right)^3 \left(|z+(1+i)|-6\right)^2=0$
Soluzione
Per la legge dell'annullamento del prodotto si ha
$$ \left(\operatorname{Re}(z)+2\right)^3 \left(|z+(1+i)|-6\right)^2=0\\ \quad\iff\quad\\ \left\{ \left(\operatorname{Re}(z)+2\right)^3 = 0 \quad\lor\quad \left(|z+(1+i)|-6\right)^2=0 \right\} $$
Soluzione: $\left(\operatorname{Re}(z)+2\right)^2 = 0$
Si ha
$$ \left(\operatorname{Re}(z)+2\right)^3 = 0 \quad\iff\quad \operatorname{Re}(z)+2 = 0 $$
Posto $z=x+iy$ si ha
$$ \operatorname{Re}(z)+2 = 0 \quad\iff\quad x+2 = 0 \quad\iff\quad x=-2 $$
Si tratta di una retta verticale di equazione $x=-2$
Soluzione: $\left(|z+(1+i)|-6\right)^2=0$
Si ha
$$ \left(|z+(1+i)|-6\right)^2=0 \quad\iff\quad |z+(1+i)|-6=0 $$
Ora, si ha
$$ |z+(1+i)|-6=0 \quad\iff\quad |z+(1+i)|=6 $$
Si tratta di una circonferenza centrata in $z_0=-(1+i)$ e raggio $6$
Soluzione finale
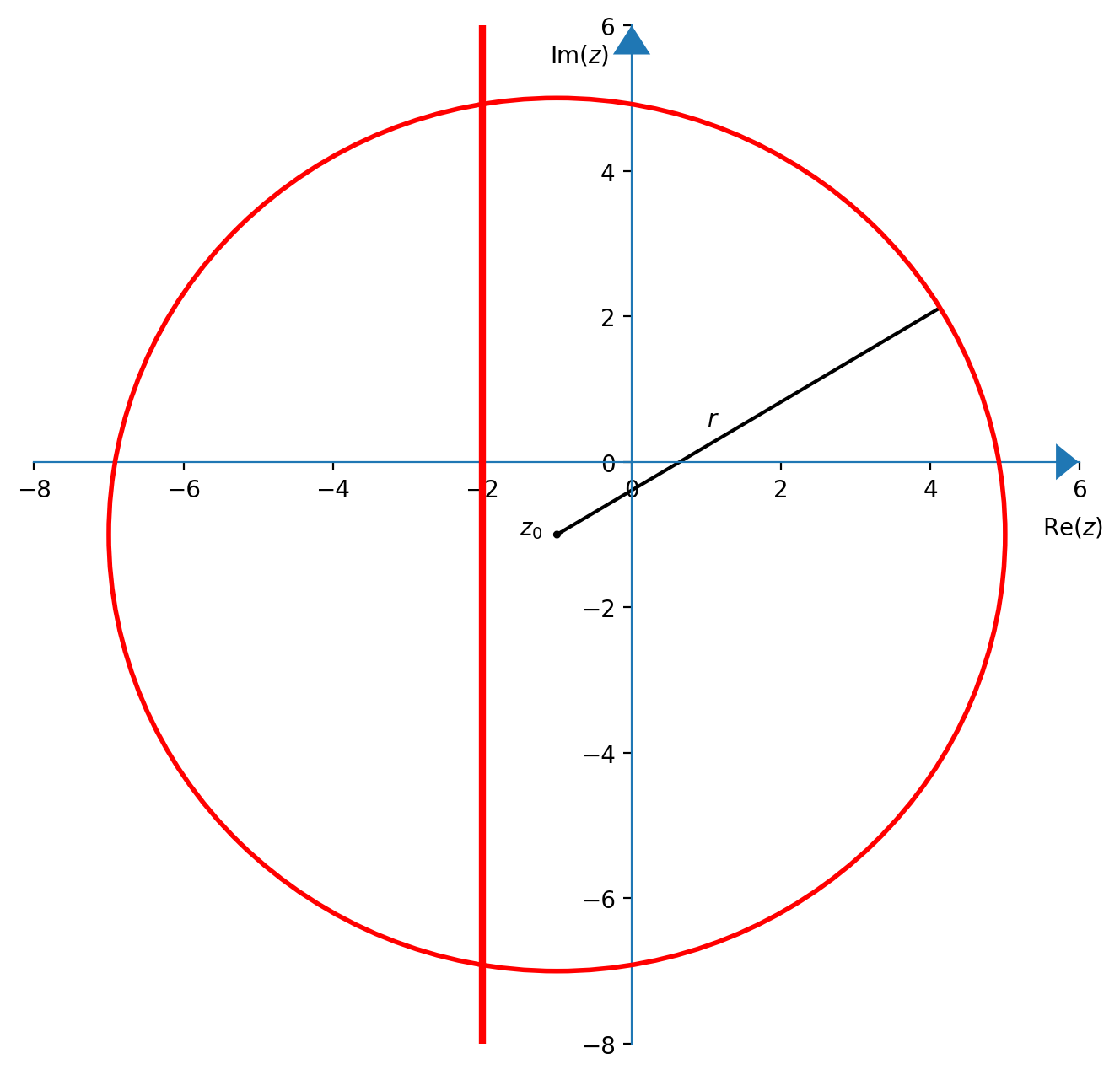
- $x=-2$ (retta verticale)
- $|z+(1+i)|=6$ (circonferenza centrata in $z_0=-(1+i)$ e raggio $6$)
Esercizio 2
Risolvere l'equazione $z^4-(2-i)z^2+1-i=0$
Soluzione
Si tratta di una equazione biquadratica la cui soluzione è
$$\begin{aligned} z^2 &=\; {(2-i) + \sqrt{(2-i)^2-4(1-i)}\over 2} \;=\; {(2-i) + \sqrt{\cancel{4}-1-\cancel{4i}-\cancel{4}+\cancel{4i}}\over 2} \\ &=\; {(2-i) + \sqrt{-1}\over 2} \;=\; {(2-i) \pm i \over 2} \;=\; \begin{cases}1\\1-i\end{cases} \end{aligned}$$
Ora
$$z^2=1 \;\implies\;z_{1,2} = \pm1$$
Calcoliamo
$$z^2=1-i \;\implies\; z_{3,4} = \sqrt{1-i}$$
Dato $\Delta = 1-i$ si ha
- $|\Delta| = \sqrt{2}$, e $\Delta\in\text{IV quadrante}$
- $\theta \;=\; \arg{\Delta} \;=\; \arctan{\left({-1\over1}\right)} \;=\; -{\pi\over4}$
- Forma trigonometrica: $\Delta \;=\; \sqrt{2}\operatorname{cis}{\left(-{\pi\over4}\right)}$
Le radici di $\Delta$ sono
- $\Delta_{0} \;=\; \sqrt{\sqrt{2}} \cdot \operatorname{cis}{\left(-{\pi\over8}\right)} \;=\;\sqrt[4]{2}\cdot \operatorname{cis}{\left(-{\pi\over8}\right)}$
- $\Delta_{1} \;=\; - \Delta_0$
Serve valutare $\sin$ e $\cos$ in $-{\pi\over8}$ a partire dalla valutazioni in $-{\pi\over4}$
Da $\Delta = 1-i$ si ha
- $-{\pi\over2} < \theta < 0$ (permette di scegliere correttamente il segno)
- $\cos{\theta} \;=\; {\sqrt{2}\over2}$
- $\sin{\theta} \;=\; -{\sqrt{2}\over2}$
Dalle formula di bisezione si ha
- $-{\pi\over2} < \theta < 0 \quad\implies\quad -{\pi\over4} < \theta < 0$ ($\cos$ positivo e $\sin$ negativo)
- $\cos{\left(-{\pi\over8}\right)} \;=\; \sqrt{{1+{\sqrt{2}\over2}\over2}} \;=\; {1\over2}\sqrt{2+\sqrt{2}}$
- $\sin{\left(-{\pi\over8}\right)} \;=\; -\sqrt{{1-{\sqrt{2}\over2}\over2}} \;=\; -{1\over2}\sqrt{2-\sqrt{2}}$
Da
$$\Delta_{0} \;=\; \sqrt[4]{2}\cdot \operatorname{cis}{\left(-{\pi\over8}\right)}$$
e
- $\cos{\left(-{\pi\over8}\right)} \;=\; {1\over2}\sqrt{2+\sqrt{2}}$
- $\sin{\left(-{\pi\over8}\right)} \;=\; -{1\over2}\sqrt{2-\sqrt{2}}$
si ha
$$\begin{aligned} z_3 &=\; \Delta_{0} \;=\; {\sqrt[4]{2}\over 2} \left( \sqrt{2+\sqrt{2}} - i \sqrt{2-\sqrt{2}} \right)\\ z_4 &=\; -\Delta_{0} \;=\; -z_3 \end{aligned}$$
Esercizio 3
Risolvere l'equazione $|z-1|^2 + z^2 + z - 2=0$
Soluzione
Posto $z=x+iy$ si ha
$$\begin{gathered} |x-1+iy|^2 + (x+iy)^2 + (x+iy) - 2=0\\ \iff\\ (x-1)^2+\cancel{y^2} + x^2-\cancel{y^2}+i2xy +x+iy - 2 = 0\\ \iff\\ x^2-2x+1 + x^2 +i2xy +x+iy - 2 = 0\\ \iff\\ (2x^2-x-1) + i(2xy+y) = 0 \end{gathered}$$
L'equazione
$$ (2x^2-x-1) + i(2xy+y) = 0 $$
corrisponde al sistema di equazioni
$$ \begin{cases} 2x^2-x-1 = 0\\ 2xy+y = 0 \end{cases} \quad\iff\quad \begin{cases} 2x^2-x-1 = 0\\ y(2x+1) = 0 \end{cases} $$
Dalla seconda si ricava
$$ \left\{y=0\right\}\quad\lor\quad \left\{x=-{1\over2}\right\} $$
Primo caso
Per
$$ y=0 $$
si ha
$$ \begin{cases} 2x^2-x-1 = 0\\ y=0 \end{cases} \quad\iff\quad x_{1,2} = {1\pm\sqrt{1+8}\over 4} = \left\{1,\ -{1\over 2}\right\} $$
quindi le soluzioni sono
- $z_1 = (1,0) = 1$
- $z_2 = \left(-{1\over 2},0\right) = -{1\over 2}$
Secondo caso
Per
$$ x=-{1\over2} $$
si ha
$$ \begin{cases} 2x^2-x-1 = 0\\ x=-{1\over2} \end{cases} \quad\iff\quad \begin{cases} 0 = 0\\ x=-{1\over2} \end{cases} $$
quindi la prima equazione è soddisfatta per ogni $y$, i.e. le soluzioni sono della forma $z = -{1\over2} + iy$
Per rappresentare graficamente le soluzioni abbiamo
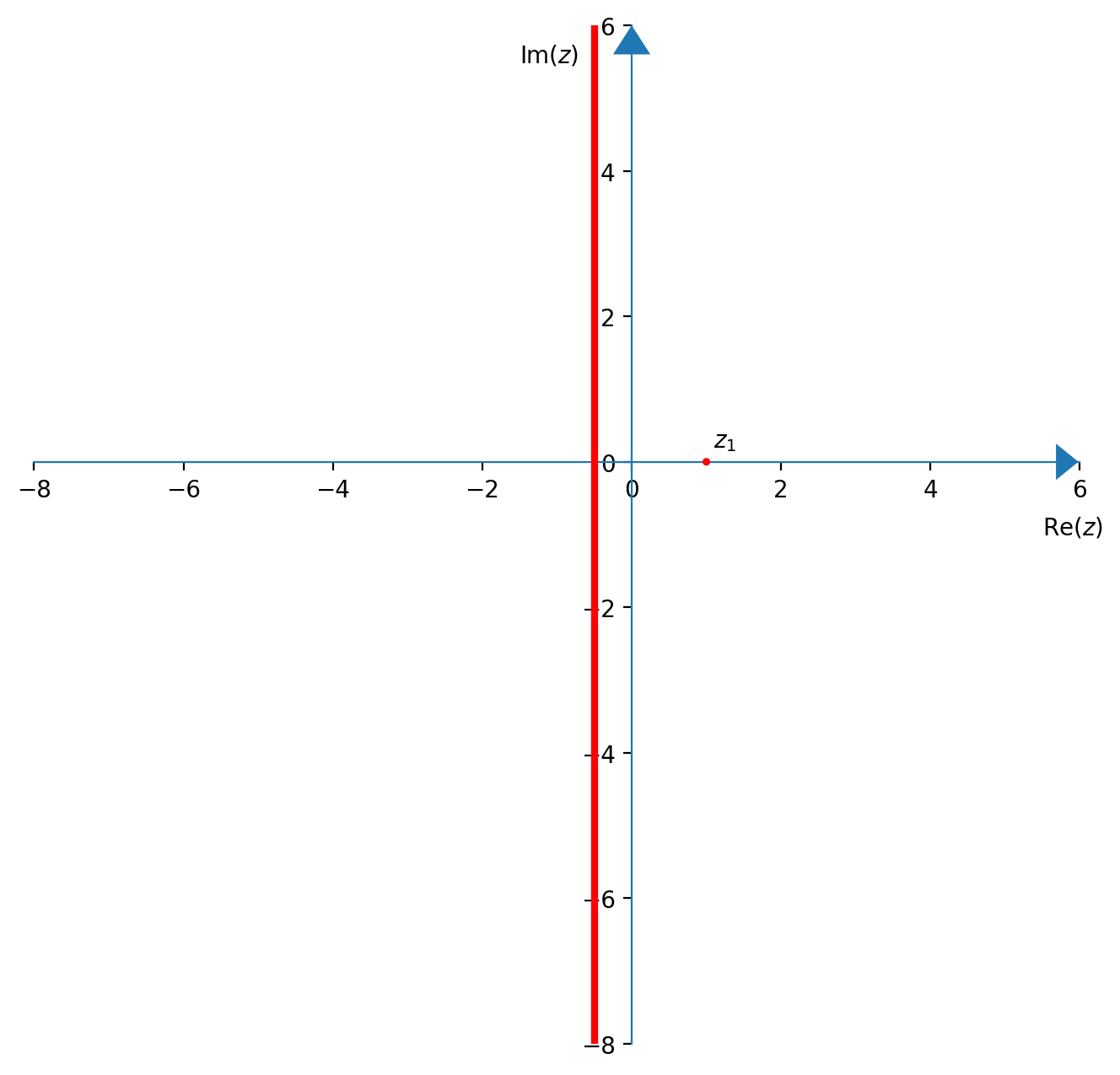
- $z_1 = (1,0) = 1$
- $z_2 = \left(-{1\over 2},0\right) = -{1\over 2}$
- $z = -{1\over2} + iy$ (per ogni $y$)
Esercizio 4
Risolvere la disequazione $2|z|^2 \leqslant (z^2+\bar{z}^2)+|z+\bar{z}|+2$
Soluzione
Posto $z= x+iy$ si ha
$$\begin{gathered} 2(x^2+y^2) \leqslant (x^2-y^2+\cancel{2ixy} + x^2-y^2-\cancel{2ixy}) + |x+\cancel{iy} + x-\cancel{iy}| +2\\ \iff\\ \cancel{2x^2}+2y^2 \leqslant \cancel{2x^2}-2y^2 + 2|x| + 2\\ \iff\\ 4y^2 \leqslant 2|x| + 2\\ \iff\\ 2y^2 \leqslant |x| + 1\\ \end{gathered}$$
Ricordando la definizione di valore assoluto $|x|>a \;\iff\; \left\{x\leqslant-a\right\} \;\lor\; \left\{x\geqslant a\right\}$ si ha
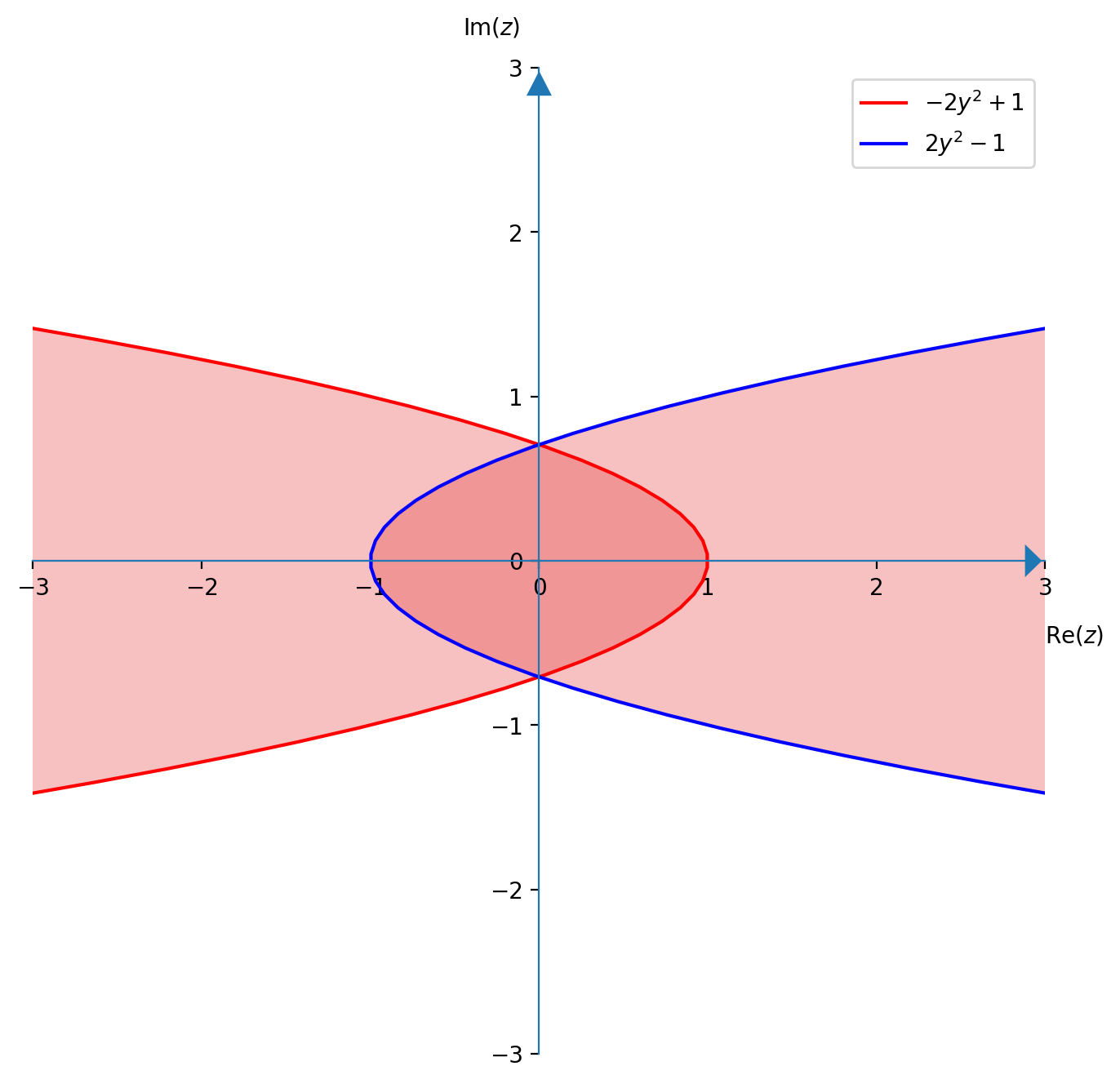
$$\begin{gathered} 2y^2 \leqslant |x| + 1 \quad\iff\quad |x| \geqslant 2y^2 - 1 \\ \iff\\ \left\{x \leqslant -2y^2 +1\right\} \quad\lor\quad \left\{x \geqslant 2y^2 - 1\right\} \end{gathered}$$
La soluzione è rappresentata in figura
Esercizio 5
Risolvere la disequazione $\left(|z+i|-4\right) \cdot \left({|z|\over |z-2|}-1\right) \leqslant 0$
Soluzione
Dobbiamo imporre la condizione di esistenza per il secondo fattore: $z\ne2$
Applichiamo lo studio del segno
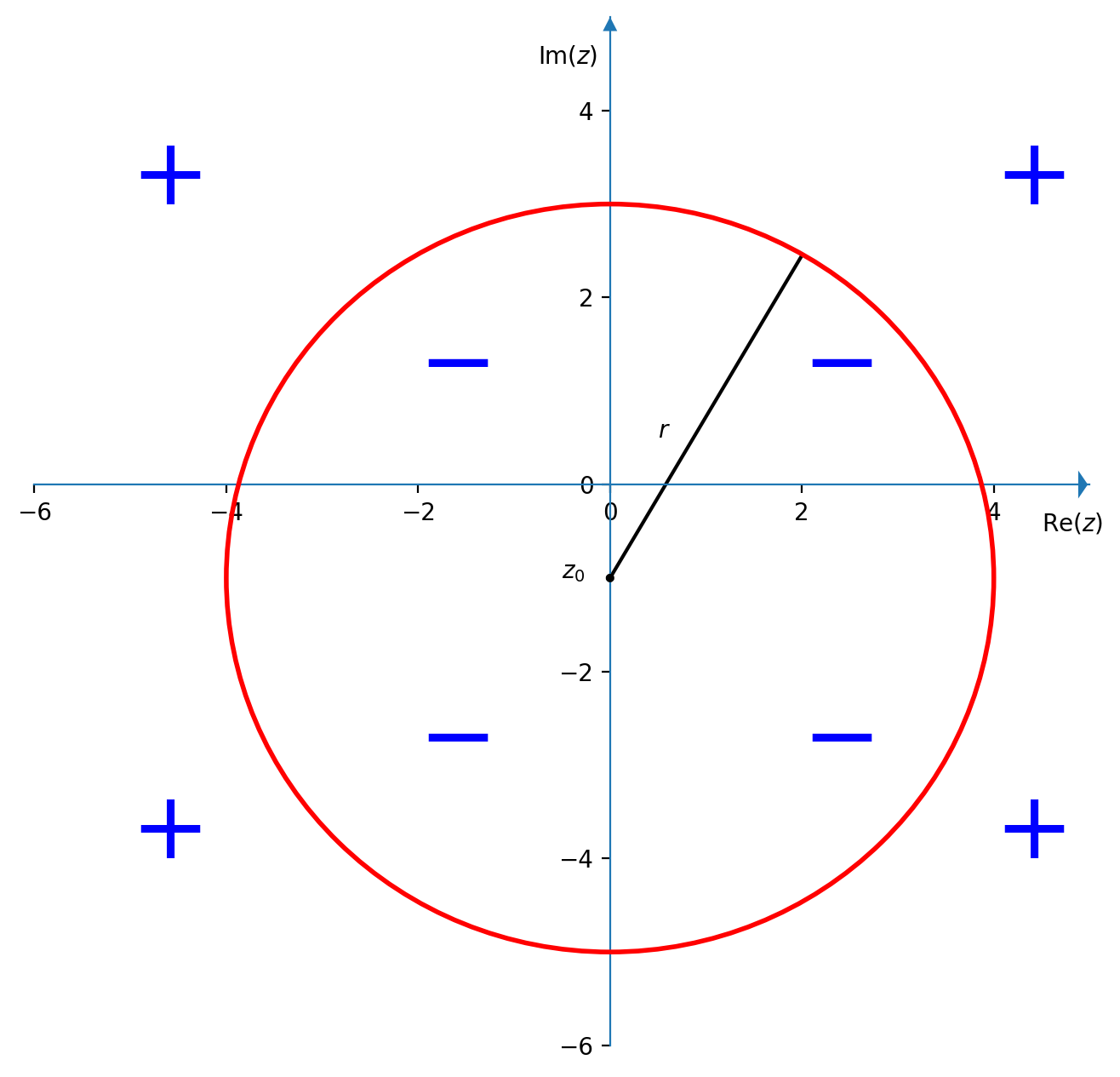
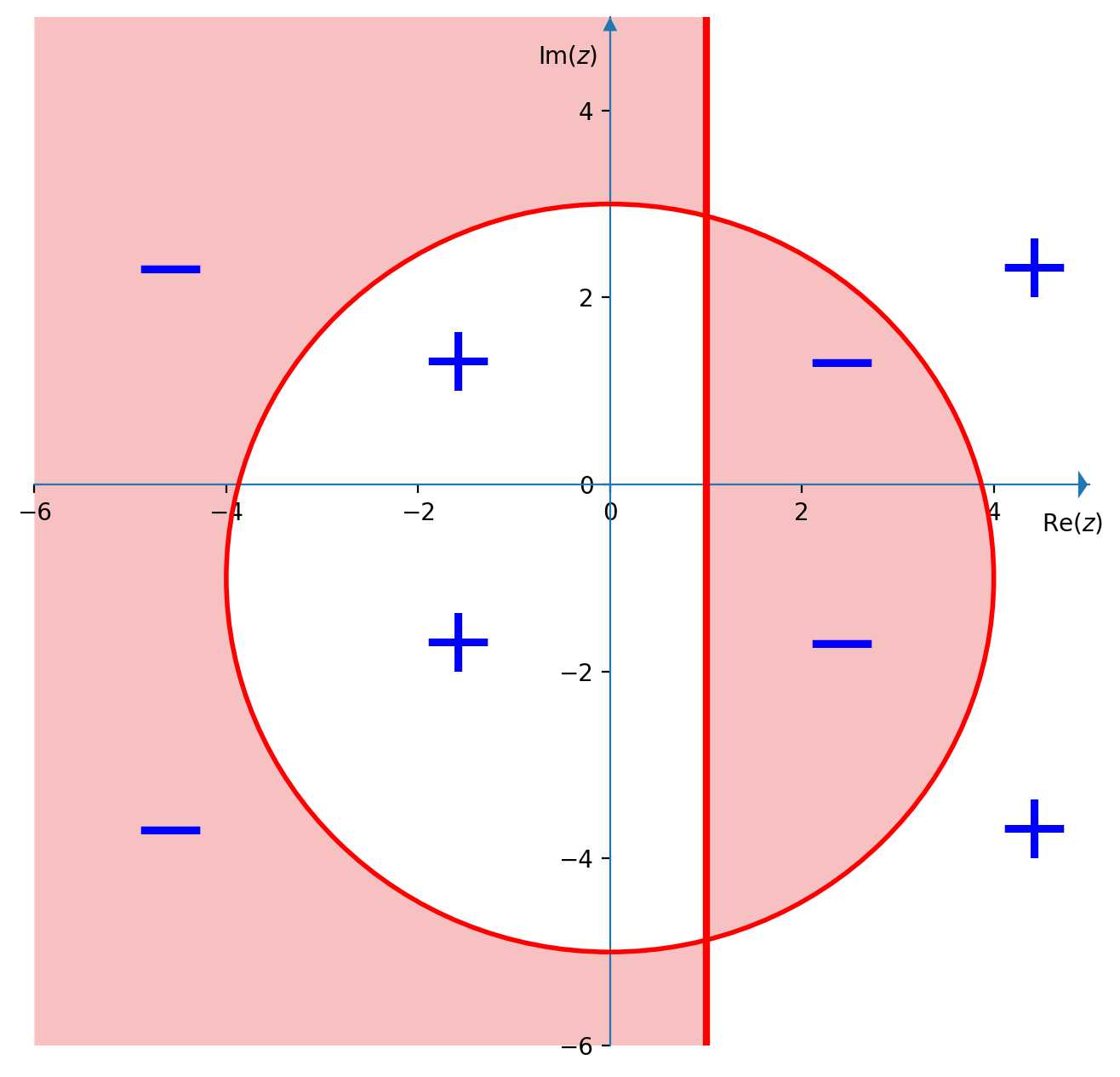
- $\left(|z+i|-4\right)\geqslant 0 \;\iff\; |z-(-i)| \geqslant 4$ rappresenta un cerchio centrato in $z_0=-i$ e raggio $r=4$; è negativo per valori interni alla circonferenza e positivo per valori esterni
Studiamo il segno di ${|z|\over |z-2|}-1$
:::::::::::::: {.columns align=top .onlytextwidth} :::: {.column width=50%}
Posto $z=x+iy$ si ha
$$\begin{gathered} {|z|\over |z-2|}-1 \geqslant 0 \quad\iff\quad {|z|\over |z-2|} \geqslant 1 \\ \iff \text{(il modulo è sempre positivo)}\\ |z| \geqslant |z-2| \\ \iff\\ x^2 + y^2 \geqslant (x-2)^2 + y^2 \\ \iff\\ 0 \geqslant -4x + 4 \\ \iff\\ x \geqslant 1 \end{gathered}$$
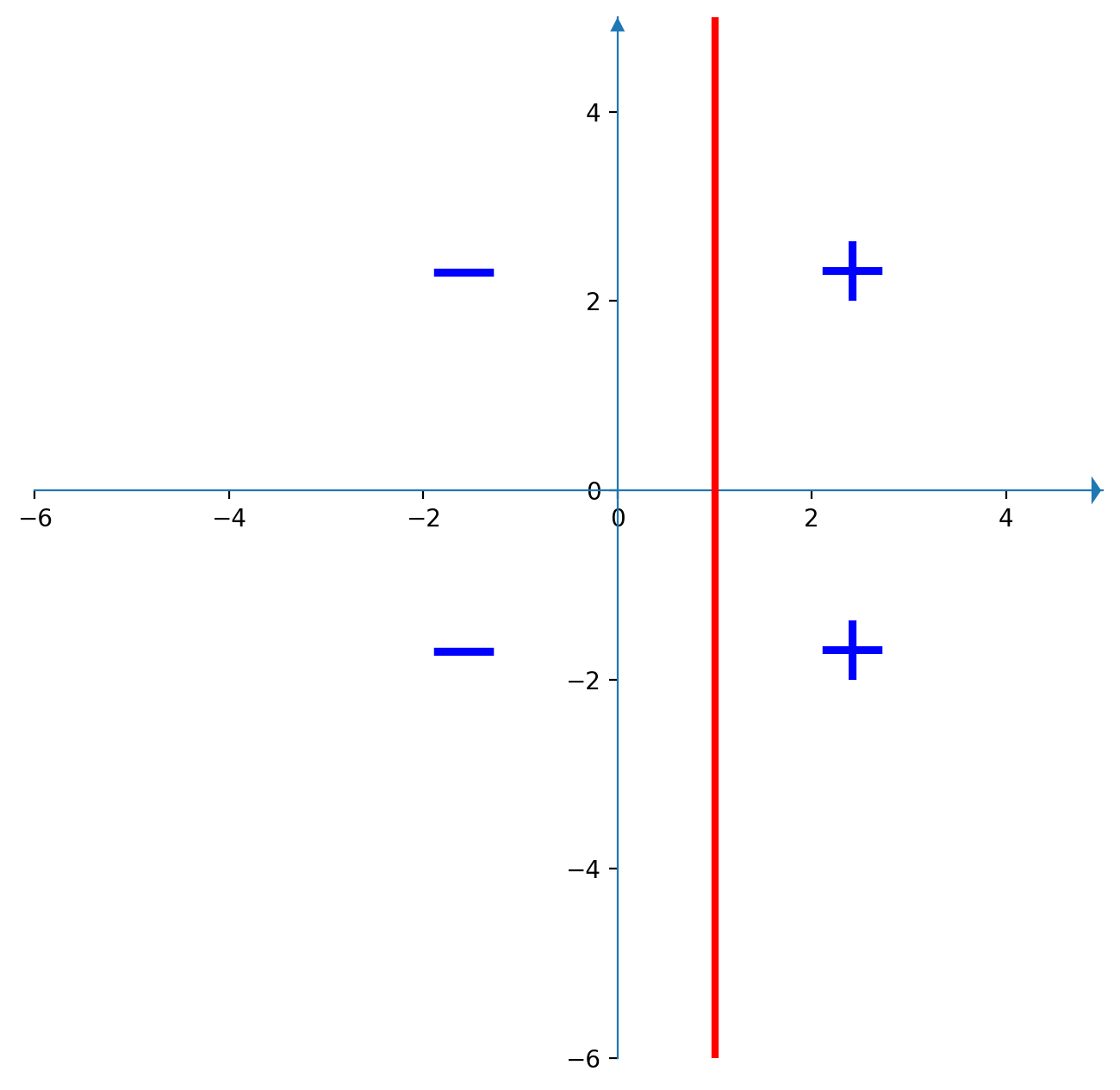
Soluzione finale
Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).
