Esercizi parte 3 sui numeri complessi 3/4

Indice degli esercizi (corso Analisi Matematica 1)

Risolvere le equazioni

$\quad\left|z+2i\right|\;=\;\left|\left|z\right|-2\right|$
$\quad z\left|z\right|\;=\;2\overline{z}$
$\quad2z^2+\sqrt{2}(1-i)z+1\;=\;0$ con soluzioni in forma algebrica

Risolere le disequazioni

$\quad\left|\overline{z}-a\right| \leqslant \left|\operatorname{Re}{\left(z+a\right)}\right|$ con $a\in\mathbb{R}$ e $a>0$
$\quad\left|\arg{z}\right| < {\pi\over 3}$

VIDEO

PDF

Soluzione

Esercizio 1

Risolvere l'equazione

$$\left|z+2i\right|\;=\;\left|\left|z\right|-2\right|$$

Soluzione

Posto $z=x+iy$ si ha $$ \begin{gathered} \left|x+iy+2i\right| \;=\; \left|\sqrt{x^2+y^2}-2\right| \\ \sqrt{x^2+y^2+4y+4} \;=\; \left|\sqrt{x^2+y^2}-2\right| \\ x^2+y^2+4y+4 \;=\; x^2+y^2+4 -4\sqrt{x^2+y^2}\\ 4y \;=\; -4\sqrt{x^2+y^2} \quad\implies\quad -y \;=\; \sqrt{x^2+y^2} \end{gathered} $$

Elevando al quadrato $$-y = \sqrt{x^2+y^2} \;\text{ con }\; y\leqslant 0$$ si ha $$ y^2 = x^2 + y^2 \;\implies\; x^2=0 \;\implies\; x=0 $$

Quindi le soluzioni sono della forma $z=0+iy$ con $y\leqslant0$

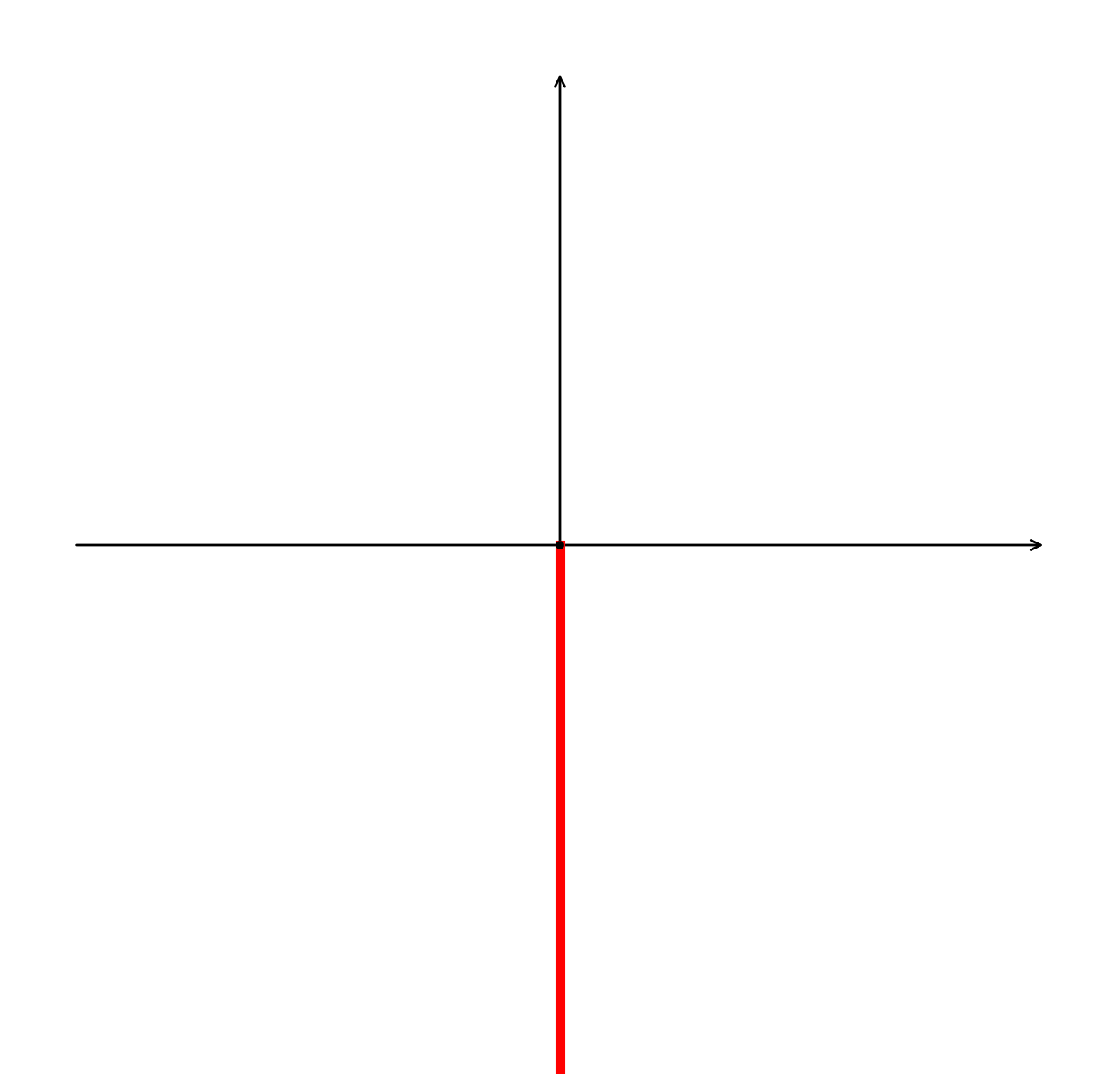
Esercizio 2

Risolvere l'equazione $$z\left|z\right|\;=\;2\overline{z}$$

Soluzione

Due strategie:

forma algebrica
forma esponenziale

Soluzione (metodo 1)

In forma algebrica si ha

$$ (x+iy)\sqrt{x^2+y^2} = 2(x-iy) $$

Uguagliando parte reale e immaginaria si hanno le equazioni $$ \begin{cases} x\sqrt{x^2+y^2} = 2x\\ y\sqrt{x^2+y^2} = -2y \end{cases} $$

Se $x\ne0$ si ha

$$ \begin{cases} x\sqrt{x^2+y^2} = 2x\\ y\sqrt{x^2+y^2} = -2y \end{cases} \;\implies\; \begin{cases} \sqrt{x^2+y^2} = 2\\ y \cdot 2 = -2y \end{cases} \;\implies\; \begin{cases} \sqrt{x^2+y^2} = 2\\ y=0 \end{cases}\\ \;\implies\; \begin{cases} |x| = 2\\ y=0 \end{cases} \;\implies\; \begin{cases} x=\pm2\\ y=0 \end{cases} $$

Quindi le soluzioni sono

$$ z= 2 +i0= 2 \quad,\quad z= -2 +i0=-2 $$

Se $x=0$ si ha

allora (dalla seconda) si ha $y|y|=-2y$ i.e. $y=0$ ($|y|=-2$ non ha soluzione)

Quindi le soluzioni sono $$ z=0\quad,\quad z= 2 +i0= 2 \quad,\quad z= -2 +i0=-2 $$

Soluzione (metodo 2)

Utilizzando la forma esponenziale $z=r e^{\left(i\theta\right)}$ l'eq. diventa $$ z\left|z\right|=2\overline{z} \;\implies\; r e^{\left(i\theta\right)}\cdot r = 2 r e^{\left(-i\theta\right)} \;\implies\; r^2 e^{\left(i\theta\right)} = 2 r e^{\left(-i\theta\right)} $$

Ricordando la periodicità dell'esponenziale complesso si ha $$ \begin{cases} r^2 = 2r\\ \theta = -\theta + k 2\pi \end{cases} \;\implies\; \begin{cases} r= {0,2}\\ \theta = k\pi \end{cases} $$ da cui le soluzioni $$ z = \left\{0,\ -2,\ 2\right\} $$

Esercizio 3

Risolvere l'equazione $$2z^2+\sqrt{2}(1-i)z+1\;=\;0$$ esprimendo le soluzioni in forma algebrica

Soluzione

Applicando la formula di secondo grado, le soluzioni sono

$$\begin{aligned} z_{1,2} &= {-\sqrt{2}(1-i) +\sqrt{(\sqrt{2}(1-i))^2-4\cdot 2 \cdot 1} \over 2\cdot2} \;=\; {-\sqrt{2}(1-i) +\sqrt{2(1-i)^2-8} \over 4} \\ &= {-\sqrt{2}(1-i) +\sqrt{2(\cancel{1}-\cancel{1}-2i)-8} \over 4} \;=\; {-\sqrt{2}(1-i) +\sqrt{-4(2+i)}\over 4} \\ &= {-\sqrt{2}(1-i) +2\sqrt{-2-i}\over 4} \end{aligned}$$

Ora, si devono esprimere in forma algebrica!

Dobbiamo calcolare le radici quadrate di $\Delta = -2-i$. Si ha

$|\Delta| = \sqrt{5}$
$\Delta\in\text{III quadrante}$ con $\pi < \theta < {3\over2}\pi$
$\theta \;=\; \arg{\Delta} \;=\; \pi + \arctan{\left({1\over2}\right)}$ (non c'e' soluzione analitica)
Forma trigonometrica: $\Delta \;=\; \sqrt{5}\operatorname{cis}{\left(\theta\right)}$

Le radici di $\Delta$ sono

$\Delta_{0} \;=\; \sqrt{\sqrt{5}} \cdot \operatorname{cis}{\left({\theta\over 2}\right)} \;=\; \sqrt[4]{5} \left(\cos{\left({\theta\over 2}\right)} + i \sin{\left({\theta\over 2}\right)}\right)$
$\Delta_{1} \;=\; - \Delta_0$

Dal risultato

$$\Delta_{0} \;=\;\sqrt[4]{5} \left(\cos{\left({\theta\over 2}\right)} + i \sin{\left({\theta\over 2}\right)}\right)$$

serve solo valutare $\sin$ e $\cos$ in ${\theta\over 2}$

Da $\Delta = -2-i$, si ha

$\pi < \theta < {3\over2}\pi$ (permette di scegliere correttamente il segno)
$\cos{\theta} \;=\; -{2\over\sqrt{5}}$
$\sin{\theta} \;=\; -{1\over\sqrt{5}}$

Dalle formule di bisezione si ha

$\pi < \theta < {3\over2}\pi \quad\implies\quad {\pi\over 2} < {\theta\over 2} < {3\pi\over4}$ ($\cos$ negativo e $\sin$ positivo)
$\cos{\left({\theta\over 2}\right)} \;=\; - \sqrt{{1-{2\over\sqrt{5}}\over 2}} \;=\; - \sqrt{{\sqrt{5}-2\over2\sqrt{5}}}$
$\sin{\left({\theta\over 2}\right)} \;=\; \sqrt{{1+{2\over\sqrt{5}}\over 2}} \;=\; \sqrt{{\sqrt{5}+2\over2\sqrt{5}}}$

$$\Delta_{0} \;=\;\sqrt[4]{5} \left(\cos{\left({\theta\over 2}\right)} + i \sin{\left({\theta\over 2}\right)}\right)$$

$\cos{\left({\theta\over 2}\right)} \;=\; - \sqrt{{\sqrt{5}-2\over2\sqrt{5}}}$
$\sin{\left({\theta\over 2}\right)} \;=\; \sqrt{{\sqrt{5}+2\over2\sqrt{5}}}$

si ha

$$\begin{aligned} \Delta_{0} &=\; \sqrt[4]{5} \left( - \sqrt{{\sqrt{5}-2\over2\sqrt{5}}} + i \sqrt{{\sqrt{5}+2\over2\sqrt{5}}} \right) \;=\; {1\over \sqrt{2}} \left( - \sqrt{\sqrt{5}-2} + i \sqrt{\sqrt{5}+2} \right)\\ \Delta_{1} &=\; -\Delta_{0} \end{aligned}$$

Pertanto le soluzioni sono

$$\begin{aligned} z_{1,2} &=\; {-\sqrt{2}(1-i) +2\sqrt{-2-i}\over 4}\\[1em] &=\; {-\sqrt{2}(1-i) \pm 2\cdot {1\over \sqrt{2}} \left( - \sqrt{\sqrt{5}-2} + i \sqrt{\sqrt{5}+2} \right) \over 4}\\[1em] &=\; \begin{cases} {-\sqrt{2}(1-i) + \sqrt{2} \left( - \sqrt{\sqrt{5}-2} + i \sqrt{\sqrt{5}+2} \right) \over 4} \;=\; {\sqrt{2}\over4}\left( - (1+\sqrt{\sqrt{5}-2}) + i(1+ \sqrt{\sqrt{5}+2}) \right)\\ {-\sqrt{2}(1-i) - \sqrt{2} \left( - \sqrt{\sqrt{5}-2} + i \sqrt{\sqrt{5}+2} \right) \over 4} \;=\; {\sqrt{2}\over4}\left( (-1+\sqrt{\sqrt{5}-2}) + i(1- \sqrt{\sqrt{5}+2}) \right)\\ \end{cases} \end{aligned}$$

Esercizio 4

Risolvere la disequazione $\left|\overline{z}-a\right| \leqslant \left|\operatorname{Re}{\left(z+a\right)}\right|$ con $a\in\mathbb{R}$ e $a>0$

Soluzione

Posto $z=x+iy$ si ha $\left|x-iy-a\right| \leqslant \left|x+a\right|$

Elevando al quadrato (entrambi i termini sono positivi), si ha $$ \begin{gathered} (x-a)^2+y^2 \leqslant (x+a)^2 \\ \cancel{x^2} -2ax +\bcancel{a^2} +y^2 \leqslant \cancel{x^2} +2ax +\bcancel{a^2} \\ y^2 \leqslant 4ax \end{gathered} $$ L'equazione $y^2 = 4ax$ rappresenta una parabola lungo l'asse $x$

La soluzione di $y^2 \leqslant 4ax$ (con $a>0$ per ipotesi) è rappresenta in figura

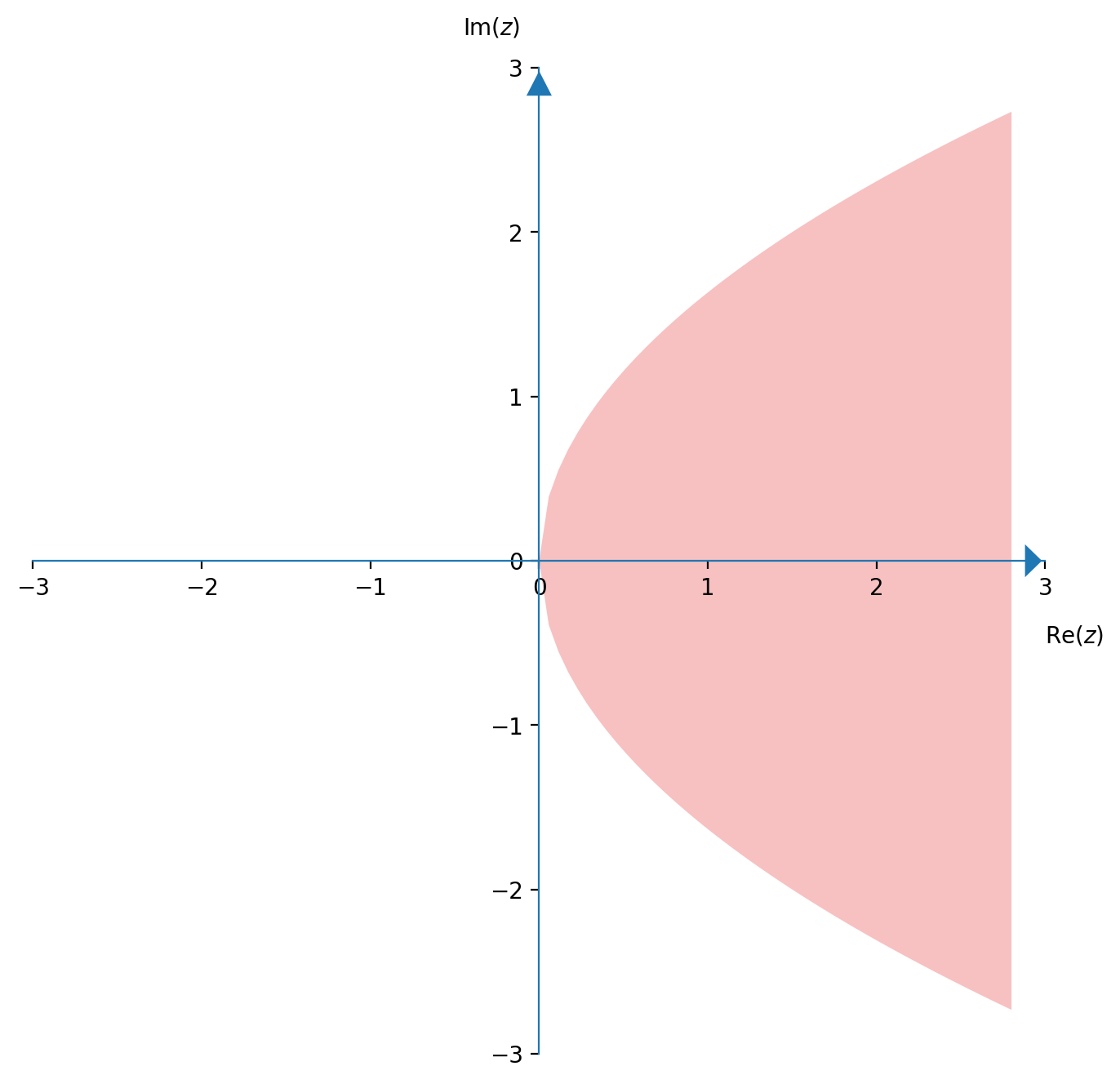
Esercizio 5

Risolvere la disequazione $\left|\arg{z}\right| < {\pi\over 3}$ e rappresentarla graficamente

Soluzione

Se $z=r e^{i\theta}$ allora $\arg{z} = \theta$ e quindi $$ \begin{aligned} &\left|\arg{z}\right| < {\pi\over 3} \\ & \;\Longleftrightarrow\; \left|\theta\right| < {\pi\over 3} \\ & \;\Longleftrightarrow\; \left\{-{\pi\over 3} < \theta < {\pi\over 3}\right\} \end{aligned} $$

L'equazione $z=re^{i\theta_0}$ fissato $\theta_0$ rappresenta una retta passante per l'origine con coefficiente angolare $$ m = \tan{\theta_0} $$

Quindi, la regione $\left|\arg{z}\right| < {\pi\over 3}$ è limitata tra le rette di equazione

$$ \begin{cases} y = \tan{\left({\pi\over 3}\right)}x = \sqrt{3}x \\ y = \tan{\left(-{\pi\over 3}\right)}x = -\sqrt{3}x \\ \end{cases} $$

La soluzione può essere riscritta anche come

$$\begin{cases} \operatorname{Re}(z) >0 \\ -\sqrt{3}\operatorname{Re}(z) < \operatorname{Im}(z) < \sqrt{3}\operatorname{Re}(z) \end{cases}$$

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).