Disequazioni algebriche (complesse)

Obiettivo (corso Analisi Matematica 1)

• Ordinamento e disequazioni
• Disequazioni in campo complesso

Ordinamento e disequazioni

Ordinamento

Ricordiamo che su $\mathbb{C}$ non è possibile definire un ordinamento

Quindi le seguenti scritture non hanno senso $$ \begin{aligned} 1+2i & > -1-2i\\ i &< 2i \end{aligned} $$

Disequazioni

Le disequazioni coinvolgono operazioni da $\mathbb{C}$ a $\mathbb{R}$ e sono del tipo

• Parte reale
• Parte immaginaria
• Modulo e argomento

Per la risoluzione tipicamente si risolvono con la sostituzione algebrica $z=a+bi$ (disequazioni a due incognite) e si rappresentano successivamente le soluzione nel piano di Gauss

Si ricordi che $\left|z-z_0\right| \leqslant r$, con $r>0$, definisce un cerchio di centro $z_0$ e raggio $r$

Esempi

Esempio 1

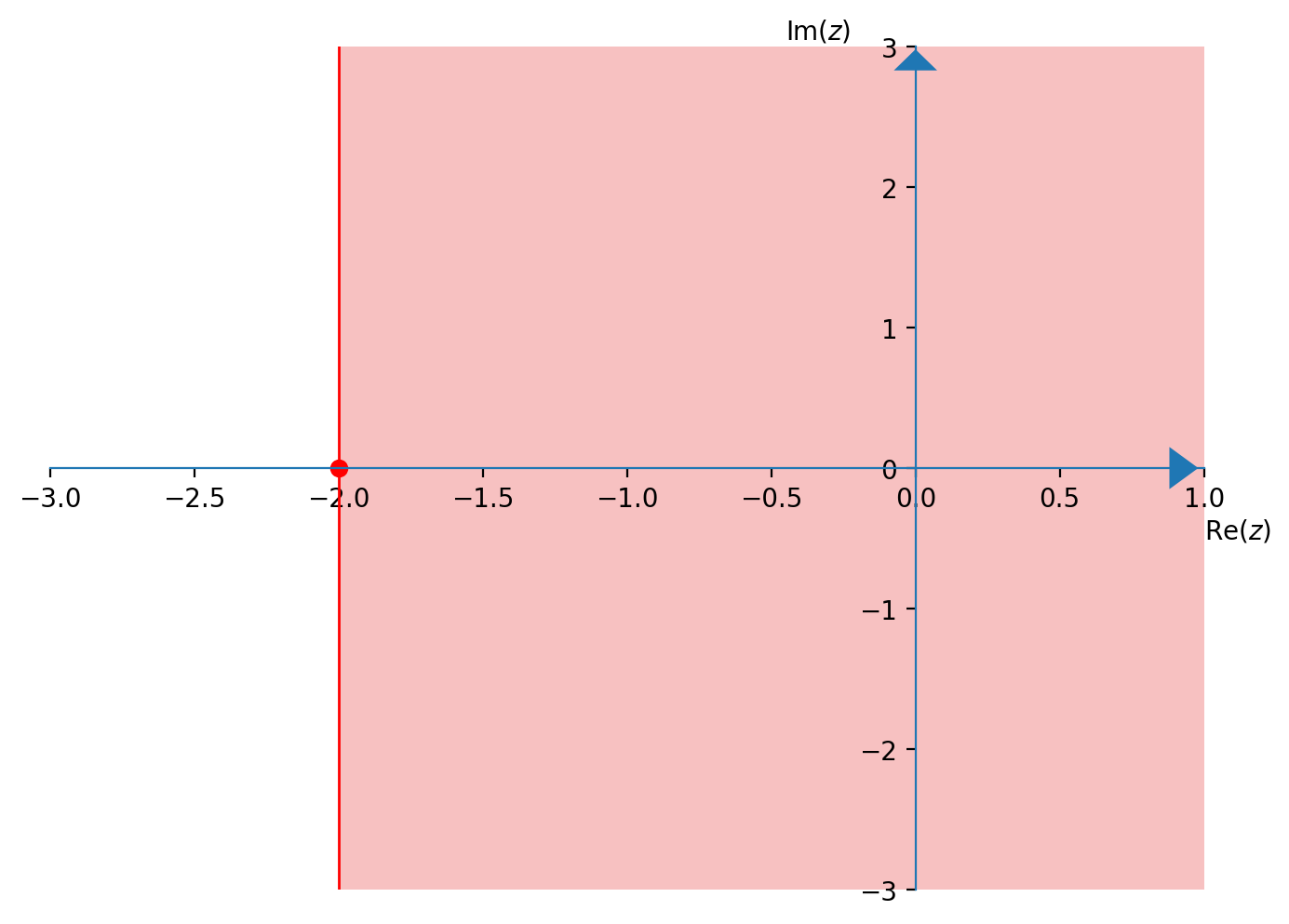
Risolvere la disequazione $\operatorname{Re}(z) \geqslant -2$ e rappresentarla graficamente

Soluzione

Se $z=x+iy$, la disequazione diventa $$ x \geqslant -2 $$ cioè rappresenta il semipiano a destra della retta $$ x=-2 $$

Esempio 2

Risolvere la disequazione $\left|{z-4\over z+2}\right| \geqslant 2$ e rappresentarla graficamente

Soluzione

Se $z=x+iy$ e $z\ne2$, la disequazione diventa $\left|z-4\right| \geqslant 2\left|z+2\right|$ e ha soluzione

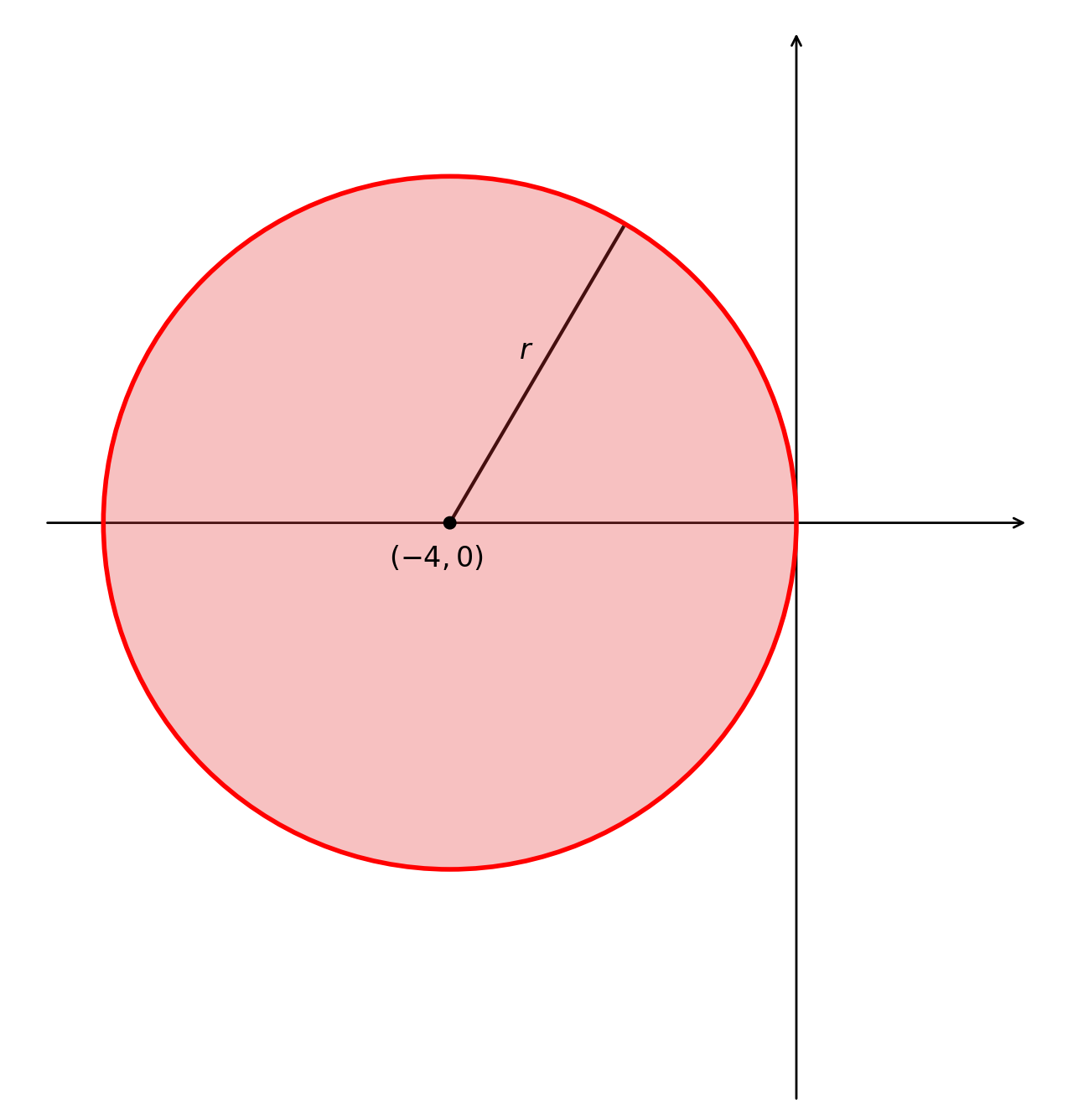
Rappresenta i punti interni ad una circonferenza di centro $(-4,0)$ e raggio 4

Soluzione (alternativa)

Da $\left|z-4\right| \geqslant 2\left|z+2\right|$ elevando al quadrato e ricordano che $\left|z\right|^2 = z \cdot \overline{z}$ si ha $$ \begin{gathered} \left|z-4\right|^2 \geqslant 2^2\left|z+2\right|^2\\ (z-4)\overline{(z-4)} \geqslant 4 (z+2) \overline{(z+2)} \\ (z-4)(\overline{z}-4) \geqslant 4 (z+2) (\overline{z}+2) \\ z \overline{z} -4 z -4 \overline{z} +16 \geqslant 4 \left( z \overline{z} +2 z +2 \overline{z} +4 \right) \\ -3 z \overline{z} - 12 z -12 \overline{z} \geqslant 0 \\ z \overline{z} +4 z +4 \overline{z} \leqslant 0 \\ (z+4)(\overline{z}+4) - 16 \leqslant 0 \\ (z+4)\overline{(z+4)} \leqslant 4^2 \\ \left|z+4\right| \leqslant 4 \end{gathered} $$

Esempio 3

Risolvere la disequazione $$\left||z-2|^2 - |\operatorname{Im}(z)|^2-1\right|\geqslant -\operatorname{Im}(z)+3$$

Soluzione

Posto $z=x+iy$ la disequazione diventa

$$\begin{gathered} \left||z-2|^2 - |\operatorname{Im}(z)|^2-1\right|\geqslant -\operatorname{Im}(z)+3 \\ \left|(x-2)^2 + \cancel{y^2} -\cancel{y^2} -1\right| \geqslant -y+3 \\ y \geqslant 3 - \left|(x-2)^2 -1\right| = 3 - \left|x^2-4x+3\right| \end{gathered}$$

Risolviamo il modulo.

• $x^2-4x+3 = 0 \;\implies\; x_{1,2} = 2 \pm\sqrt{4-3} = 2\pm1 = \left\{1,\ 3\right\}$
• $x^2-4x+3 \geqslant 0 \;\implies\; \left\{x\leqslant 1\right\} \;\lor\; \left\{x\geqslant 3\right\}$

Quindi, la disequazione diventa

$$ y \geqslant 3 - \left|x^2-4x+3\right| \;=\; \begin{cases} -x^2+4x&\text{ se }\left\{x\leqslant 1\right\} \;\lor\; \left\{x\geqslant 3\right\}\\ x^2-4x+6&\text{ se } 1<x<3\\ \end{cases} $$

Definito

$$f(x) = \begin{cases} -x^2+4x&\text{ se }\left\{x\leqslant 1\right\} \;\lor\; \left\{x\geqslant 3\right\}\\ x^2-4x+6&\text{ se } 1<x<3\\ \end{cases} $$

La soluzione è

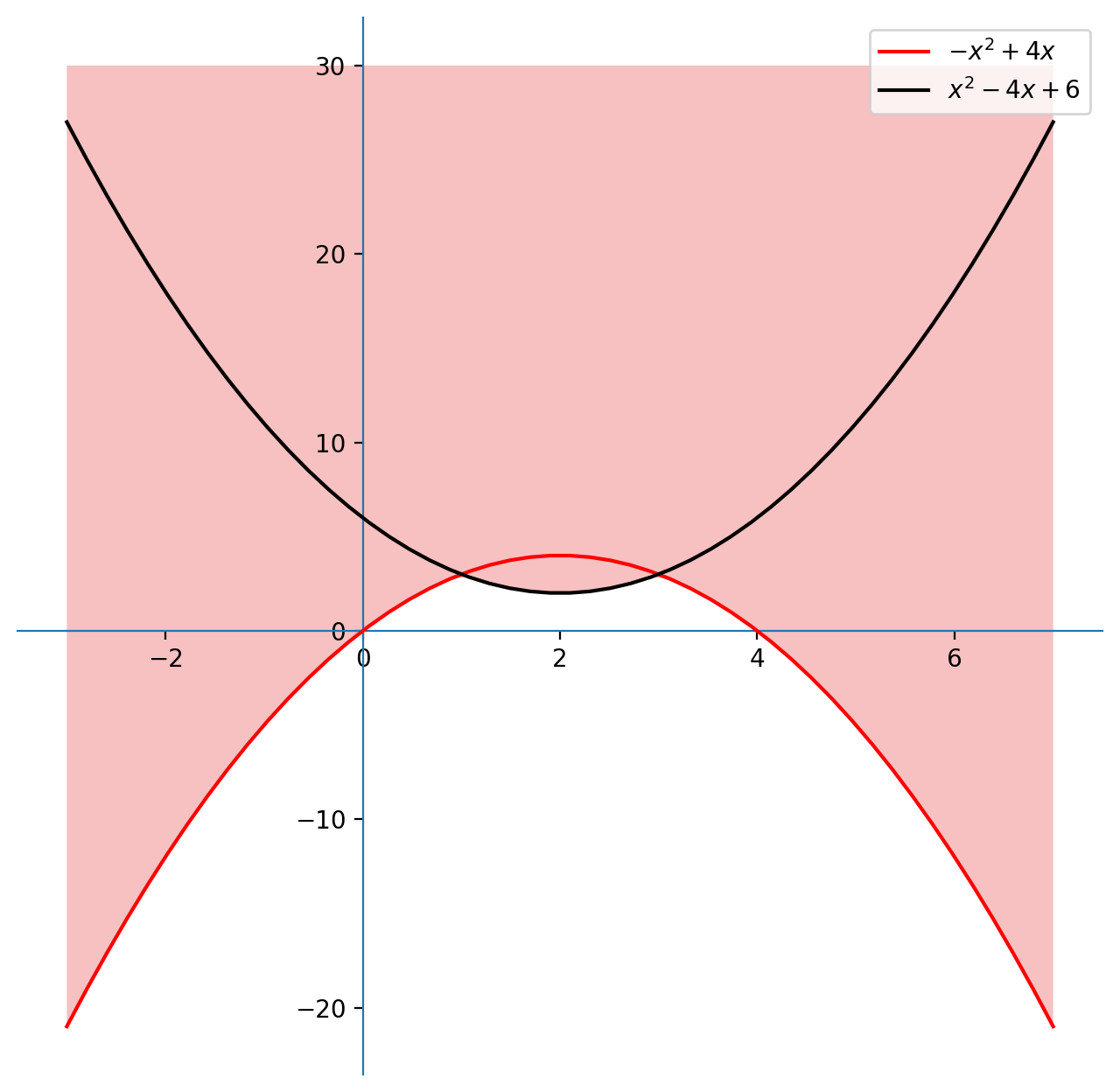
$$ \mathcal{A} = \left\{z=x+iy \in\mathcal{C} \;\colon\; y \geqslant f(x)\right\} $$

Nota: Disegno le due parabole (dalla concavità e dal vertice)

Esempio 4

Risolvere il sistema di disequazioni $$\quad \begin{cases}\operatorname{Re}(z)\geqslant\operatorname{Im}(z)\\ \left|\overline{z}-i\right|\leqslant 2\end{cases}$$

Soluzione

Caso $\operatorname{Re}(z)\geqslant\operatorname{Im}(z)$

Posto $z=x+iy$ si ha $$ \operatorname{Re}(z)\geqslant\operatorname{Im}(z) \;\implies\; y \geqslant x $$ Rappresenta la regione sopra la bisettrice del I-III quadrante

Caso $\left|\overline{z}-i\right|\leqslant2$

Si ha $$ \left|\overline{z}-i\right|\leqslant2 \;\Longleftrightarrow\; \left|\overline{z+i}\right|\leqslant2\;\Longleftrightarrow\; \left|z-(-i)\right|\leqslant2$$ Quindi rappresenta la regione interna ad un cerchio di centro $z_0=-i$ e raggio $2$

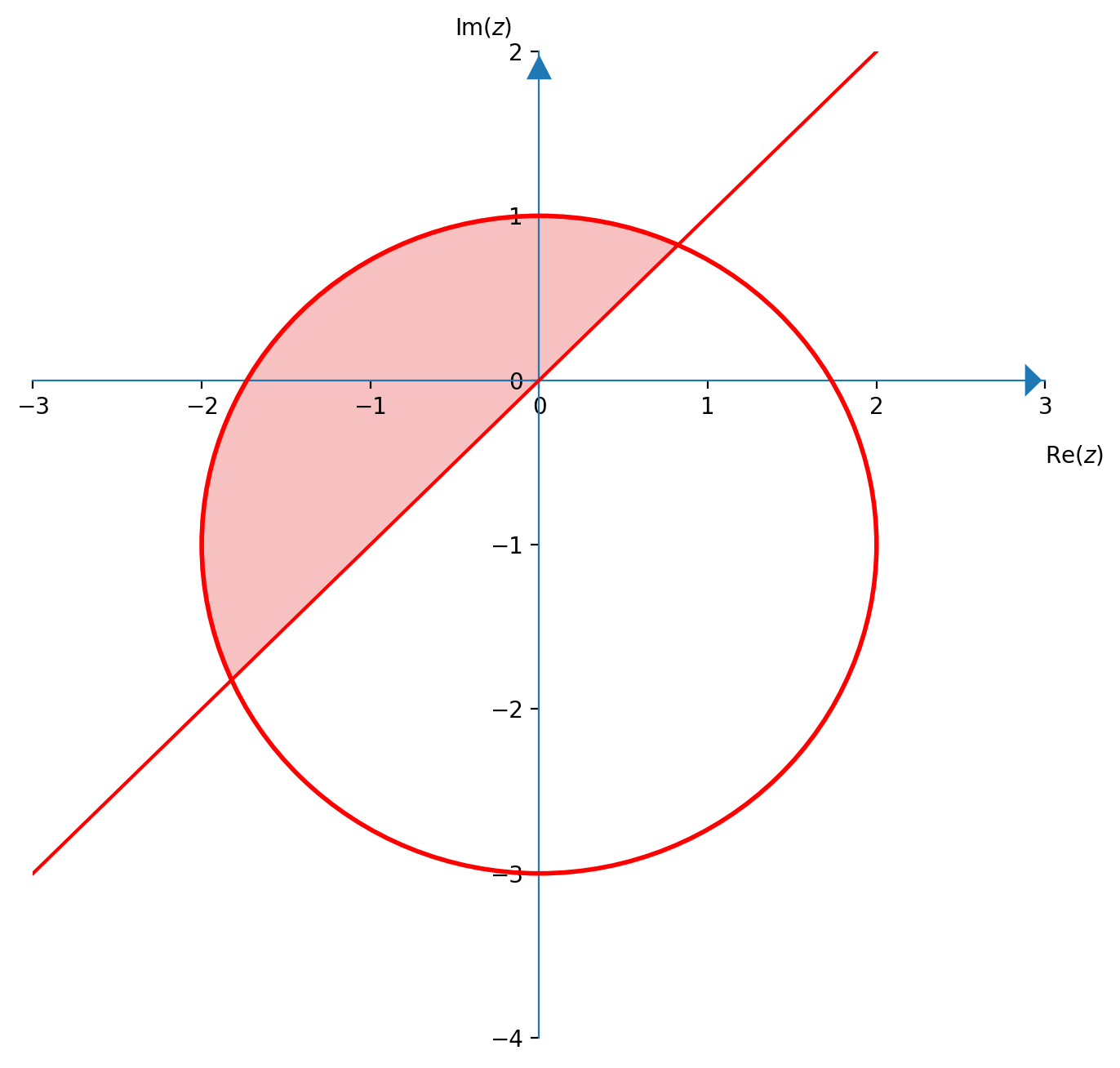
Soluzione finale

Intersecando le due condizioni $y \geqslant x$ e $\left|z+i\right|\leqslant2$ si ha l'area rappresentata in figura

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).