Luoghi geometrici notevoli (mondo complesso)

Obiettivo (corso Analisi Matematica 1)

• Luoghi geometrici notevoli
  • Coordinate complesse coniugate
• Esempi notevoli
  • Retta orizzontale
  • Retta verticale
  • Circonferenza di centro $C$ e raggio $r$

Coordinate complesse coniugate

La trasformazione $${ \begin{cases} x \;=\; \operatorname{Re}(z) \;=\; {z+\overline{z}\over 2} \\ y \;=\; \operatorname{Im}(z) \;=\; {z-\overline{z}\over 2i} \end{cases}} $$ stabilisce una rappresentazione dei punti del piano $(x,y)$ attraverso il numero complesso $z=x+iy$ e il suo coniugato $\overline{z}=x-iy$

Nota: Per la notazione algebrica si preferisce la scrittura $z=x+iy$ invece della $z=a+bi$ per agevolare l'interpretazione grafica dei risultati

Esempi notevoli

Retta orizzontale

La retta orizzontale è un'equazione del tipo $$ y \;=\; c,\quad c\in\mathbb{R} $$ che espressa in coordinate complesse diventa $$ y = {z-\overline{z}\over 2i} = c \;\Longleftrightarrow\; z-\overline{z} = i2c \;\Longleftrightarrow\; {z-\overline{z} = i\operatorname{Im}{(\alpha)},\quad \alpha\in\mathbb{C}} $$

Eseguiamo la verifica. Infatti, se $z=x+iy$ e $\alpha= a+bi$ si ha $$ z-\overline{z} = i\operatorname{Im}{(\alpha)} \;\implies\; \cancel{x}+iy - (\cancel{x}-iy) = i b \;\implies\; 2\cancel{i}y=\cancel{i}b\;\implies\; y={b\over2} $$

Retta verticale

La retta verticale è un'equazione del tipo $$ x \;=\; c,\quad c\in\mathbb{R} $$ che espressa in coordinate complesse diventa $$ x = {z+\overline{z}\over 2} = c \;\Longleftrightarrow\; z+\overline{z} = 2c \;\Longleftrightarrow\; {z+\overline{z} =\operatorname{Re}{(\alpha)},\quad \alpha\in\mathbb{C}} $$

Eseguiamo la verifica. Infatti, se $z=x+iy$ e $\alpha= a+bi$ si ha $$ z+\overline{z} = \operatorname{Re}{(\alpha)} \;\implies\; x+\cancel{iy} + (x-\cancel{iy}) = a \;\implies\; 2x=a \;\implies\; x={a\over2} $$

Circonferenza di centro $C$ e raggio $r$

L'equazione $$ {\left|z-z_0\right| \;=\; r \geqslant 0} $$ rappresenta una circonferenza con centro $z_0=(x_0,y_0)$ e raggio $r$

Infatti, posto $z=x+iy$ ed elevando al quadrato si ha $$ \left|z-z_0\right|^2 = r^2 \;\Longleftrightarrow\; (x-x_0)^2 + (y-y_0)^2 = r^2 $$

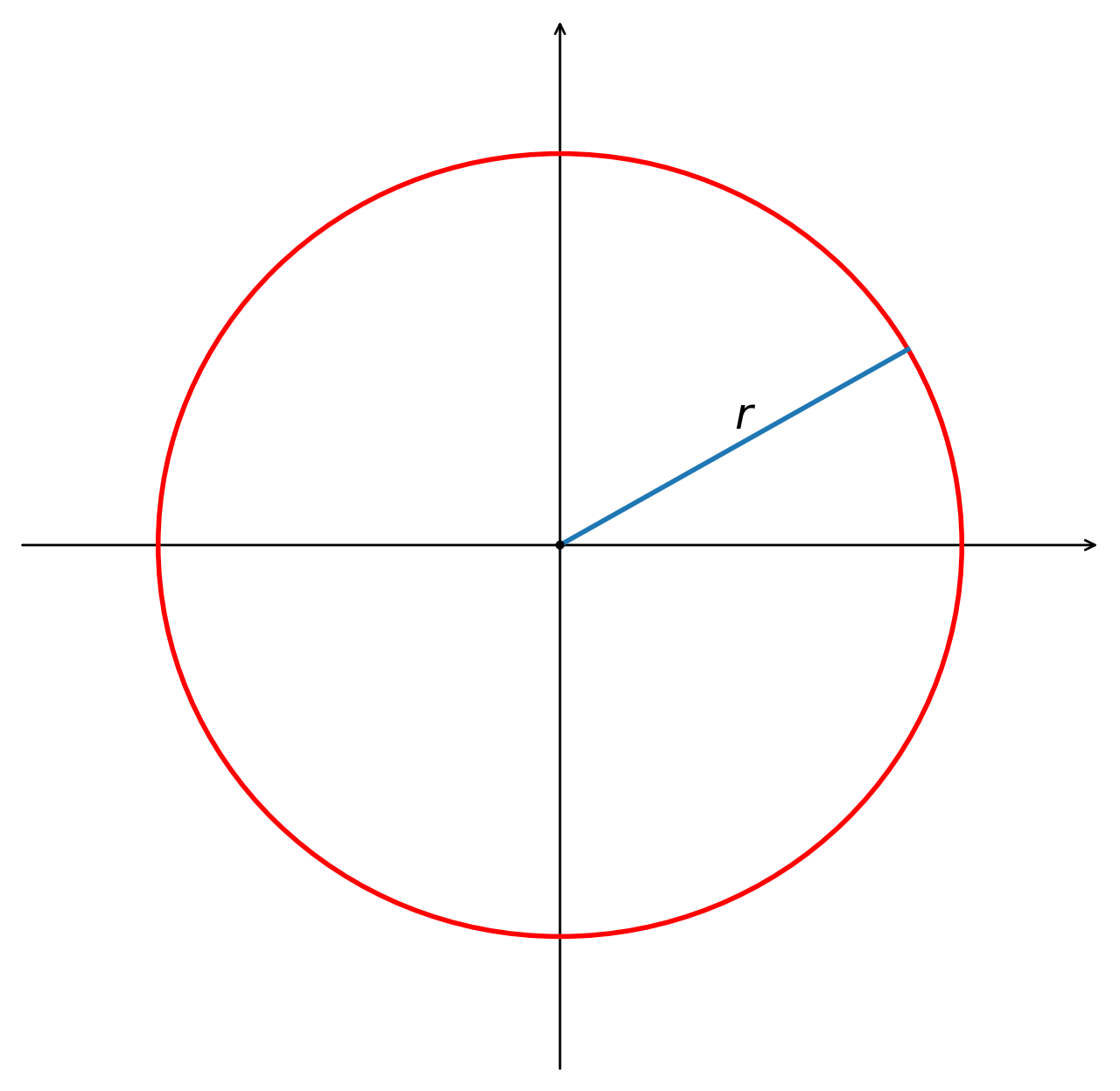
Un'altra forma è la seguente.

Da $\left|z-z_0\right| = r \geqslant 0$, possiamo scrivere $$ \left|z-z_0\right|^2 = r^2 \;\Longleftrightarrow\; (z-z_0) \cdot \overline{(z-z_0)} = r^2 \;\Longleftrightarrow\; (z-z_0) \cdot (\overline{z}-\overline{z_0}) = r^2 $$ da cui $$ z \overline{z} - \overline{z_0} z - z_0 \overline{z} + z_0 \overline{z_0} = r^2 \;\Longleftrightarrow\; {z \overline{z} - \overline{z_0} z - z_0 \overline{z} = c^2} $$ dove $c^2= r^2 - \left|z_0\right|^2$

Esempi

Esempio 1

Rappresentare le rette

1. $z+\overline{z}=\operatorname{Re}{\left(1-2i\right)}$ e
2. $z-\overline{z}=i\operatorname{Im}{\left(1-2i\right)}$

Soluzione

Posto $z=x+iy$ si ha

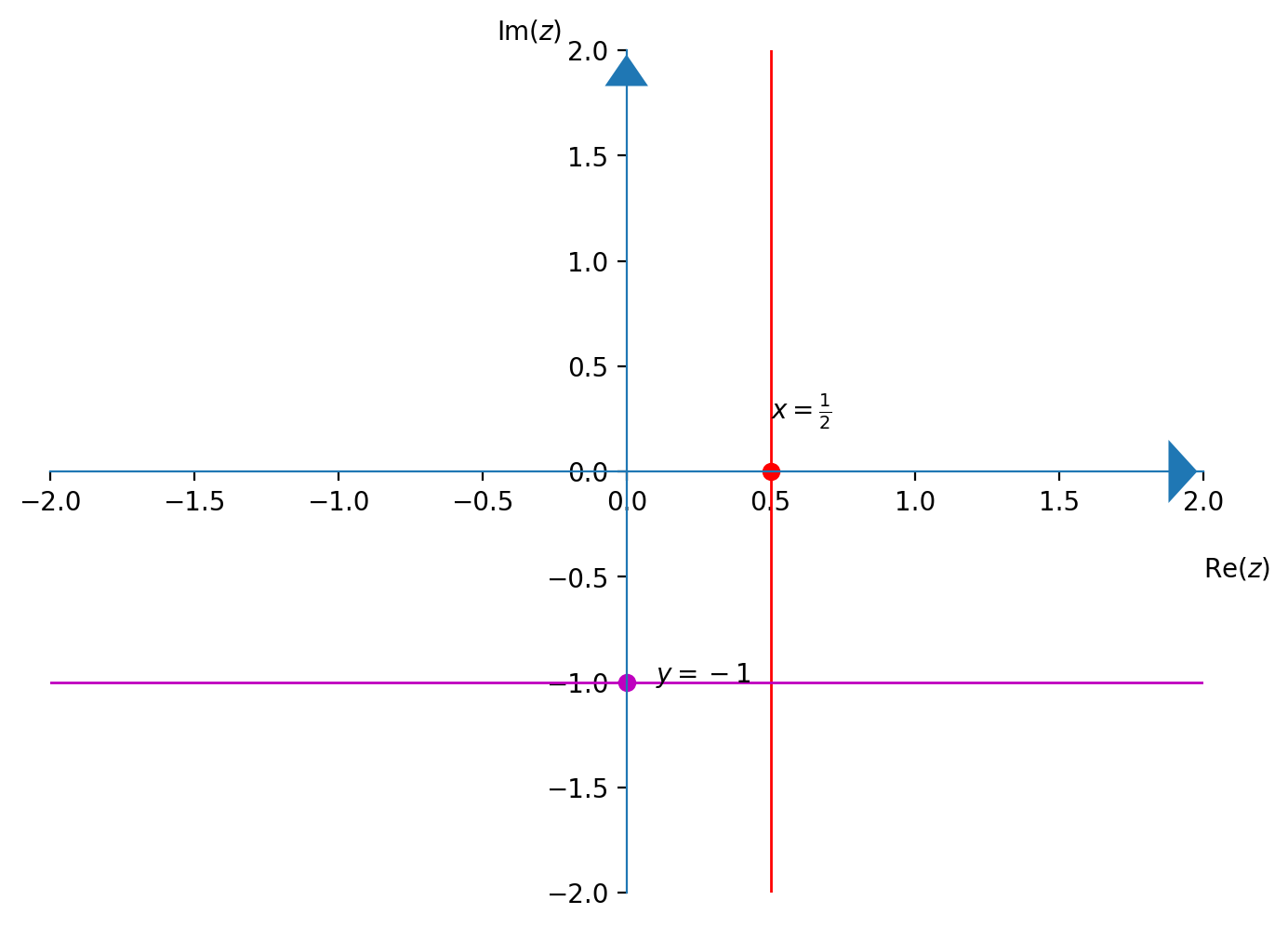
• $z+\overline{z} = 2x$ da cui $2x=1\;\implies\; x= {1\over2}$
• $z-\overline{z} = 2iy$ da cui $2iy = i\cdot (-2) \;\implies\; y = -1$

Esempio 2

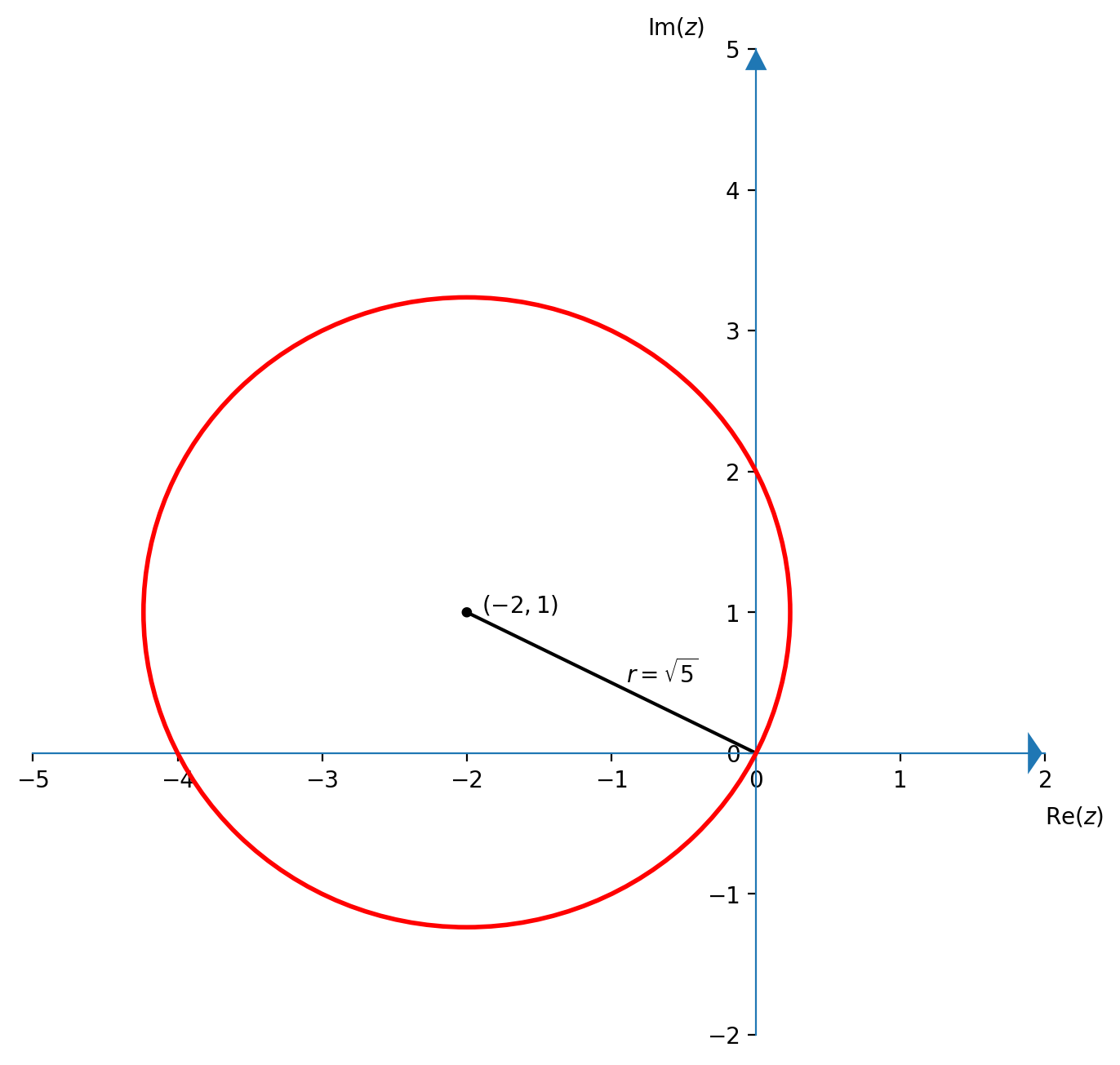
Scrivere l'equazione della circonferenza di centro $C=(-2,1)$ e passante per l'origine

Soluzione

Posto $z_0 = -2+i$, il raggio della circonferenza è $$ r = \left|z_0\right| \;=\; \sqrt{4+1} \;=\; \sqrt{5} $$ Quindi, l'equazione della circonferenza è $$ \left|z-z_0\right| \;=\; \sqrt{5} $$

Esempio 3

Descrivere il luogo geometrico $\operatorname{Re}{\left(z^2\right)}=k^2$ con $k\in\mathbb{R}$

Soluzione

Posto $z=x+iy$ si ha $$ \begin{gathered} \operatorname{Re}{\left(z^2\right)}=k^2 \;\implies\; \operatorname{Re}{\left((x+iy)^2\right)}=k^2 \;\implies\; \operatorname{Re}{\left(x^2-y^2+i2xy\right)}=k^2 \\ \;\implies\; x^2-y^2 = k^2 \;\implies\; {x^2 \over k^2} - {y^2 \over k^2} = 1 \end{gathered} $$

Rappresenta l'equazione di un'iperbole

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).