Esercizi parte 2 sui numeri complessi 2/2

Indice degli esercizi (corso Analisi Matematica 1)

1. Risolvere $\quad z^4+16=0$
2. Risolvere $\quad 2(z-1)^3-16=0$
3. Risolvere l'equazione $z^3=i$, visualizzare le soluzioni e scrivere la relativa fattorizzazione

1. Dimostrare che $\quad\cos(5x) = 5 \cos{x}\sin^4{x} -10 \cos^3{x}\sin^2{x} + \cos^5{x}$
2. Dimostrare che $\quad\sin{(4x)} = 4\cos^3{x}\sin{x} - 4\cos{x}\sin^3{x}$
3. Dimostrare che $\quad\sin^4{x} = {1\over8}\left(-4\cos{(2x)}+\cos{(4x)}+3\right)$

Soluzione

Esercizio 1

Risolvere

$$z^4+16=0$$

Soluzione

Da $z^4+16 = 0$ si ha $z^4 = -16 = 16\operatorname{cis}{(\pi)}$

Le radici $z_k$ sono $$ z_{k} \;=\; 16^{1\over 4} \operatorname{cis}{\left({\pi + 2k\pi\over4}\right)},\quad k=0,1,2,3 $$ i.e.

• $z_0 \;=\; 2\operatorname{cis}{{\pi\over4}} \;=\; 2\left({\sqrt{2}\over 2} + {\sqrt{2}\over 2}i \right) \;=\; \sqrt{2}(1+i)$
• $z_1 \;=\; 2\operatorname{cis}{3\pi\over4} \;=\; 2\left(-{\sqrt{2}\over 2} + {\sqrt{2}\over 2}i\right) \;=\; \sqrt{2}(-1+i)$
• $z_2 \;=\; 2\operatorname{cis}{{5\pi\over4}} \;=\; 2\operatorname{cis}{\left(-{3\pi\over4}\right)} \;=\; \sqrt{2}(-1-i)$
• $z_3 \;=\; 2\operatorname{cis}{{7\pi\over4}} \;=\; 2\operatorname{cis}{\left(-{\pi\over4}\right)} \;=\; \sqrt{2}(1-i)$

Esercizio 2

Risolvere

$$2(z-1)^3-16=0$$

Soluzione

Posto $u = z-1$ l'equazione $2(z-1)^3-16 = 0$ diventa $u^3 = 8$

Da $8 = 8\operatorname{cis}{(0)}$ si hanno le radici: $$ u_{k} \;=\; 8^{1\over 3} \cdot \operatorname{cis}{\left({0+k2\pi\over3}\right)},\quad k=0,1,2 $$ cioè

• $u_0 = 2 \;\implies\; z_0 = 2+1 = 3$
• $u_1 = 2\left(-{1\over 2}+i{\sqrt{3}\over 2}\right) = -1 + \sqrt{3}i \;\implies\; z_1 = -1 + \sqrt{3}i +1 = \sqrt{3}i$
• $u_2 = 2\left(-{1\over 2}-i{\sqrt{3}\over 2}\right) = -1 - \sqrt{3}i \;\implies\; z_2 = -1 - \sqrt{3}i +1 = -\sqrt{3}i$

Esercizio 3

Risolvere l'equazione $z^3 = i$, visualizzare le soluzioni e scrivere la relativa fattorizzazione

Soluzione

Da $i = \operatorname{cis}{\left({\pi\over2}\right)}$ si ha $$ z_k \;=\; \operatorname{cis}{\left({{\pi\over2}+k2\pi\over 3}\right)} \;=\; \operatorname{cis}{\left({\pi+k4\pi\over 6}\right)},\quad k=0,1,2 $$

• $z_0 \;=\; \operatorname{cis}{\left({\pi\over6}\right)} \;=\; {\sqrt{3}\over 2}+{1\over2}i$
• $z_1 \;=\; \operatorname{cis}{\left({5\pi\over6}\right)} \;=\; -{\sqrt{3}\over 2}+{1\over2}i$
• $z_2 \;=\; \operatorname{cis}{\left({9\pi\over6}\right)} \;=\; \operatorname{cis}{\left({3\pi\over2}\right)} = -i$

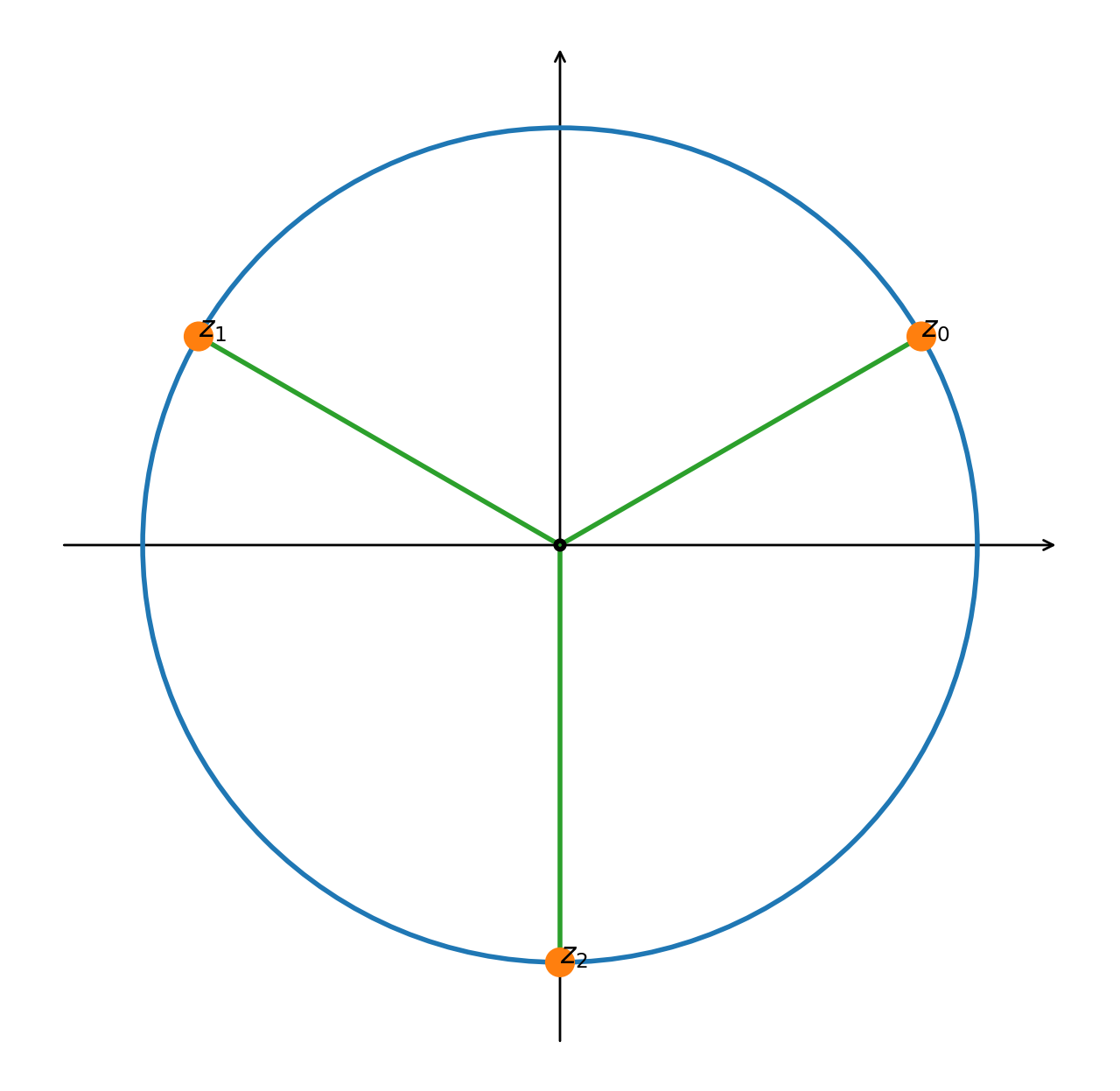
Si ha la seguente fattorizzazione

Esercizio 4

Dimostrare che

$$\cos(5x) = 5 \cos{x}\sin^4{x} -10 \cos^3{x}\sin^2{x} + \cos^5{x}$$

Soluzione

Si ha $$ \begin{aligned} \cos{(5x)} &= \operatorname{Re}{\left(e^{i5x}\right)} \\ &= \operatorname{Re}{\left(\left(e^{ix}\right)^5\right)} \\ &= \operatorname{Re}{\left(\left(\cos{x}+i\sin{x}\right)^5\right)} \\ &= \operatorname{Re} \left(\cos^5{x} +5 i\cos^4{x}\sin{x} -10 \cos^3{x}\sin^2{x} \right.\\ &\quad \left. -10i \cos^2{x}\sin^3{x} +5 \cos{x}\sin^4{x} + i\sin^5{x}\right) \\ &= \cos^5{x} -10 \cos^3{x}\sin^2{x} +5 \cos{x}\sin^4{x} \end{aligned} $$

Esempio 5

Dimostrare che

$$\sin{(4x)} = 4\cos^3{x}\sin{x} - 4\cos{x}\sin^3{x}$$

Soluzione

Si ha $$ \begin{aligned} \sin{(4x)} &= \operatorname{Im}{\left(e^{i4x}\right)} \\ &= \operatorname{Im}{\left(\left(e^{ix}\right)^4\right)} \\ &= \operatorname{Im}{\left(\left(\cos{x}+i\sin{x}\right)^4\right)} \\ &= \operatorname{Im}{\left(\cos^4{x} + 4i\cos^3{x}\sin{x} -6\cos^2{x}\sin^2{x} - 4i\cos{x}\sin^{3}{x} +\sin^4{x}\right)} \\ &= 4\cos^3{x}\sin{x} - 4\cos{x}\sin^{3}{x} \end{aligned} $$

Esempio 6

Dimostrare che

$$\sin^4{x} = {1\over8}\left(-4\cos{(2x)}+\cos{(4x)}+3\right)$$

Soluzione

Si ha $$ \begin{aligned} \sin^4{x} &= \left({e^{ix}-e^{-ix}\over 2i}\right)^4 \;=\; {1\over 16} \left(e^{ix}-e^{-ix}\right)^4 \;=\; {1\over 16} \left(e^{4ix}-4e^{2ix}+6-4e^{-2ix}+e^{-4ix}\right) \\ &= {1\over 8}\left({e^{4ix}+e^{-4ix}\over 2}\right) -{4\over8}\left({e^{2ix}+e^{-2ix}\over2}\right) + {6\over 16} \\ &= {1\over 8} \left(\cos{(4x)} -4\cos{(2x)} +3\right) \end{aligned} $$

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).