Esercizi parte 2 sui numeri complessi 1/

Indice degli esercizi (corso Analisi Matematica 1)

Scrivere in forma trigonometrica ed esponenziale i seguenti numeri complessi (espressi in forma algebrica) $$z = -1+\sqrt{3}i \quad,\quad z = -\sqrt{2}i \quad,\quad z = {\sqrt{3}\over 2} - {3\over2}i \quad,\quad z = -\sqrt{3}-i$$
Scrivere in forma trigonometrica e algebrica i seguenti numeri complessi (espressi in forma esponenziale) $$z = -34e^{\left(i{\pi\over2}\right)} \quad,\quad z = \sqrt{2}e^{\left(-i{3\pi\over4}\right)} \quad,\quad z = -2e^{\left(i{\pi\over3}\right)} \quad,\quad z = 4e^{\left(-i{\pi\over2}\right)}$$
Calcolare $\left(\sqrt{3}+i\right)^6$ e $\left(\sqrt{3}+i\right)^{-6}$
Trovare le radici seste di $1$ e rappresentarle graficamente
Trovare le radici ottave di $1$ e rappresentarle graficamente

Soluzione

Esercizio 1

Scrivere in forma trigonometrica ed esponenziale i seguenti numeri complessi (espressi in forma algebrica)

$z = -1+\sqrt{3}i$

$z = -\sqrt{2}i$

$z = {\sqrt{3}\over 2} - {3\over2}i$

$z = -\sqrt{3}-i$

Soluzione

Ricordiamo che

Forma algebrica $\Longrightarrow$ Forma trigonometrica $\Longrightarrow$ Forma esponenziale

Soluzione 1

Da $z = -1+\sqrt{3}i$ si ha

$\left|z\right| \;=\; \sqrt{1+3} = 2$
$z\in\operatorname{II}\;\operatorname{quadrante}$
$\theta \;=\; \arg{z} \;=\; \arctan{\left(-\sqrt{3}\right)} \;=\; -{\pi\over3} + \pi \;=\; {2\pi\over3}$
$z \;=\; 2\operatorname{cis}{\left({2\pi\over3}\right)} \;=\; 2 e^{\left(i{2\pi\over3}\right)}$

Soluzione 2

Da $z = -\sqrt{2}i$ si ha

$\left|z\right| \;=\; \sqrt{2}$
$z$ è immaginario puro (negativo)
$\theta \;=\; \arg{z} \;=\; -{\pi\over2}$
$z \;=\;\sqrt{2}\operatorname{cis}{\left(-{\pi\over2}\right)} \;=\; \sqrt{2}e^{\left(-i{\pi\over2}\right)}$

Soluzione 3

Da $z = {\sqrt{3}\over 2} - {3\over2}i$ si ha

$\left|z\right|\;=\; \sqrt{{3\over 4} + 9\over 4} \;=\; \sqrt{3}$
$z\in\operatorname{IV}\;\operatorname{quadrante}$
$\theta \;=\; \arg{z} \;=\; \arctan{\left({{3\over2}\over{\sqrt{3}\over 2}}\right)} \;=\; \arctan{\left(\sqrt{3}\right)} \;=\; {\pi\over3}$
$z \;=\; \sqrt{3}\operatorname{cis}{\left({\pi\over3}\right)} \;=\; \sqrt{3}e^{\left(i{\pi\over3}\right)}$

Soluzione 4

Da $z = -\sqrt{3}-i$ si ha

$\left|z\right|\;=\; \sqrt{3+1} = 2$
$z\in\operatorname{III}\;\operatorname{quadrante}$
$\theta \;=\; \arg{z} \;=\; \arctan{\left({1\over\sqrt{3}}\right)} \;=\; {\pi\over6} - \pi \;=\; -{5\pi\over6}$
$z \;=\; 2\operatorname{cis}{\left(-{5\pi\over6}\right)} \;=\; 2e^{\left(-i{5\pi\over6}\right)}$

Esercizio 2

Scrivere in forma trigonometrica e algebrica i seguenti numeri complessi (espressi in forma esponenziale)

$z = -34e^{\left(i{\pi\over2}\right)}$

$z = \sqrt{2}e^{\left(-i{3\pi\over4}\right)}$

$z = -2e^{\left(i{\pi\over3}\right)}$

$z = 4e^{\left(-i{\pi\over2}\right)}$

Soluzione

Ricordiamo che

Forma esponenziale $\Longrightarrow$ Forma trigonometrica $\Longrightarrow$ Forma algebrica

Soluzione 1

$z \;=\; -3e^{i{\pi\over2}} \;=\; -3\operatorname{cis}{{\pi\over2}} \;=\; -3( 0 + i) \;=\; -3i$

Soluzione 2

$z \;=\; \sqrt{2}e^{-i{3\pi\over4}} \;=\; \sqrt{2}\operatorname{cis}{\left(-{3\pi\over4}\right)} \;=\; \sqrt{2}\left(-{\sqrt{2}\over2}-{\sqrt{2}\over2}i\right) \;=\; -1-i$

Soluzione 3

$z \;=\; -2e^{i{\pi\over3}} \;=\; -2\operatorname{cis}{{\pi\over3}} \;=\; -2\left({1\over2}+{\sqrt{3}\over2}i\right) \;=\; -1-\sqrt{3}i$

Soluzione 4

$z \;=\; 4e^{\left(-i{\pi\over2}\right)} \;=\; 4\operatorname{cis}{\left(-i{\pi\over2}\right)} \;=\; 4 (0 - i) \;=\; -4i$

Esercizio 3

Calcolare

$\left(\sqrt{3}+i\right)^6$

$\left(\sqrt{3}+i\right)^{-6}$

Soluzione

Posto $z=\sqrt{3}+i$ si ha

$\left|z\right| \;=\; \sqrt{3+1} \;=\; 2$
$z\in\operatorname{I}\;\operatorname{quadrante}$
$\theta \;=\; \arg{z} \;=\; \arctan{{1\over\sqrt{3}}} \;=\; \arctan{{{1\over2}\over{\sqrt{3}\over 2}}} \;=\; {\pi\over6}$
$z \;=\; 2\operatorname{cis}{{\pi\over6}}$

$$ z \;=\; 2\operatorname{cis}{{\pi\over6}} $$

si ha

$z^{6} \;=\; 2^6\operatorname{cis}{\left(6\cdot {\pi\over6}\right)} \;=\; 2^6\operatorname{cis}{\pi} \;=\; -2^{6} = -64$

$z^{-6} \;=\; 2^{-6}\operatorname{cis}{\left(-6\cdot {\pi\over6}\right)} \;=\; 2^{-6}\operatorname{cis}{-\pi} \;=\; -2^{-6} \;=\; -{1\over64}$

Poteva essere calcolata anche da $z^{-6} = {\overline{z^6}\over |z^6|^2}$, oppure notando che era un numero reale

Esercizio 4

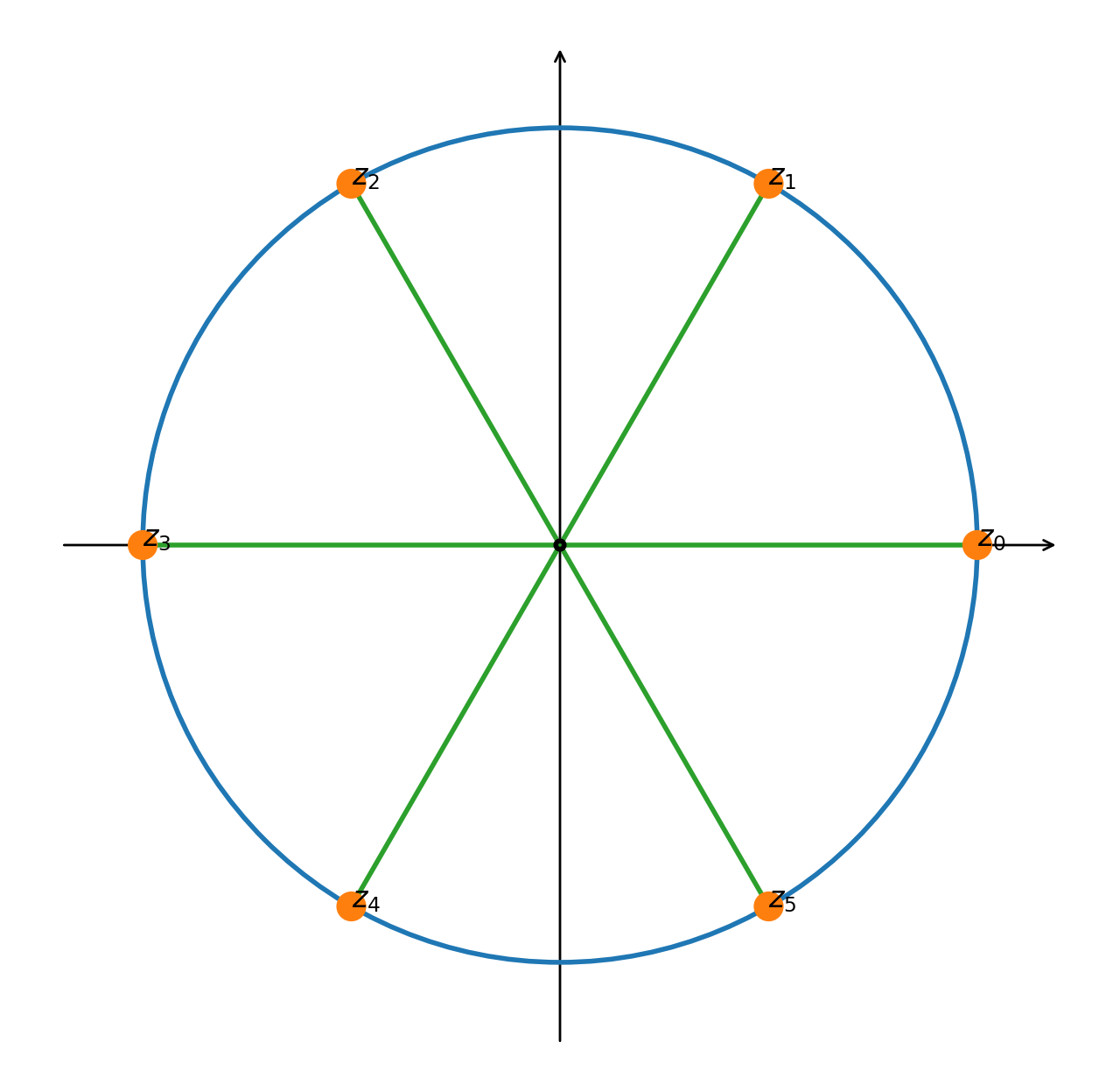
Trovare le radici seste di $1$ e rappresentarle graficamente

Soluzione

Si deve risolvere l'equazione $$ z^6 = 1 $$

Dalla forma trigonometrica $z = 1 = \operatorname{cis}{(0)}$ si ha $$ z_{k} \;=\; z^{1/6} \;=\; 1^{1\over 6} \cdot \left(\cos \left({\frac {2k\pi}{6}}\right)+i\sin \left({\frac {2k\pi }{6}}\right)\right),\quad k=0,1,\ldots, 5 $$

Le radici $z_{k}$ sono numeri complessi di modulo $1$ e argomenti multipli di ${\pi\over3}$, i.e. $$ 0, \quad {\pi\over3}, \quad {2\pi\over3}, \quad {\pi}, \quad {4\pi\over3}, \quad {5\pi\over3} $$

Per simmetria si ha

$k=0\;\implies\; z_0 = 1$
$k=1\;\implies\; z_1 = {1\over2} + {\sqrt{3}\over 2}i$
$k=2\;\implies\; z_2 = -{1\over2} + {\sqrt{3}\over 2}i$
$k=3\;\implies\; z_3 = - z_0$
$k=1\;\implies\; z_4 = - z_1$
$k=2\;\implies\; z_5 = - z_2$

Esercizio 5

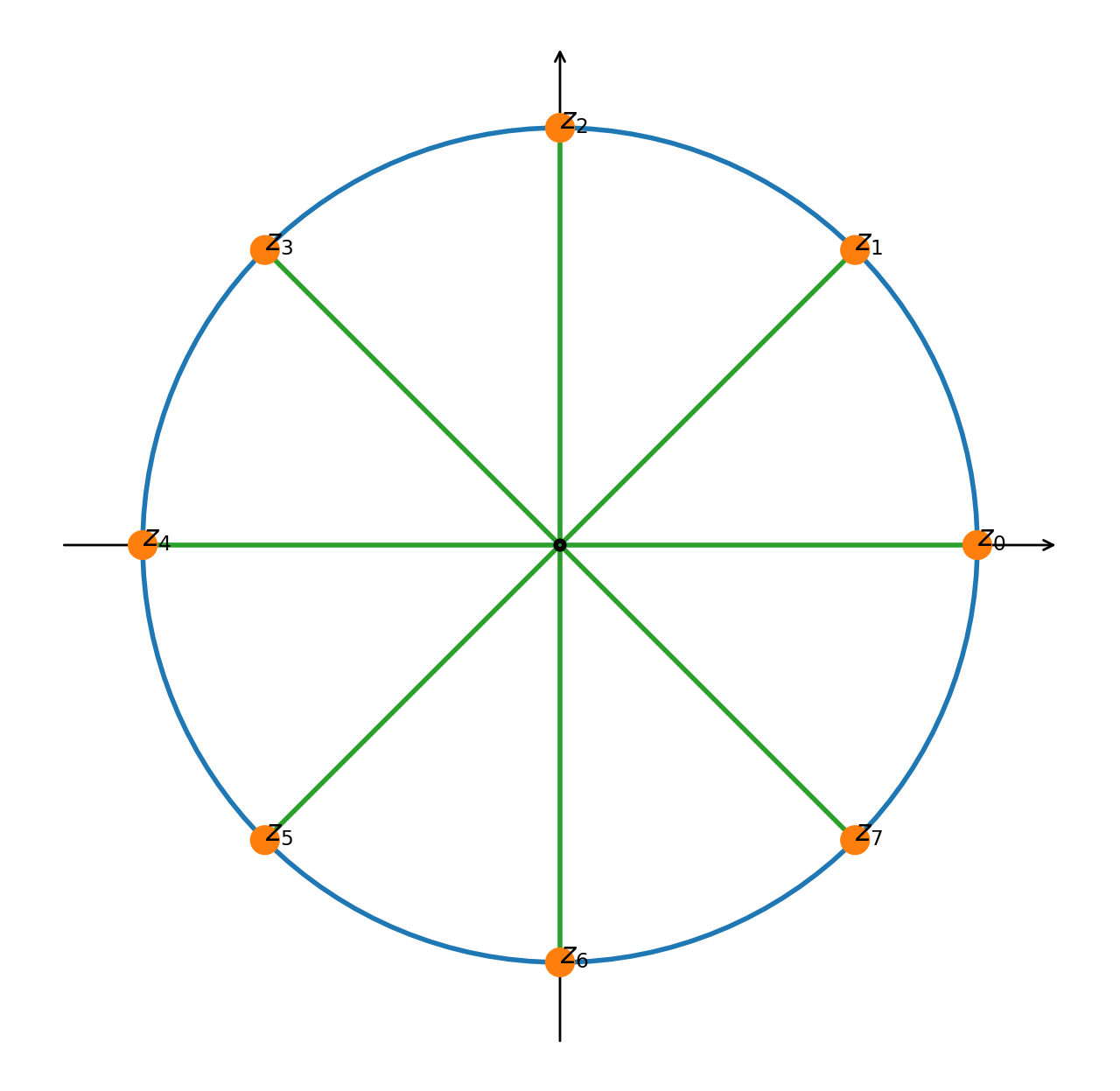
Trovare le radici ottave di $1$ e rappresentarle graficamente

Soluzione

Si deve risolvere l'equazione $$ z^8 = 1 $$

Dalla forma trigonometrica $z = 1 = \operatorname{cis}{(0)}$ si ha $$ z_{k} \;=\; z^{1/8} \;=\; 1^{1\over 8} \cdot \left(\cos \left({\frac {2k\pi}{8}}\right)+i\sin \left({\frac {2k\pi }{8}}\right)\right),\quad k=0,1,\ldots, 7 $$

Le radici $z_{k}$ sono numeri complessi di modulo $1$ e argomenti multipli di ${\pi\over4}$, i.e.

$$ 0, \quad {\pi\over4}, \quad \ldots\quad , 2\pi-{\pi\over4}={7\pi\over4} $$

Per simmetria si ha

$k=0\;\implies\; z_0 = 1$
$k=1\;\implies\; z_1 = {1\over\sqrt{2}}(1+i)$
$k=2\;\implies\; z_2 = i$
$k=4\;\implies\; z_3 = {1\over\sqrt{2}}(-1+i)$
$k=1\;\implies\; z_4 = - z_0$
$k=2\;\implies\; z_5 = - z_1$
$k=1\;\implies\; z_6 = - z_2$
$k=2\;\implies\; z_7 = - z_3$

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).