Rappresentazione esponenziale di un numero complesso

Obiettivo (corso Analisi Matematica 1)

• Forma esponenziale di un numero complesso
• Operazioni in forma esponenziale

Forma esponenziale

Definizione

Dalla definizione di esponenziale complesso $e^{a+bi}$ abbiamo la forma esponenziale di un numero complesso, i.e. $$ z \;=\; r \cdot e^{i\theta} $$ dove

• $r$ è il modulo, infatti si ha $\left|r \cdot e^{i\theta}\right| = \left|r\right| \cdot \left|e^{i\theta}\right| = r \cdot\left|\cos{\theta} + i\sin{\theta}\right| = r \cdot 1 = r$
• $\theta$ è l'argomento

Importante: La forma esponenziale di un numero complesso si deriva dalla forma trigonometrica

Operazioni in forma esponenziale

Dalla proprietà dell'esponenziale complesso segue che

• Il complesso coniugato di $z=r \cdot e^{i\theta}$ è $$ \overline{z} \;=\; r \cdot e^{-i\theta} $$

• Il prodotto di $z_1 = r_1 \cdot e^{i\theta_1}$ e $z_2 = r_2 \cdot e^{i\theta_2}$ è $$ z_1 \cdot z_2 \;=\; r_1 r_2\cdot e^{i(\theta_1 + \theta_2)} $$

• Il quoziente di $z_1 = r_1 \cdot e^{i\theta_1}$ e $z_2 = r_2 \cdot e^{i\theta_2}$è $$ {z_1 \over z_2} \;=\; {r_1 \over r_2}\cdot e^{i(\theta_1 - \theta_2)} $$

• Se $z = r \cdot e^{i\theta}$ allora la formula di De Moivre per $n\in\mathbb{N}$ diventa $$ z^{n} \;=\; r^{n}\cdot e^{in\theta} $$

• Se $z_1 = r_1 \cdot e^{i\theta_1}$ e $z_2 = r_2 \cdot e^{i\theta_2}$ allora l'argomento ha le seguenti proprietà
  • $\arg{(z_1 \cdot z_2)} \;=\; \arg{z_1} + \arg{z_2}$
  • $\arg{{z_1 \over z_2}} \;=\; \arg{z_1} - \arg{z_2}$

dove bisogna fare attenzione alla periodicità $2\pi i$ quando si usano queste ultime due formule

Interpretazione geometrica della moltiplicazione / divisione

Se $z_1 = r_1 \cdot e^{i\theta_1}$ e $z_2 = r_2 \cdot e^{i\theta_2}$ allora $$ z_1 \cdot z_2 \;=\; r_1 r_2\cdot e^{i(\theta_1 + \theta_2)} $$

Quindi, moltiplicare il numero $z_1$ per $z_2$ significa:

• Applicare una dilatazione ($r_2>1$) / contrazione ($r_2<1$) di un fattore $r_2$
• Applicare una rotazione ($\theta_2>0$ in senso antiorario, $\theta_2<0$ in senso orario) di un angolo $\theta_2$

Si ha un ragionamento simile per la divisione ma con il segno meno nell'argomento

Esempi

Esempio 1

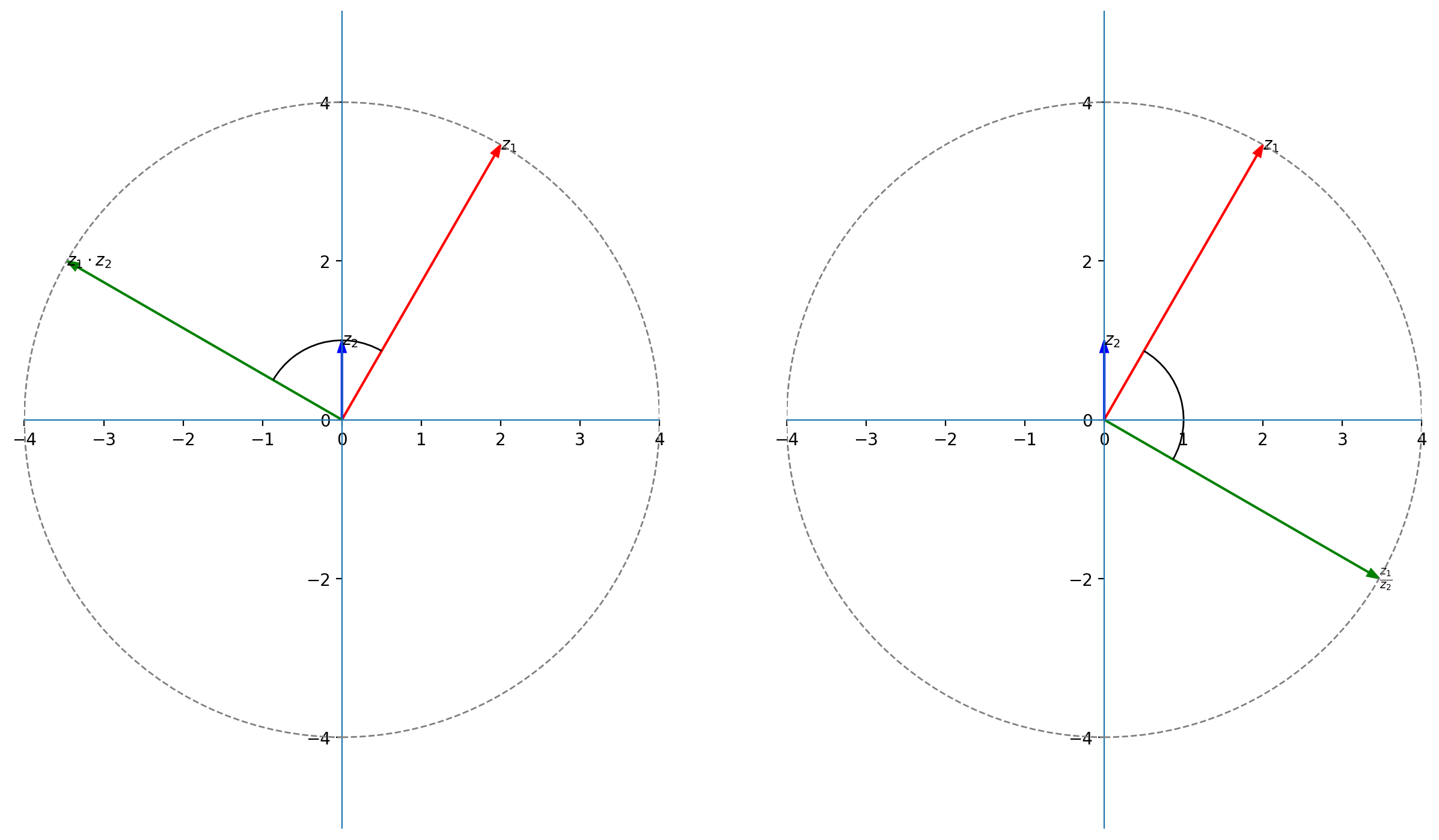
Dato $z_1 = 2+2\sqrt{3}i$ e $z_2 = i$ calcolare, utilizzando la forma esponenziale, il prodotto $z_1\cdot z_2$ e il quoziente ${z_1\over z_2}$

Soluzione

Dato

$$z_1 = 2+2\sqrt{3}i = 4e^{\left(i{\pi\over 3}\right)}\quad,\quad z_2 = i = e^{\left(i {\pi\over2}\right)}$$

si ha

• $z_1\cdot z_2 = 4e^{\left(i{\pi\over 3}\right)} \cdot e^{\left(i {\pi\over2}\right)} = 4 e^{\left(i {5\pi\over6}\right)}=-2\sqrt{3}+2i$ (rotazione di ${\pi\over2} = 90^{\circ}$)

• ${z_1\over z_2} = 4e^{\left(i{\pi\over 3}\right)} \cdot e^{\left(-i {\pi\over2}\right)} = 4 e^{\left(-i {\pi\over6}\right)}=2\sqrt{3}-2i$ (rotazione di $-{\pi\over2} = -90^{\circ}$)

Esempio 2

Dato $z_1 = 2+2\sqrt{3}i$ e $z_2 = -i$ calcolare, utilizzando la forma esponenziale, il prodotto $z_1\cdot z_2$ e il quoziente ${z_1\over z_2}$

Soluzione

Dato

$$z_1 = 2+2\sqrt{3}i = 4e^{\left(i{\pi\over 3}\right)}\quad,\quad z_2 = -i = e^{\left(-i {\pi\over2}\right)}$$

si ha

• $z_1\cdot z_2 = 4e^{\left(i{\pi\over 3}\right)} \cdot e^{\left(-i {\pi\over2}\right)} = 4 e^{\left(-i {\pi\over6}\right)}=2\sqrt{3}-2i$ (rotazione di $-{\pi\over2} = -90^{\circ}$)

• ${z_1\over z_2} = 4e^{\left(i{\pi\over 3}\right)} \cdot e^{\left(i {\pi\over2}\right)} = 4 e^{\left(i {5\pi\over6}\right)} =-2\sqrt{3}+2i$ (rotazione di ${\pi\over2} = +90^{\circ}$)

Esempio 3

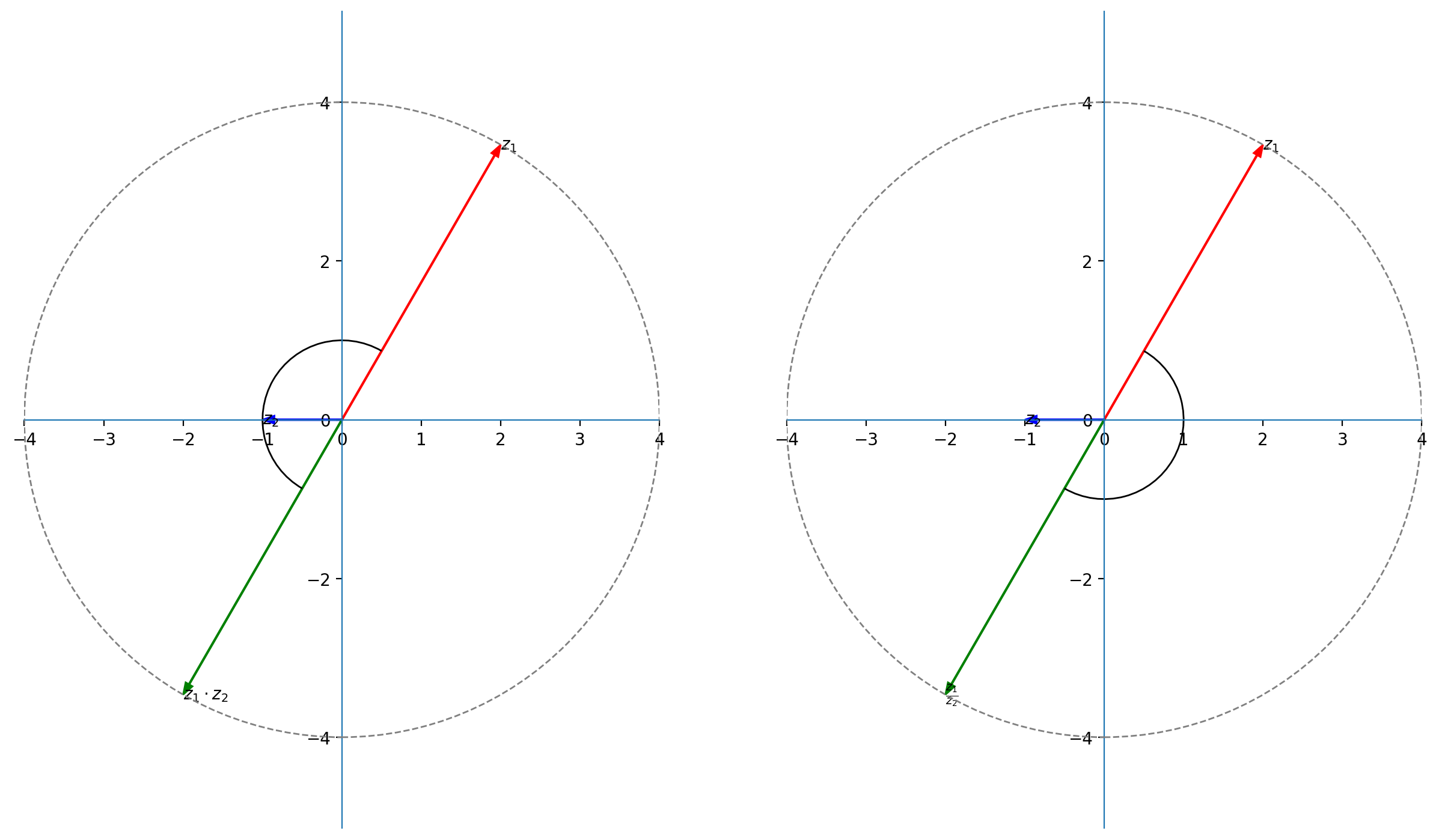
Dato $z_1 = 2+2\sqrt{3}i$ e $z_2 = -1$ calcolare, utilizzando la forma esponenziale, il prodotto $z_1\cdot z_2$ e il quoziente ${z_1\over z_2}$

Soluzione

Dato

$$z_1 = 2+2\sqrt{3}i = 4e^{\left(i{\pi\over 3}\right)}\quad,\quad z_2 = -1 = e^{(i \pi)}$$

si ha

• $z_1\cdot z_2 = 4e^{\left(i{\pi\over 3}\right)} \cdot e^{(i \pi)} = 4 e^{\left(-i {4\pi\over3}\right)}=-2-2\sqrt{3}i$ (rotazione di $\pi = 180^{\circ}$)

• ${z_1\over z_2} = 4e^{\left(i{\pi\over 3}\right)} \cdot e^{(-i \pi)} = 4 e^{\left(-i {2\pi\over3}\right)} =-2-2\sqrt{3}i$ (rotazione di $-\pi = -180^{\circ}$)

Esempio 4

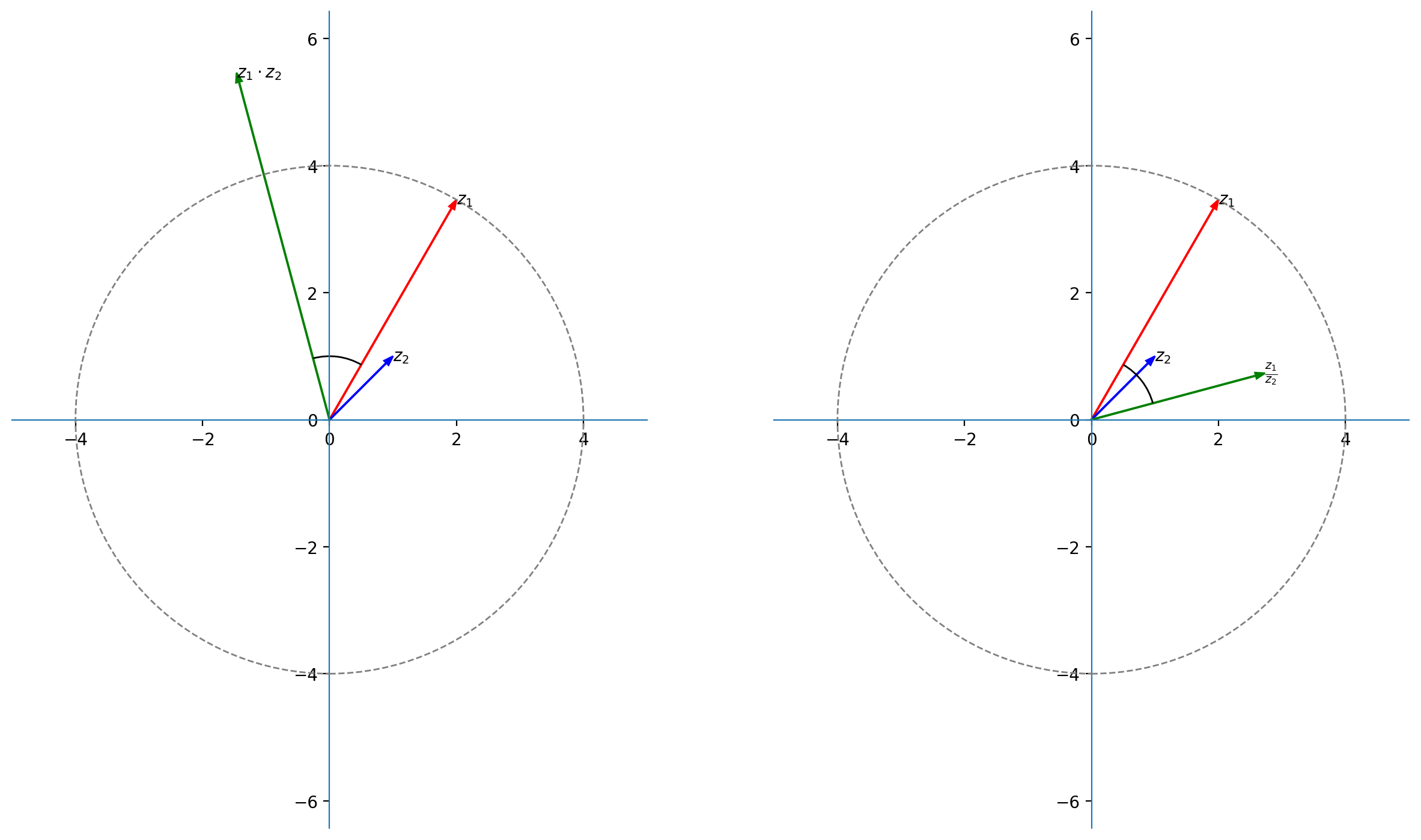
Dato $z_1 = 2+2\sqrt{3}i$ e $z_2 = 1+i$ calcolare, utilizzando la forma esponenziale, il prodotto $z_1\cdot z_2$ e il quoziente ${z_1\over z_2}$

Soluzione

Dato

$$z_1 = 2+2\sqrt{3}i = 4e^{\left(i{\pi\over 3}\right)}\quad,\quad z_2 = 1+i = \sqrt{2}e^{\left(i {\pi\over4}\right)}$$

si ha

• $z_1\cdot z_2 = 4e^{\left(i{\pi\over 3}\right)} \cdot \sqrt{2} e^{\left(i {\pi\over4}\right)} = 4\sqrt{2}e^{\left(i{7\pi\over 12}\right)} =(2-2\sqrt{3})+2i\left(1+\sqrt{3}\right)$
  (dilatazione di $\sqrt{2}$, rotazione di ${\pi\over4} = 45^{\circ}$)

• ${z_1\over z_2} = 4e^{\left(i{\pi\over 3}\right)} \cdot {1\over \sqrt{2}} e^{\left(-i {\pi\over4}\right)} = 2\sqrt{2}e^{\left(i{\pi\over 12}\right)} = (1+\sqrt{3})+i\left(\sqrt{3}-1\right)$
  (contrazione di $\sqrt{2}$, rotazione di $-{\pi\over4} = -45^{\circ}$)

Esempio 5

Trovare gli $n\in\mathbb{N}$ tali che

$$\left(1+\sqrt{3}i\right)^{n}$$

è un numero reale negativo

Soluzione

Da $z = 1+\sqrt{3}i = 2 e^{i{\pi\over3}}$, si ha che $z^n = 2^{n}e^{i n{\pi\over3}}$ è un numero reale negativo se $$ e^{i n{\pi\over3}} = -1 $$

Ricordando che, per la periodicità dell'esponenziale complesso $-1=e^{{i\pi}+k2\pi i}$, allora si ha $$ e^{i n{\pi\over3}} \;=\; -1 \;=\; e^{{i\pi}+k2\pi i} $$

La soluzione si ottiene risolvendo l'uguaglianza, i.e. $$ n{\pi\over3} = \pi + k2\pi \;\Longleftrightarrow\; n = 3 + 6k \quad (k\in\mathbb{Z}) $$

Le soluzioni richieste sono pertanto $n=3 + 6k$ con $k\in\mathbb{N}$

Esempio 6

Calcolare $i^i$

Soluzione

Da $i=1\cdot e^{i {\pi\over2}}$ si ha $$ i^i \;=\; \left(e^{i {\pi\over2}}\right)^i \;=\; e^{-{\pi\over2}} $$

Nota: $e^{i{\pi\over2}}$ non è la sola rappresentazione di $i$: infatti, dalla periodicità dell'esponenziale complesso si ha $i=e^{i{\pi\over2}+k2\pi i}$ con $k\in\mathbb{Z}$. Quindi, in realtà, la soluzione dipende da quale $k$ si sceglie. La scelta $k=0$, corrisponde a scegliere il ramo detto "naturale" del logaritmo complesso.

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).