Le radici n-esime di un numero complesso

Obiettivo (corso Analisi Matematica 1)

• Radici $n$-esime di un numero complesso
• Significato geometrico delle radici complesse
• Radici $n$-esime dell'unità

Radici $n$-esime di un numero complesso

Definizione

Sia $z\in\mathbb{C}$ e $n\in\mathbb{N}$ con $n>1$. In analogia con il caso reale, un numero $w\in\mathbb{C}$ è una radice $n$-esima di $z$ se $$ w^{n} \;=\; z$$

Se $z=0$ si ha una sola radice: $w=0$

Teorema fondamentale

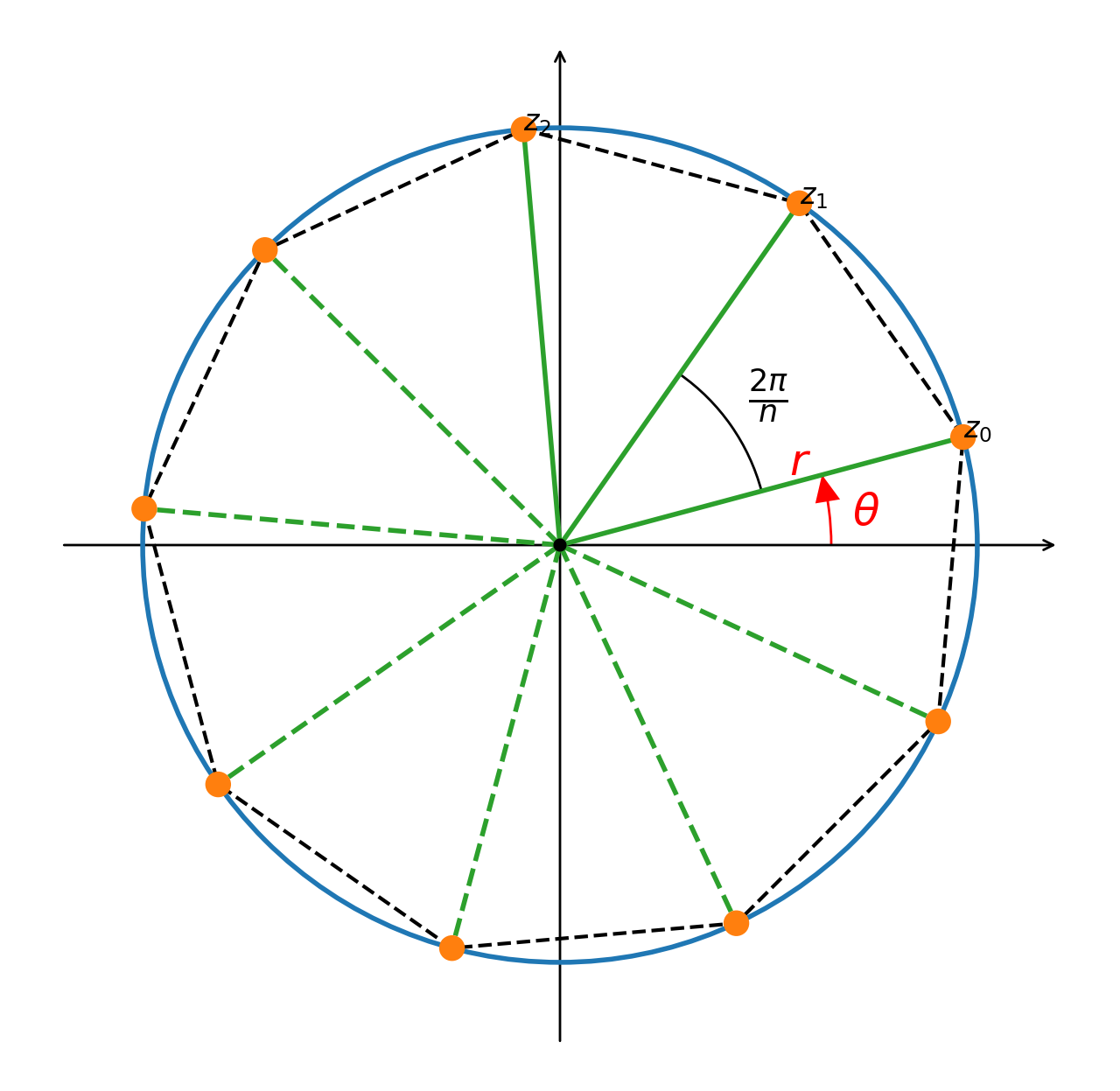
Sia $z\in\mathbb{C}$ e $n\in\mathbb{N}$ con $n>1$. Se $z\ne0$, allora $z$ ammette esattamente $n$ radici distinte e, da $z =r \operatorname{cis}\left(\theta\right)$, sono della forma

$$z_k \;=\; z^{1\over n} \;=\; r^{1\over n}\operatorname{cis}{\left({\theta+k2\pi\over n}\right)},\quad k=0,1,\ldots,n-1$$

dove due radici consecutive $z_{k}$ e $z_{k+1}$ differiscono di $2\pi\over n$

Nota:

• $\sqrt{z}$ ha due radici che sono opposte tra loro

Dimostrazione

Ricordiamo la formula di De Moivre: se $z = r\operatorname{cis}\left(\theta\right)$ allora $z^n \;=\; r^n\operatorname{cis}{(n\theta)}$

Utilizzando De Moivre, le radici sono

$$ z_k \;=\; r^{1\over n}\operatorname{cis}{\left({\theta+k2\pi\over n}\right)},\quad k=0,1,\ldots,n-1 $$

in quanto soddisfano la relazione $z_k^{n}=z$

Per dimostrare che le radici sono esattamente $n$, basta osservare che $z_{k+n} = z_{k}$, infatti

Significato geometrico delle radici complesse

Le radici n-esime rappresentano gli $n$ vertici di un poligono regolare

• con posizione iniziale $\theta=\arg{z}$
• raggio $r=\left|z\right|$
• cerchio $\left|z\right| = r \implies \operatorname{Re}(z)^2 + \operatorname{Im}(z)^2 = r^2$

Radici $n$-esime dell'unità

Le soluzioni di $$z^{n}=1$$ con $n\in\mathbb{N}$ e $n>1$ sono dette radici $n$-esime dell'unità e sono date da ($\theta=0$) $$ z_{k} \;=\; \operatorname{cis}\left({k{2\pi\over n}}\right),\quad k=0,1,\ldots,n-1 $$

Se $\omega = \operatorname{cis}\left({{2\pi\over n}}\right)$ allora le $n$ radici sono $$ 1,\ \omega,\ \omega^2,\ \ldots ,\omega^{n-1},\ $$

Per passare alla successiva radica si moltiplica per $\omega$ ovvero si somma $\frac{2\pi}{n}$ all'angolo $\theta$ della precedente

Esempi

Esempio 1

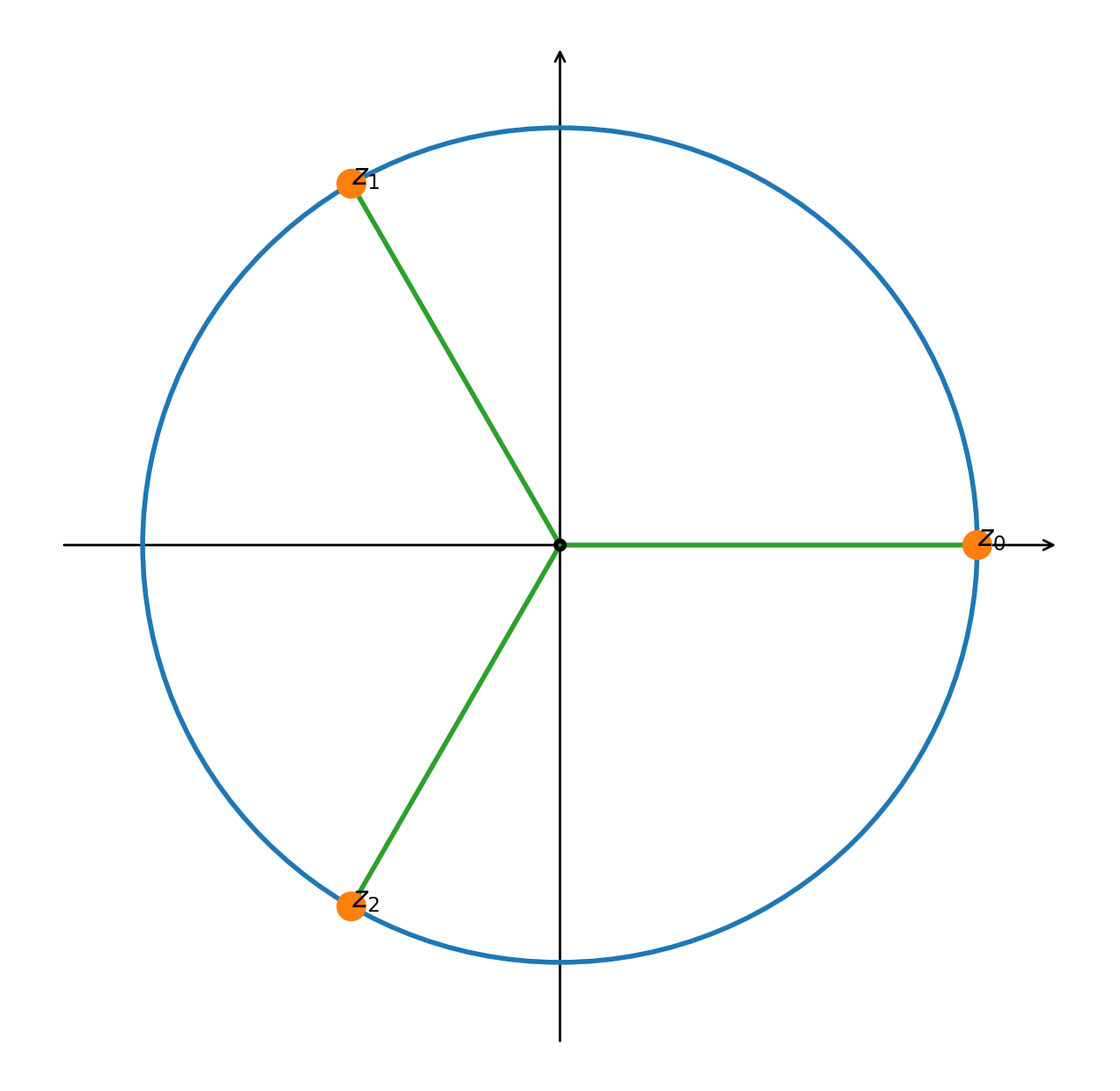
Trovare le radici cubiche di $1$

Soluzione

Si deve risolvere l'equazione $$ z^3 = 1 $$

Forma trigonometrica di $z=1$:

• $r \;=\; \left|z\right|\;=\; 1$
• $z\in\operatorname{I}\;\operatorname{quadrante}$
• $\theta \;=\; \arctan{\left({0\over1}\right)} \;=\; \arctan{0} \;=\; 0 \;=\; 0^{\circ}$
• $z \;=\; 1 \cdot \operatorname{cis}{(0)}$

Si ha $$ z_{k} \;=\; z^{1/3} \;=\; 1^{1\over 3} \cdot \left(\cos \left({\frac {2k\pi}{3}}\right)+i\sin \left({\frac {2k\pi }{3}}\right)\right),\quad k=0,1,2 $$ da cui

• $k=0\implies z_0 = 1$
• $k=1\implies z_1 = \cos \left({\frac {2\pi}{3}}\right)+i\sin \left({\frac {2\pi }{3}}\right) = -{1\over 2}+i{\sqrt{3}\over 2}$
• $k=2\implies z_2 = \cos \left({\frac {4\pi}{3}}\right)+i\sin \left({\frac {4\pi }{3}}\right) = -{1\over 2}-i{\sqrt{3}\over 2}$

Soluzione alternativa

Dalla fattorizzazione $$ z^3 = 1 \implies (z-1)(z^2+z+1)=0 $$ si ha

• $z-1 = 0 \implies z_0 = 1$
• $z^2+z+1= 0 \implies z_{1,2} = {-1\pm\sqrt{1-4}\over 2} = {-1\pm i\sqrt{3}\over 2}$

Esempio 2

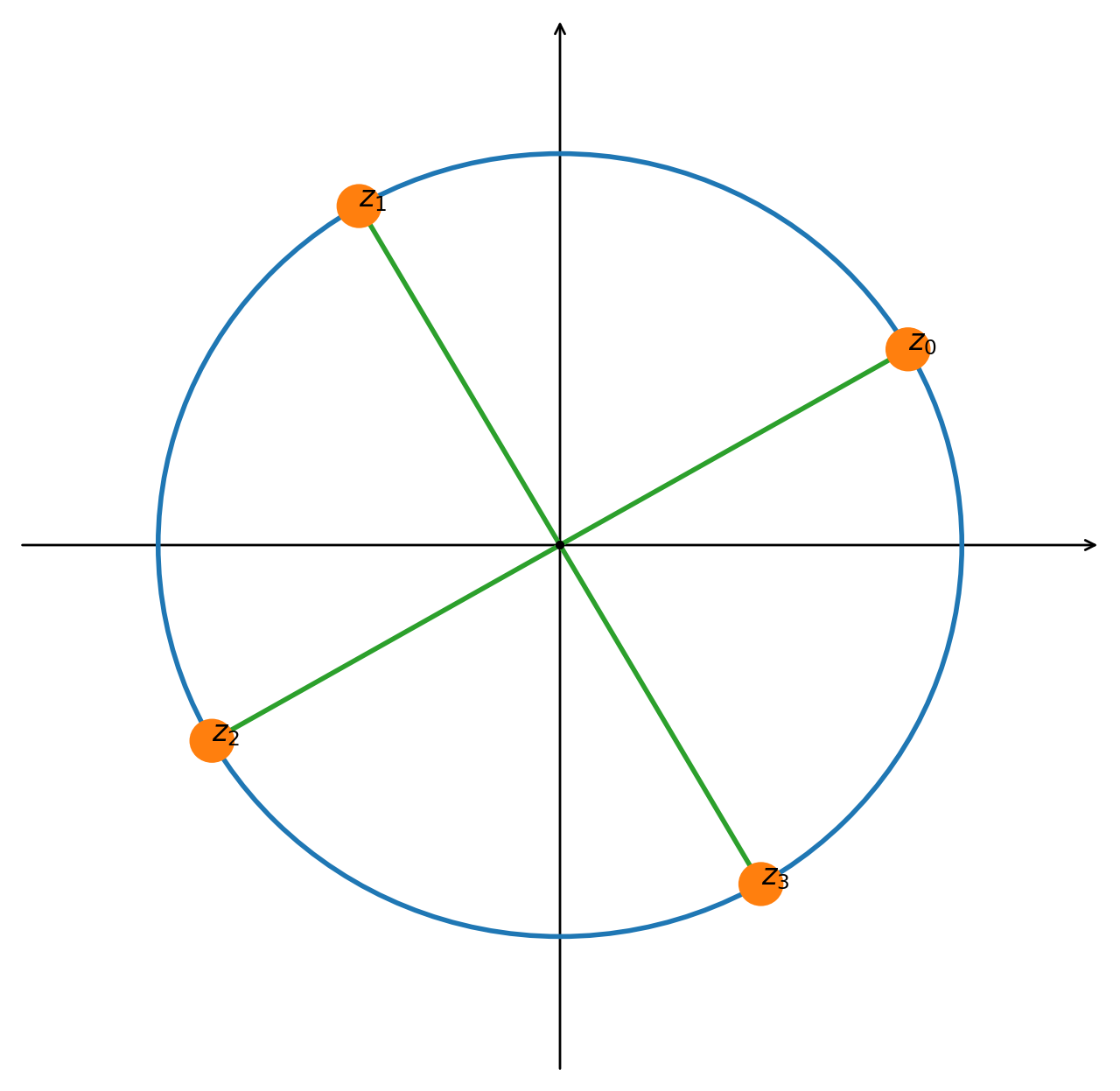
Trovare le radici quarte del numero complesso $z = 8(-1+\sqrt{3}i)$

Soluzione

Forma trigonometrica di $z=8(-1+\sqrt{3}i)$:

• $r \;=\; \left|z\right| \;=\; 8\sqrt{1+3} \;=\; 16$
• $z\in\operatorname{II}\;\operatorname{quadrante}$
• $\theta \;=\; \arctan{(-\sqrt{3})} \;=\; {2\over3}\pi = 120^{\circ}$
• $z \;=\; 16 \cdot \operatorname{cis}{\left({2\over3}\pi\right)}$

Si ha $$ z_{k} \;=\; z^{1/4} \;=\; 16^{1\over4} \operatorname{cis}{\left({{2\over3}\pi+k2\pi\over 4}\right)},\quad k=0,1,2,3 $$ da cui

• $k=0\;\implies\; z_0 = 2\left(\cos{\pi\over6}+i\sin{\pi\over6}\right) = 2\left({\sqrt{3}\over 2}+i\sin{1\over2}\right) = \sqrt{3}+i$
• $k=1\;\implies\; z_1 = -1 + i\sqrt{3}$
• $k=2\;\implies\; z_2 = -z_0$
• $k=3\;\implies\; z_3 = -z_1$

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).