Forma trigonometrica di un numero complesso
Obiettivo (corso Analisi Matematica 1)
- Rappresentazione trigonometrica di un numero complesso
- Calcolo dell'argomento / anomalia
- Dalla forma trigonometrica alla forma algebrica
- Coniugato
- Prodotto di due numeri in forma trigonometrica
- Quoziente di due numeri
Rappresentazione trigonometrica
Definizione
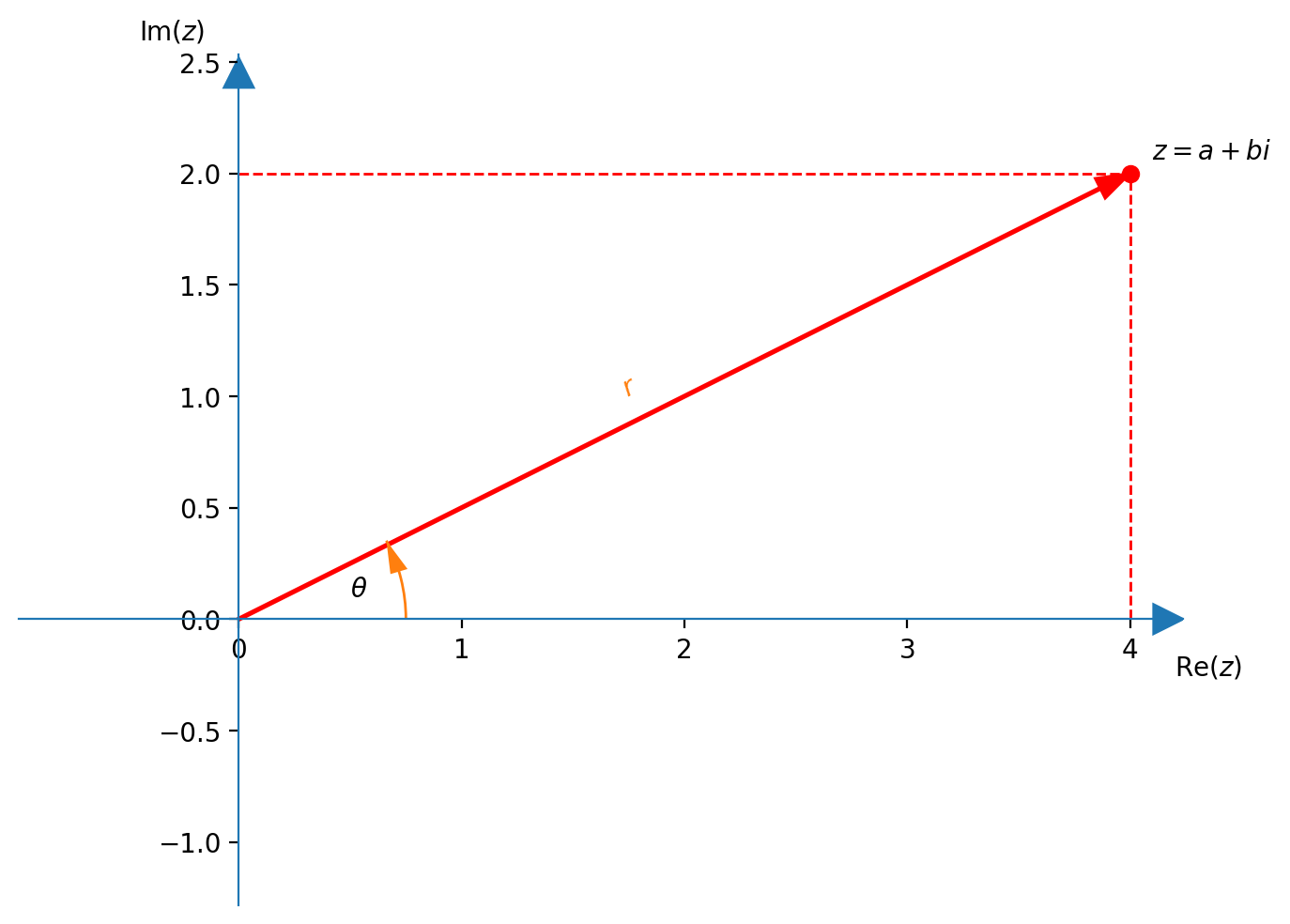
Dato il numero complesso $z=a + bi$, la sua rappresentazione trigonometrica è $$ z \;=\; r \cdot \operatorname{cis}\left(\theta\right) \;=\; r \cdot \left(\cos{\theta} + i\sin{\theta}\right) $$ dove:
- $r=\left|z\right|= \sqrt{a^2+b^2}$, con $r\geq 0$, è detto modulo o valore assoluto e rappresenta la lunghezza del vettore $z$
- $\theta=\arg{z}\in (-\pi,\pi]$ è detto argomento o anomalia e rappresenta l'angolo rispetto al semiasse di riferimento del vettore $z$
L'interpretazione grafica è riportata in figura
Alcune osservazioni:
- $-\pi < \theta \leqslant \pi$ è detto intervallo principale
- Altre scelte sono possibili come $0\leqslant \theta < 2\pi$
- Nell'esecuzione delle operazioni (es. prodotto, quoziente), l'angolo va sempre riportato nel suo intervallo di definizione
- L'obiettivo è di rendere biunivoca la corrispondenza tra forma trigonometrica e forma algebrica
- Per $z=0$ si definisce $r=0$ e $\theta=\text{non definito}$ (così la trasformazione è biunivoca)

Calcolo dell'argomento / anomalia
Dato il numero complesso $z=a + bi$, se $\theta = \arg{z}\in (-\pi,+\pi]$, si ha
$$ \begin{cases} \frac{\pi}{2} & \text{ se }a=0,\ b>0 \\ -\frac{\pi}{2} & \text{ se }a=0,\ b<0 \\ \text{non definito} & \text{ se }a=0,\ b=0 \\ \arctan{\left(\frac{b}{a}\right)} & \text{ se }a>0,\ b\text{ qualsiasi} \\ \arctan{\left(\frac{b}{a}\right)}+\pi & \text{ se }a<0,\ b\geq 0 \\ \arctan{\left(\frac{b}{a}\right)}-\pi & \text{ se }a<0,\ b< 0 \end{cases} $$

Dalla forma trigonometrica alla forma algebrica
Se $z=\operatorname{cis}\left(\theta\right)$, allora $z=a+bi$ si ottiene come
$$ \begin{cases} a = r \cdot \cos{\theta} \\ b = r \cdot \sin{\theta} \end{cases} $$

Coniugato
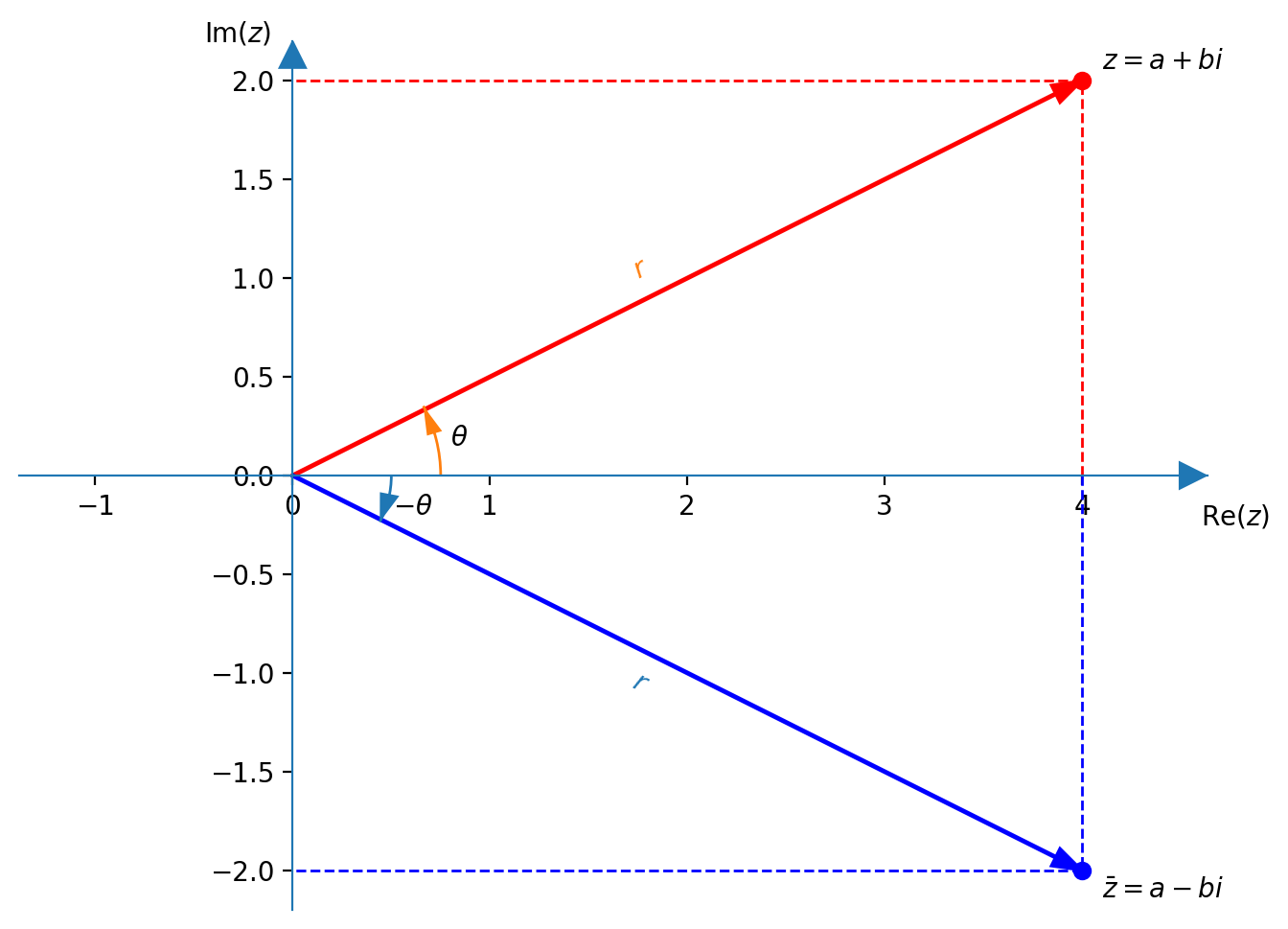
Dalla relazione $$ z = r\operatorname{cis}\left(-\theta\right) = r \left(\cos{\theta} - i \sin{\theta}\right) $$ si ha che il complesso coniugato di $z=\operatorname{cis}\left(\theta\right)$ è $$ \overline{z} = r \left(\cos{\theta} - i \sin{\theta}\right) \;=\; r\operatorname{cis}\left(-\theta\right) $$
Prodotto di due numeri in forma trigonometrica
Se $z_1 = r_1\operatorname{cis}\left(\theta_1\right)$ e $z_2 = r_2\operatorname{cis}\left(\theta_2\right)$, allora il loro prodotto è $$ z_1 \cdot z_2 = r_1 r_2\operatorname{cis}\left(\theta_1 + \theta_2\right) $$
Si ottiene come prodotto dei moduli e somma degli angoli dei due numeri
Dimostrazione
Si ha $$ \begin{aligned} z_1 \cdot z_2 &= \left[r_1\operatorname{cis}\left(\theta_1\right)\right] \cdot \left[r_2\operatorname{cis}\left(\theta_2\right)\right] \\ &= r_1 r_2 \left[\left(\cos{\theta_1}\cos{\theta_2} - \sin{\theta_1}\sin{\theta_2}\right) \right. \\ &\quad \left.+ i\left(\sin{\theta_1}\cos{\theta_2} + \cos{\theta_1}\sin{\theta_2}\right) \right] \\ &= r_1 r_2\operatorname{cis}\left(\theta_1 + \theta_2\right) \end{aligned} $$
Prodotto di due numeri in forma trigonometrica

Quoziente di due numeri
Se $z_1 = r_1\operatorname{cis}\left(\theta_1\right)$ e $z_2 = r_2\operatorname{cis}\left(\theta_2\right)$, allora il loro quoziente è $$ {z_1 \over z_2} = {r_1 \over r_2}\operatorname{cis}\left(\theta_1 - \theta_2\right) $$
Si ottiene come divisione dei moduli e differenza degli angoli dei due numeri
Dimostrazione
Si ha $$ \begin{aligned} {z_1 \over z_2} &= {r_1\operatorname{cis}\left(\theta_1\right)\over r_2\operatorname{cis}\left(\theta_2\right)} \cdot {\left(\cos{\theta_2} - i\sin{\theta_2}\right) \over \left(\cos{\theta_2} - i\sin{\theta_2}\right)} \\ &= {r_1 \over r_2} \cdot {\left(\cos{\theta_1}\cos{\theta_2} + \sin{\theta_1}\sin{\theta_2}\right) + i \left(\sin{\theta_1}\cos{\theta_2} - \cos{\theta_1}\sin{\theta_2}\right) \over \cos^{2}{\theta_2} + \sin^{2}{\theta_2}} \\ &={r_1 \over r_2}\operatorname{cis}\left(\theta_1 - \theta_2\right) \end{aligned} $$
Esempi
Esempio 1
Dato il numero complesso $z=\sqrt{3}-i$
- Scrivere la relativa forma trigonometrica
- Calcolare il coniugato
- Rappresentare i risultati graficamente
Soluzione
Da $z=\sqrt{3}-i$ si ha
- $\left|z\right| \;=\; \sqrt{\left(\sqrt{3}\right)^2+\left(-1\right)^2} \;=\; \sqrt{3+1} \;=\; \sqrt{4} \;=\; 2$
- $z\in\text{IV quadrante}$ e $\theta \;=\; \arctan{\left(-1\over \sqrt{3}\right)} \;=\; \arctan{\left(-\sqrt{3}\over 3\right)} \;=\; - {\pi\over 6} \;=\; -30^{\circ}$
- $z \;=\; 2\operatorname{cis}{\left(- {\pi\over 6}\right)}$
- $\overline{z} \;=\; 2\operatorname{cis}{\left({\pi\over 6}\right)}$
Eseguiamo la verifica
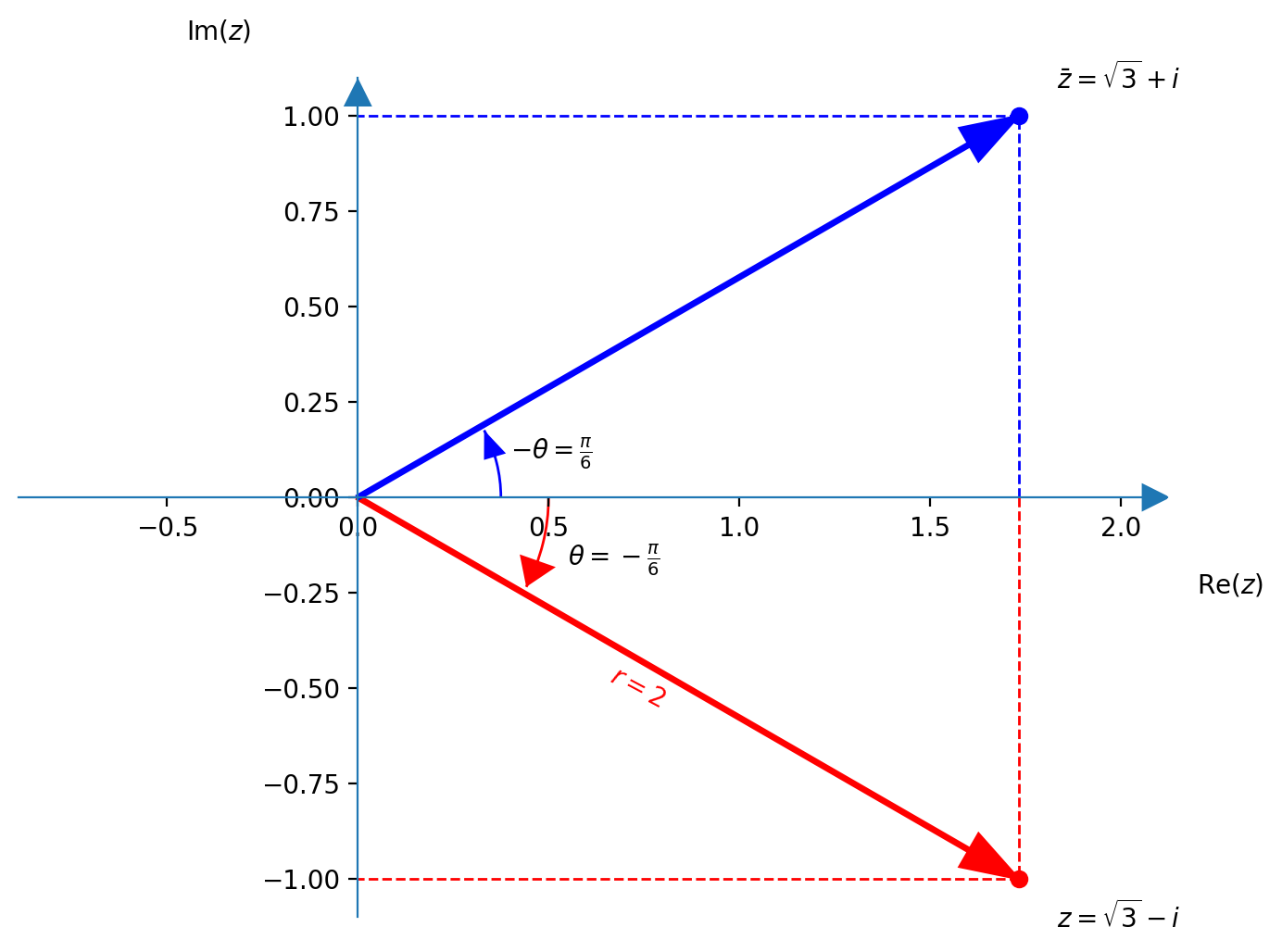
- $z \;=\; 2\operatorname{cis}{\left(-{\pi\over 6}\right)} \;=\; 2 \left({\sqrt{3} \over 2} - {1\over 2}i \right) \;=\; \sqrt{3}-i$
- $\overline{z} \;=\; 2\operatorname{cis}{\left({\pi\over 6}\right)} \;=\; 2 \left({\sqrt{3} \over 2} + {1\over 2}i \right) \;=\; \sqrt{3}+i$
Esempio 2
Dati i numeri complessi $z_1=1+\sqrt{3}i$ e $z_2=-\sqrt{3}+i$, calcolare
- $z_1 \cdot z_2$ e il relativo numero in forma algebrica
- ${z_1 \over z_2}$ e il relativo numero in forma algebrica
- rappresentare i risultati graficamente
Soluzione
La rappresentazione trigonometrica di $z_1=1+\sqrt{3}i$ è
- $\left|z_1\right| \;=\; \sqrt{1+3} = 2$
- $z\in\text{I quadrante}$
- $\theta =\arctan{\left(\sqrt{3}\over 1\right)} \;=\; \arctan{\sqrt{3}} \;=\; {\pi\over 3} \;=\; 60^{\circ}$
- $z_1 \;=\; 2\operatorname{cis}{\left({\pi\over 3}\right)}$
La rappresentazione trigonometrica di $z_2=-\sqrt{3}+i$ è
- $\left|z_2\right| \;=\; \sqrt{3+1} = 2$
- $z\in\text{II quadrante}$
- $\theta \;=\; \arctan{\left(1 \over -\sqrt{3}\right)} \;=\; \arctan{\left(-{\sqrt{3}\over 3}\right)} \;=\; \pi - {\pi\over 6} \;=\; {5\over6}\pi \;=\; 150^{\circ}$
- $z_2 \;=\; 2\operatorname{cis}\left({5\over6}\pi\right)$
Il prodotto di $z_1=1+\sqrt{3}i$ e $z_2=-\sqrt{3}+i$ è
- $z_1 \;=\; 2\operatorname{cis}{\left({\pi\over 3}\right)}$
- $z_2 \;=\; 2\operatorname{cis}{\left({5\over6}\pi\right)}$
- $z_1 \cdot z_2 \;=\; 2 \cdot 2 \operatorname{cis}\left({\pi\over 3} + {5\over6}\pi\right) \;=\; 4 \operatorname{cis}{\left({7\over6}\pi\right)} \;=\; 4 \operatorname{cis}{\left(-{5\over6}\pi\right)}$ (riportato in $(-\pi,\pi]$)
- $z_1 \cdot z_2 \;=\; 4 \operatorname{cis}{\left(-150^{\circ}\right)}$
- In forma algebrica: $z_1 \cdot z_2 \;=\; 4 \left(-{\sqrt{3}\over 2}-{1\over2}i\right) \;=\; -2\sqrt{3} -2i$
- verifica: $z_1 \cdot z_2 \;=\; (1+\sqrt{3}i) \cdot (-\sqrt{3}+i) \;=\; -\sqrt{3}-\sqrt{3} +i-3i \;=\; -2\sqrt{3} -2i$
Il prodotto di $z_1=1+\sqrt{3}i$ e $z_2=-\sqrt{3}+i$ è
- $z_1 \;=\; 2\operatorname{cis}{\left({\pi\over 3}\right)}$
- $z_2 \;=\; 2\operatorname{cis}{\left({5\over6}\pi\right)}$
- ${z_1 \over z_2} \;=\; {2 \over 2}\operatorname{cis}{\left({\pi\over 3} - {5\over6}\pi\right)} \;=\; 1\operatorname{cis}{\left({\pi\over 3} - {5\over6}\pi\right)} \;=\; \operatorname{cis}{\left(-{\pi\over2}\right)}$
- ${z_1 \over z_2} \;=\; \operatorname{cis}{\left(-90^{\circ}\right)}$
- In forma algebrica: ${z_1 \over z_2} \;=\; 0 -i \;=\; -i$
- verifica: ${z_1 \over z_2} \;=\; {1+\sqrt{3}i \over -\sqrt{3}+i} \cdot {-\sqrt{3}-i \over -\sqrt{3}-i} \;=\; {(1+\sqrt{3}i) \cdot (-\sqrt{3}-i) \over 3+1} \;=\; {-\cancel{\sqrt{3}}-i -3i+\cancel{\sqrt{3}} \over 4} \;=\; {-\cancel{4}i\over \cancel{4}} = -i$
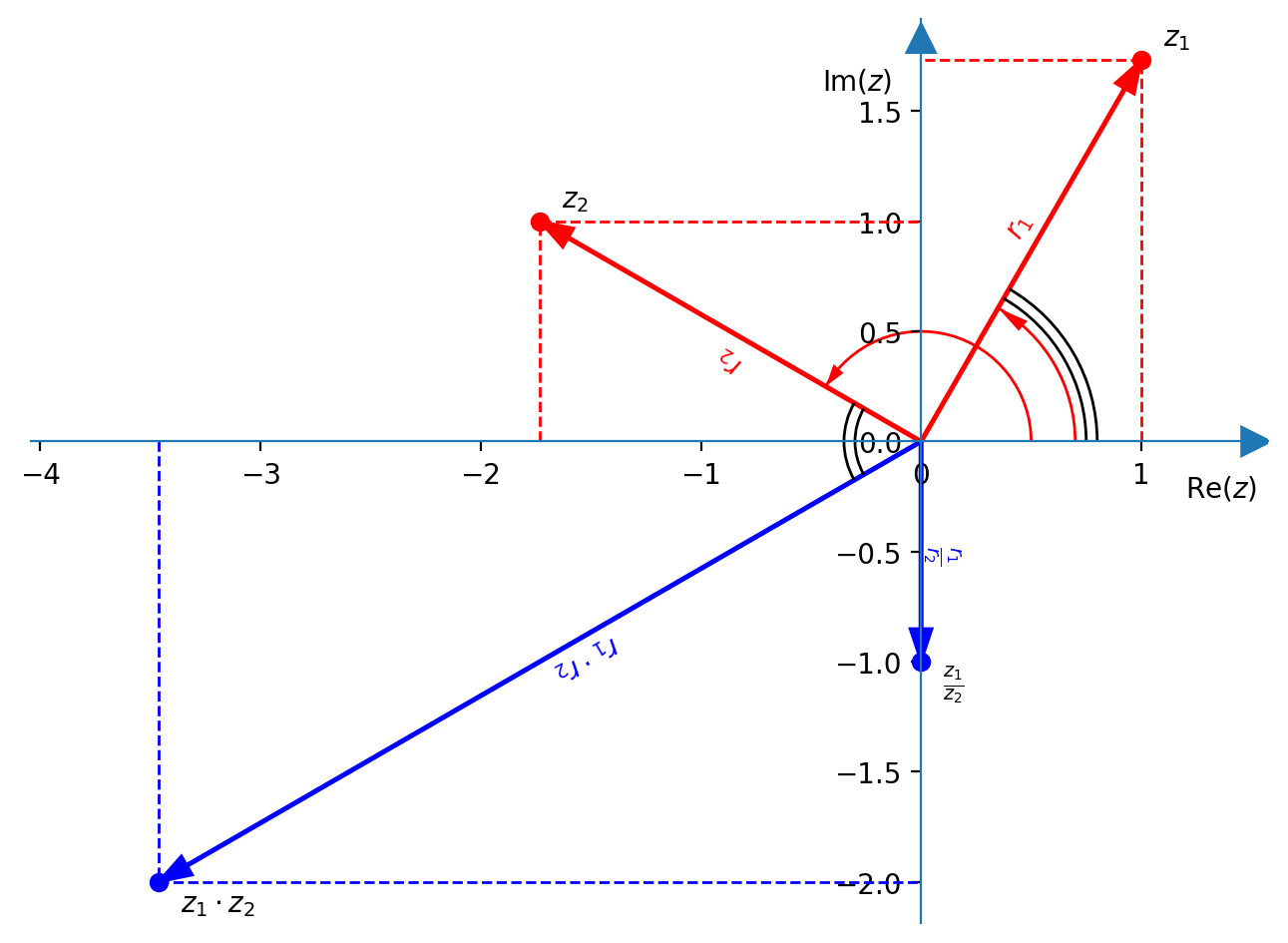
Per la rappresentazione grafica scriviamo i numeri in forma algebrica cioè
- $z_1 = 1+\sqrt{3}i\;=\; 2\operatorname{cis}{\left({\pi\over 3}\right)}$
- $z_2 = -\sqrt{3}+i \;=\; 2\operatorname{cis}{\left({5\over6}\pi\right)}$
- $z_1 \cdot z_2 \;=\; -2\sqrt{3} -2i \;=\; 4 \operatorname{cis}{\left(-{5\over6}\pi\right)} \;=\; 4 \operatorname{cis}{\left(-150^{\circ}\right)}$
- ${z_1 \over z_2} \;=\; -i \;=\; \operatorname{cis}{\left(-{\pi\over2}\right)} \;=\; \operatorname{cis}{\left(-90^{\circ}\right)}$
Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).
