Esercizi parte 1 sui numeri complessi 2/2

Indice degli esercizi (corso Analisi Matematica 1)

1. Scrivere in forma cartesiana il seguente numero complesso $z = \sqrt{2}\left({2-2i\over \left|1-i\right|}\right)-i$
2. Trovare $z$ tale che $(1-i) z + 2\overline{z} = 2i$
3. Se $\left|z\right|=1$ allora dimostrare che
   • $(z-1)(\overline{z}+1)$ è un numero immaginario puro
   • $(z^2+1)\overline{z}$ è un numero reale puro
4. Calcolare $i^{35^3}$
5. Dimostrare che l'area del triangolo di vertici $0$, $z$, $w$ è ${1\over2} \left|\operatorname{Im}\left(\overline{z}w \right)\right|$

Soluzione

Esercizio 1

Scrivere in forma cartesiana il seguente numero

$$z = \sqrt{2}\left({2-2i\over \left|1-i\right|}\right)-i$$

Soluzione

Si ha $$ \begin{aligned} z &= \sqrt{2}\left({2-2i\over \left|1-i\right|}\right)-i \;=\; 2\sqrt{2} {1-i\over \sqrt{1+1}}-i \\ &= 2\cancel{\sqrt{2}} {1-i\over \cancel{\sqrt{2}}}-i \;=\; 2(1-i)-i \\ &= 2-3i \end{aligned} $$

Esercizio 2

Trovare $z$ tale che

$$(1-i) z + 2\overline{z} = 2i$$

Soluzione

Posto $z=a+bi$, e sviluppando l'equazione, si ha $$ \begin{gathered} (1-i) z + 2\overline{z} = 2i\\ (1-i) (a+bi) +2\overline{(a+bi)} = 2i \\ (1-i)(a+bi) +2(a-bi) = 2i \\ a + bi - ai + b + 2a - 2bi = 2i\\ (a + b +2a) + (b-a-2b)i = 2i \end{gathered} $$

Uguagliando parte reale e immaginaria si ottiene $$ \begin{cases} b+3a = 0 \\ -b-a = 2 \end{cases} \;\implies\; \begin{cases} b= -3a \\ +3a -a = 2 \end{cases} \;\implies\; \begin{cases} b = -3 \\ a = 1 \end{cases} \;\implies\; z = 1-3i $$

Esercizio 3

Se $\left|z\right|=1$ allora dimostrare che

• $(z-1)(\overline{z}+1)$ è un numero immaginario puro

• $(z^2+1)\overline{z}$ è un numero reale puro

Soluzione

Se $\left|z\right|=1$ allora la prima espressione diventa $$ (z-1)(\overline{z}+1) = z\overline{z} + z - \overline{z} -1 = \cancel{1} + z - \overline{z} -\cancel{1} = 2\operatorname{Im}\left(z\right)i $$

Essendo $\operatorname{Im}(z)$ un numero reale, allora $2\operatorname{Im}\left(z\right)i$ è immaginario puro

Esercizio 3

Se $\left|z\right|=1$ allora la seconda espressione diventa $$ (z^2+1)\overline{z} = z\cdot \overbrace{\cancel{(z\overline{z})}}^{1} + \overline{z} = z + \overline{z} = 2\operatorname{Re}\left(z\right) $$

Essendo $\operatorname{Re}\left(z\right)$ un numero reale, allora $2\operatorname{Re}\left(z\right)$ è reale puro

Esercizio 4

Calcolare $$i^{35^3}$$

Soluzione

Osserviamo che

da cui

Indichiamo con $k=35^3$, da cui $$ \begin{aligned} k &=35^3 = (32+3)^3 = 32^3 + 3 \cdot 32^2 \cdot 3 + 3 \cdot 32 \cdot 3^2 + 3^3 \\ &= 4 m + 27 = 4 m + 24 + 3 = 4 n + 3 \quad\text{per un certo}\quad n\in\mathbb{N} \end{aligned} $$

Quindi, si ha $$i^{35^3} = i^{4n+3} = -i$$

Esercizio 5

Dimostrare che l'area del triangolo di vertici $0$, $z$, $w$ è

$${1\over2} \left|\operatorname{Im}\left(\overline{z}w \right)\right|$$

Soluzione

I punti $O=(0,0)$, $z=(x_z,y_z)$ e $w=(x_w,y_w)$ rappresentano i vertici di un triangolo, la cui area ${1\over2} \left|\operatorname{Im}\left(\overline{z}w \right)\right|$ è $$ \begin{aligned} {1\over2} \left|\operatorname{Im}\left(\overline{z}w \right)\right| &= {1\over2} \left| \operatorname{Im}\left((x_z - y_z i) \cdot (x_w + y_w i)\right)\right| \\ &= {1\over2} \left| \operatorname{Im}\left((x_z x_w + y_z y_w) + (x_z y_w - y_z x_w)i\right) \right|\\ &= {1\over2} \left| x_z y_w - y_z x_w\right| \end{aligned} $$

Forniamo una soluzione geometrica ed una vettoriale

Per la soluzione geometrica osserviamo la figura, dove

"Area con sengno" = "Area triangolo" - "Area triangolo 1" - "Area trapezio"

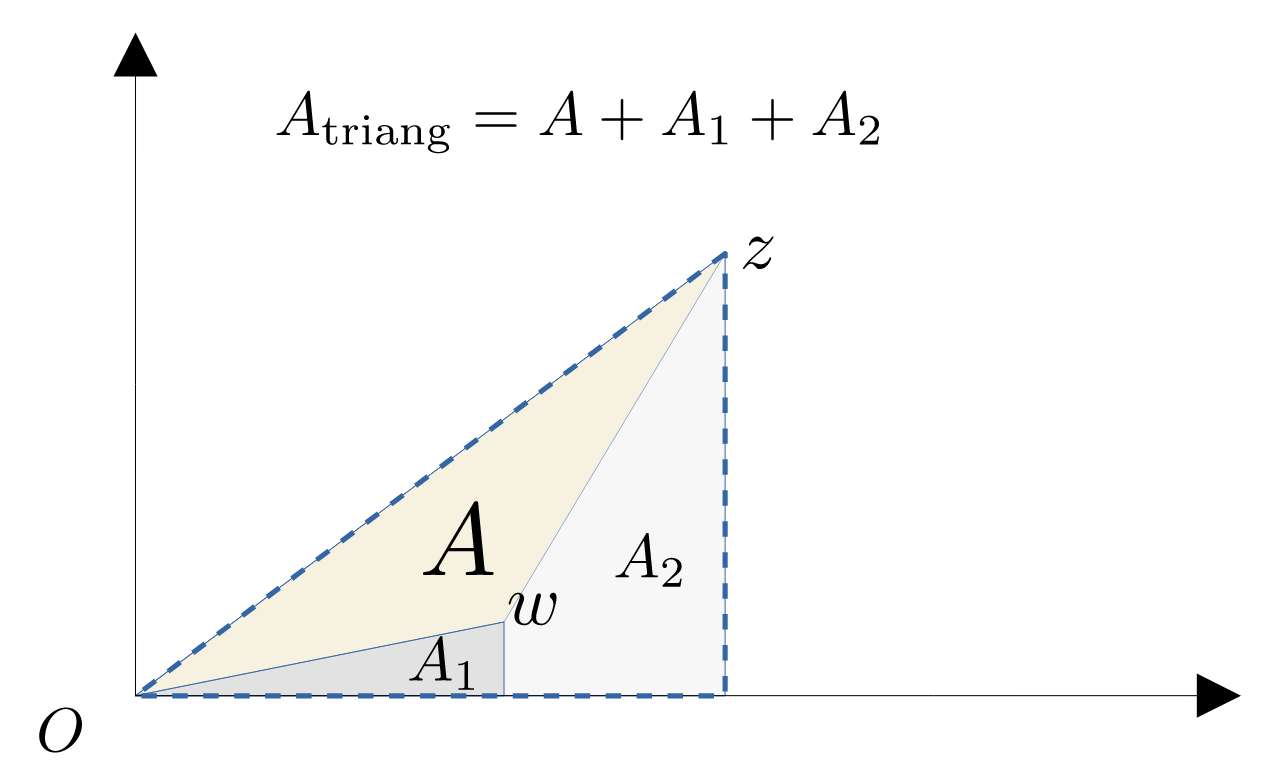
Quindi, si ha $$ \begin{aligned} A_{\operatorname{sign}} &= {1\over2} x_z y_z - {1\over2}x_w y_w - \left({(y_w+y_z)\cdot(x_z-x_w) \over 2}\right) \\ &= \cancel{{1\over2} x_z y_z} - \cancel{{1\over2}x_w y_w} - {1\over2} y_w x_z - \cancel{{1\over2} x_z y_z} + \cancel{{1\over2}x_w y_w} + {1\over2} y_z x_w \\ &= - {1\over2} y_w x_z + {1\over2} y_z x_w \\ &= {1\over 2} (y_z x_w - x_z y_w) \end{aligned} $$

Per la soluzione vettoriale osserviamo la figura.

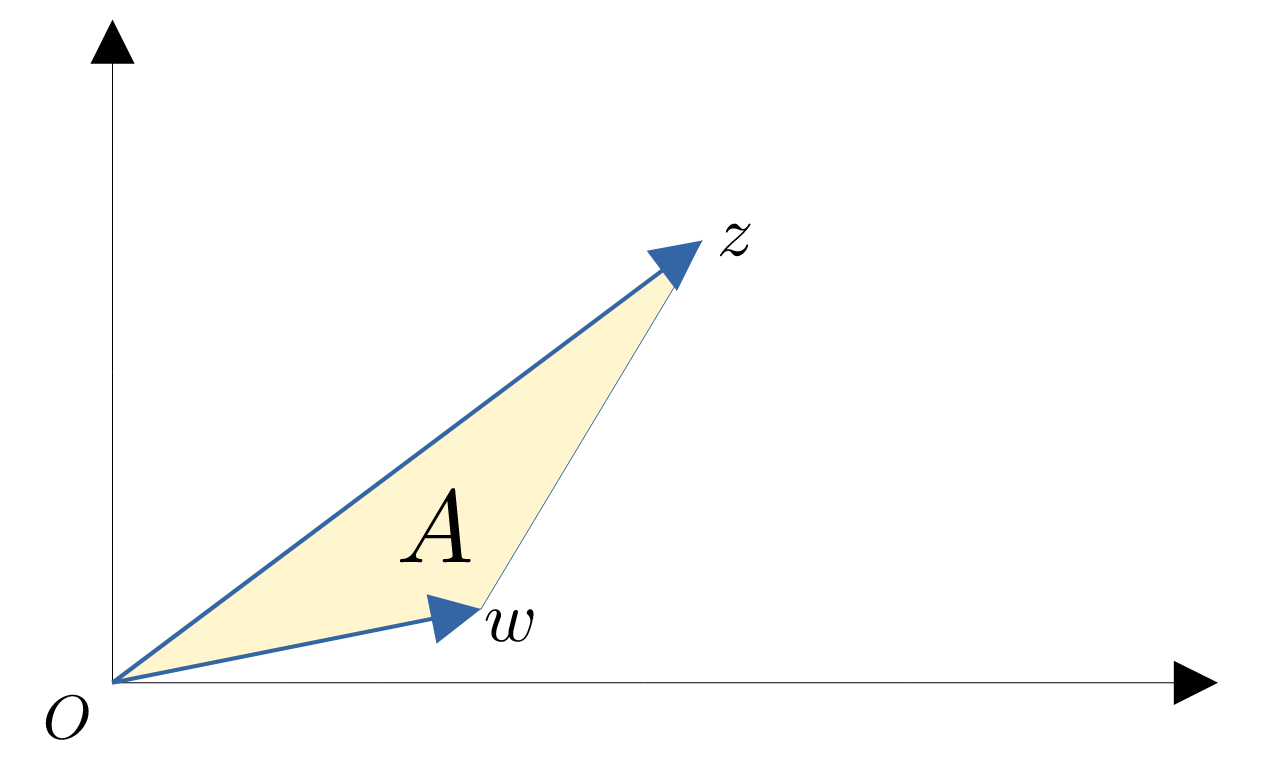
I punti $O=(0,0)$, $z=(x_z,y_z)$ e $w=(x_w,y_w)$ rappresentano i vertici di un triangolo, la cui area è $$ S = {1\over2} \left| \begin{array}{cc} x_z-0 & y_z-0\\ x_w-0 & y_w-0\\ \end{array} \right| = {1\over2} \left|x_z y_w - y_z x_w\right| $$

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).