L'esponenziale
Obiettivo (corso Analisi Matematica 1)
- Ripasso sull'esponenziale
- Proprietà dell'esponenziale a seconda della base $0 < a < 1$ o $a>1$
- Equazioni e disequazioni con l'esponenziale
- Esempi
L'esponenziale
La funzione esponenziale ha la forma $$ y = a^x $$ con $a>0$, fissato detto base e $x\in\mathbb{R}$
Esempio di grafico
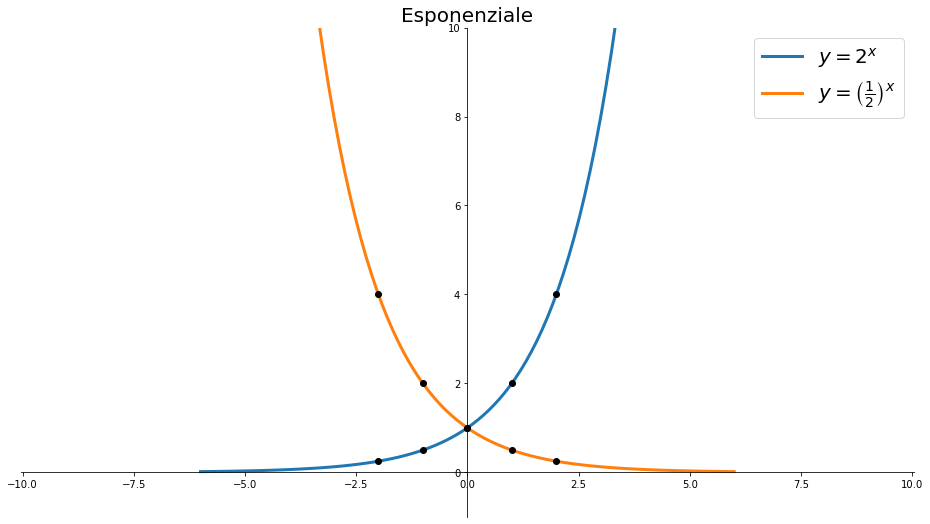
Disegnare il grafico dell'esponenziale per $a=2$ e $a={1\over2}$
Soluzione
Per ottenere il grafico di $y_1=2^{x}$ e $y_2=\left({1\over 2}\right)^{x}$ costruiamo la tabella di valutazione
| $x$ | $y_1=2^{x}$ | $y_2=\left({1\over 2}\right)^{x}$ |
|---|---|---|
| -2 | $2^{-2}={1\over 2^2}={1\over4}$ | $\left({1\over 2}\right)^{-2}=2^2=4$ |
| -1 | $2^{-1}={1\over 2^1}={1\over2}$ | $\left({1\over 2}\right)^{-1}=2^1=2$ |
| 0 | $2^0=1$ | $\left({1\over 2}\right)^{0}=1$ |
| 1 | $2^1=2$ | $\left({1\over 2}\right)^{1}={1\over2}$ |
| 2 | $2^2=4$ | $\left({1\over 2}\right)^{2}={1\over2^2}={1\over4}$ |
Per $x$ positivo molto grande
- $2^{x}$ diventa numero molto grande
- $\left({1\over 2}\right)^{x}={1\over 2^x}$ è la divisione di $1$ per un numero positivo molto grande e quindi il risultato è un numero positivo molto piccolo vicino allo zero
Per $x$ negativo molto grande
- $2^{x}={1\over 2^{-x}}$ diventa un numero molto piccolo perché $-x$ diventa positivo molto grande
- $\left({1\over 2}\right)^{x}=2^{-x}$ diventa un numero molto grande perché $-x$ diventa positivo molto grande
L'esponenziale: proprietà
Ci sono tre casi notevoli di $a^{x}$ da discutere:
- per $a>1$ la funzione è crescente, i.e. $x>y\implies a^x>a^y$
- per $0 < a < 1$ la funzione è decrescente, i.e. $x>y\implies a^x<a^y$ !!!
- per $a=1$ la funzione è costante, i.e. $y=1$
Inoltre, l'esponenziale ha
- il dominio, ovvero tutti i valori che può assumere la $x$: $\mathbb{R}$
- il codominio, ovvero tutti i valori assunti dalla $y$: $\mathbb{R}^{+}$
(tutti i numeri reali positivi con esclusione dello zero)
L'esponenziale: proprietà
Le funzioni esponenziali hanno le stesse proprietà delle potenze, ovvero
- $a^x\cdot a^y=a^{x+y}$
- $\frac{a^x}{a^y}=a^{x-y}$
- $(a\cdot b)^x=a^{x}\cdot b^y$
- $(a^x)^y=a^{xy}$
- $a^{-x}={1\over a^{x}}=\left({1\over a}\right)^x$
Esempi
Esempio 1
Risolvere l'equazione
$$3^{x+1}-{1\over 3^x}=2$$
Soluzione
Ponendo $t=3^x$ si ha $$ 3t-{1\over t}=2 \;\implies\;{3t^2-2t-1\over t}=0 $$
Essendo $t\ne0$, anzi $t\geqslant0$ si ha $$ 3t^2-2t-1 = 0\;\implies\;t_{1,2}={+2\pm\sqrt{4+12}\over 6}={+2\pm4\over 6}=\left\{1,\;-{1\over3}\right\} $$
Quindi le soluzione sono
- $t=1\implies 3^x=1\implies 3^x=3^0\implies x=0$
- $t=-{1\over3}\implies 3^x=-{1\over3}\implies x=\left\{\emptyset\right\}$
Esempio 2
Risolvere le disequazioni
$$3^{x} \geqslant 0,\ \quad 3^{x} \geqslant 1,\ \quad 3^{x} \geqslant 3,\ \quad 3^{x} \geqslant {1\over 3}$$
Sappiamo che l'esponenziale è sempre positivo, quindi
$$3^{x} \geqslant 0 \;\implies\; x\in\mathbb{R}$$
Dalle proprietà delle potenze si ha
$$ 1 =3^{0} $$
e quindi (funz. crescente)
$$3^{x} \geqslant 3^{0} \;\implies\; \left\{x\geqslant 0\right\}$$
Dalle proprietà delle potenze si ha
$$3 = 3^{1}$$
e quindi (funz. crescente)
$$ 3^{x} \geqslant 3^{1} \;\implies\; \left\{x\geqslant 1\right\} $$
Dalle proprietà delle potenze si ha
$${1\over 3} =3^{-1}$$
e quindi (funz. crescente)
$$3^{x} \geqslant 3^{-1} \;\implies\; \left\{x\geqslant -1\right\}$$
Esempio 3
Risolvere le disequazioni
$$\left({1\over 3}\right)^{x} \geqslant 0,\ \quad \left({1\over 3}\right)^{x} \geqslant 1,\ \quad \left({1\over 3}\right)^{x} \geqslant 3,\ \quad \left({1\over 3}\right)^{x} \geqslant {1\over 3}$$
Nota:
Si potrebbe convertire
$$ \left({1\over 3}\right)^{x} \;=\; 3^{(-x)} $$
(lascio a voi di provare questa strada simile all'esercizio 2, ma fate attenzione al segno meno)
Sappiamo che l'esponenziale è sempre positivo, quindi
$$ \left({1\over 3}\right)^{x} \geqslant 0 \;\implies\; x\in\mathbb{R} $$
Dalle proprietà delle potenze si ha
$$ {1\over 3} = \left({1\over 3}\right)^{0} $$
e quindi (funz. decrescente)
$$ \left({1\over 3}\right)^{x} \geqslant \left({1\over 3}\right)^{0} \;\implies\; \left\{x\leqslant 0\right\} $$
Dalle proprietà delle potenze si ha
$$ 3 = \left({1\over 3}\right)^{-1} $$
e quindi (funz. decrescente)
$$ \left({1\over 3}\right)^{x} \geqslant \left({1\over 3}\right)^{-1} \;\implies\; \left\{x\leqslant -1\right\} $$
Dalle proprietà delle potenze si ha
$$ {1\over 3} = \left({1\over 3}\right)^{1} $$
e quindi (funz. decrescente)
$$ \left({1\over 3}\right)^{x} \geqslant \left({1\over 3}\right)^{1} \;\implies\; \left\{x\leqslant 1\right\} $$
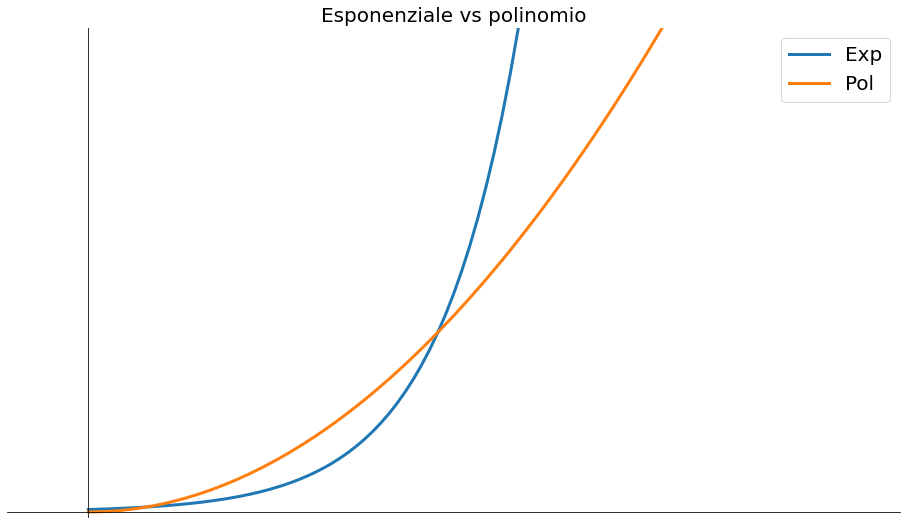
Curiosità: crescita esponenziale vs crescita polinomiale
Per $x$ grandi vince sempre l'esponenziale
Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).
