Elementi di geometria

Obiettivo (corso Analisi Matematica 1)

Ripasso sul Piano cartesiano
Retta / Retta per due punti
Fascio di rette
Esempi

VIDEO

PDF

Piano cartesiano

Punto $P=(x,y)$ del piano dove

$x$ posizione lungo l'asse "x" detto delle ascisse
$y$ posizione lungo l'asse "y" detto delle ordinate

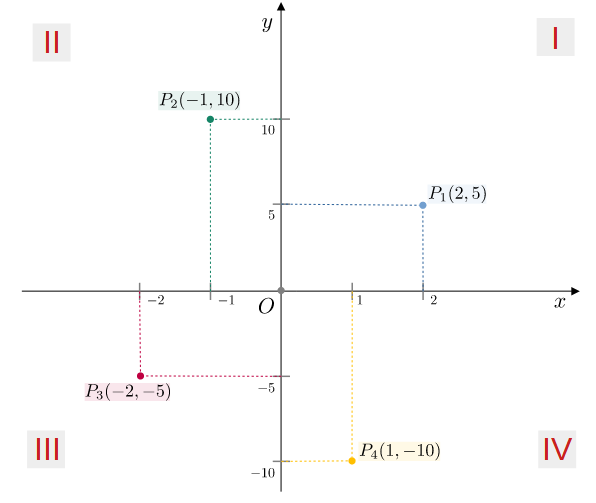
I punti nel

I quadrante: $x$ e $y$ positiva
II quadrante: $x$ negativa e $y$ positiva
III quadrante: $x$ e $y$ negativa
IV quadrante: $x$ positiva e $y$ negativa

Piano cartesiano: distanza

Distanza tra due punti $P_1(x_1,y_1)$ e $P_2(x_2,y_2)$ è data dal teorema di Pitagora: $$ d = \sqrt{\left(x_2-x_1\right)^2+\left(y_2-y_1\right)^2} $$

Ad esempio, la distanza di $P_1$ dall'origine $O$ è $$d_{P_1,O} = \sqrt{\left(2-0\right)^2+\left(5-0\right)^2})=\sqrt{4+25}=\sqrt{29}$$

Esercizio 1

Rappresentare graficamente i seguenti punti

$$P_1(-1,-1)\;,\; P_2(1,-1)\;,\; P_3(1,1)$$

e calcolare le relative distanze

Soluzione

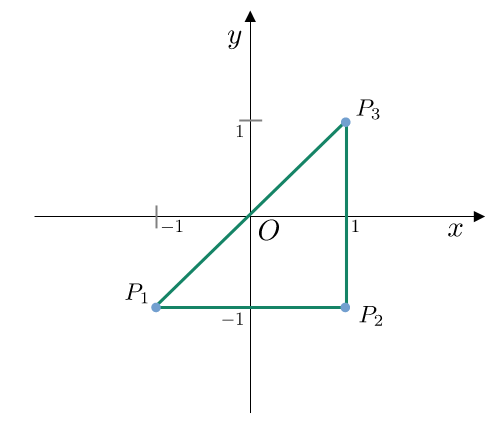
Le distanze sono:

$d_{P_1,P_2} \;=\; \sqrt{\left(-1-1\right)^2+\left(-1+1\right)^2}) \;=\; \sqrt{4+0} \;=\; 2$
$d_{P_1,P_3} \;=\; \sqrt{\left(-1-1\right)^2+\left(-1-1\right)^2}) \;=\; \sqrt{4+4} \;=\; \sqrt{8} \;=\; 2\sqrt{2}$
$d_{P_2,P_3} \;=\; \sqrt{\left(1-1\right)^2+\left(-1-1\right)^2}) \;=\; \sqrt{0+4} \;=\; 2$

Retta: equazione

L'equazione della retta è la seguente: $$y=mx+q$$ dove $m$ è detto coefficiente angolare e $q$ termine noto

Si ha

se $m>0$ la retta è crescente
se $m<0$ la retta è decrescente
se $q=0$ la retta passa per l'origine

Retta: disegno

Per il disegno della retta servono due punti

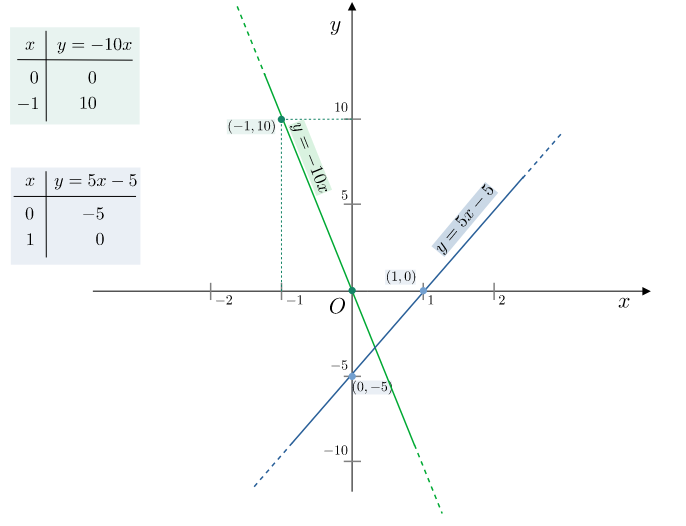
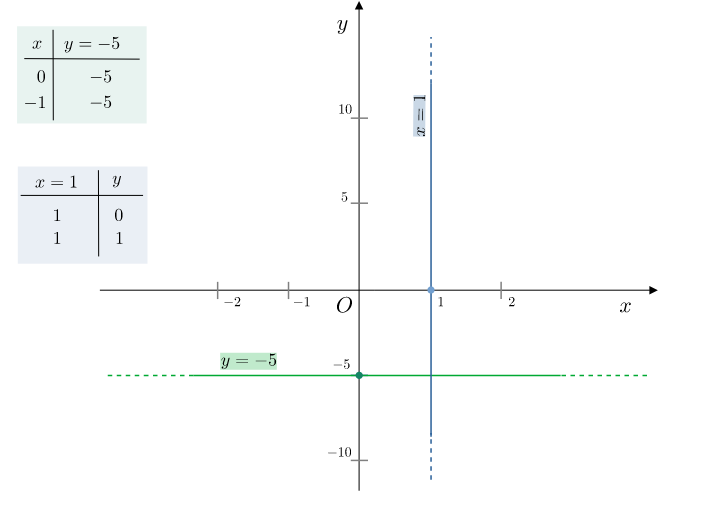
Retta orizzontale e verticale

Retta orizzontale: $y=c$ con $c$ costante

Retta verticale: $x=c$ con $c$ costante

Esercizio 2

Rappresentare graficamente le seguenti rette

$y=2x+1$

$y=-{1\over 2}x-1$

e trovare il punto di intersezione.

Nota: Il punto di intersezione è quel valore di $x$ e $y$ per cui le due equazioni sono uguali, i.e. va risolto il sistema

Soluzione

Per disegnare la prima retta di equazione $y=2x+1$ la valutiamo nei punti

per $x=0$ si ha $y=1$
per $x=1$ si ha $y=3$

Per disegnare la prima retta di equazione $y=-{1\over 2}x-1$ la valutiamo nei punti

per $x=0$ si ha $y=-1$
per $x=2$ si ha $y=-2$

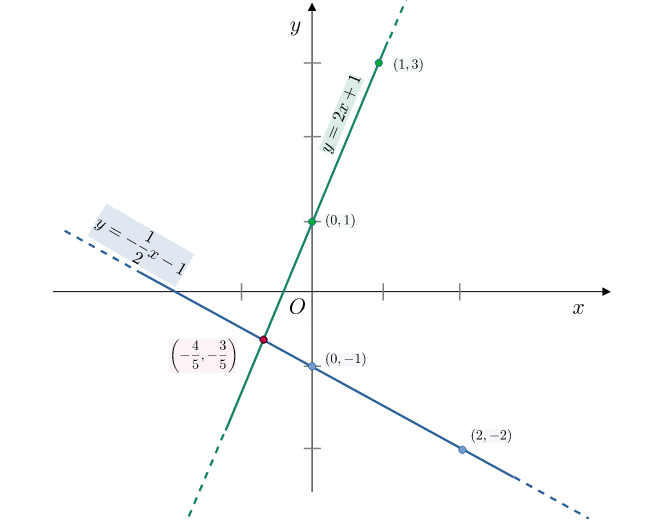
Il punto di intersezione si ottiene risolvendo il sistema $$\begin{cases} y=2x+1\\ y=-{1\over 2}x-1 \end{cases}$$

Sostituendo la prima equazione nella seconda si ha $$ 2x+1 = -{1\over 2}x-1 \;\implies\;\left(2+{1\over 2}\right)x=-2 \;\implies\;x=-{4\over5} $$ e, sostituendo $x=-{4\over5}$ nella prima equazione, si ha $$ y = 2\left(-{4\over5}\right)+1={-8+5\over5}=-{3\over5} $$

Retta per due punti

Dati due punti $P1(x_1,y_1)$ e $P1(x_2,y_2)$ la retta passante per questi due punti è

$$ {\frac {y-y_{1}}{y_{2}-y_{1}}}={\frac {x-x_{1}}{x_{2}-x_{1}}} $$

In forma implicita è:

$$ (x_{2}-x_{1})\cdot (y-y_{1})-(y_{2}-y_{1})\cdot (x-x_{1})=0 $$

Nota: La forma implicita contempla la retta verticale quella esplicta no!

Fascio di rette

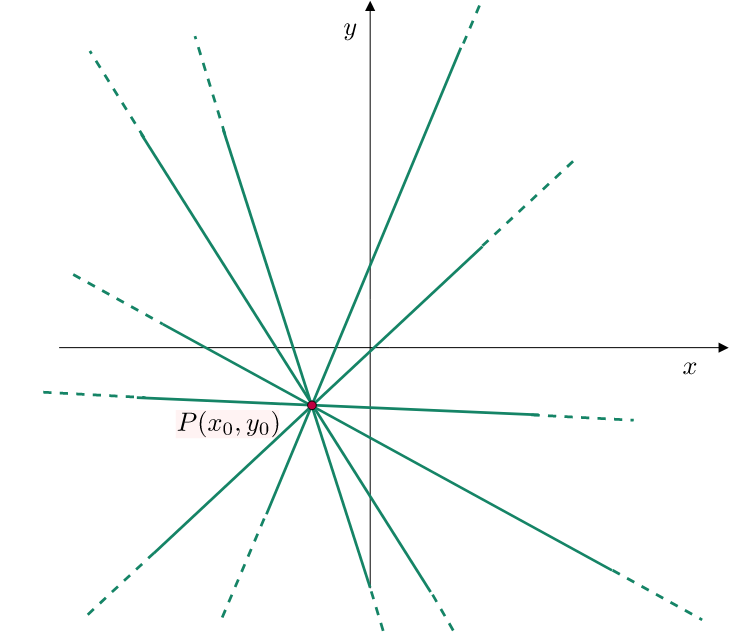
Il fascio proprio di rette (tranne la retta verticale) sono tutte le rette passanti per $P(x_{0},y_{0})$ ed ha equazione

$$ y-y_{0}=m(x-x_{0}) $$

Il piano cartesiano: origine

Nicola d'Oresme, 1300
René Descartes (in italiano Renato Cartesio), 1600
Pierre de Fermat (non pubblicò mai la sua scoperta)

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).