Rappresentazione grafica e ordinamento nei complessi
Obiettivo (corso Analisi Matematica 1)
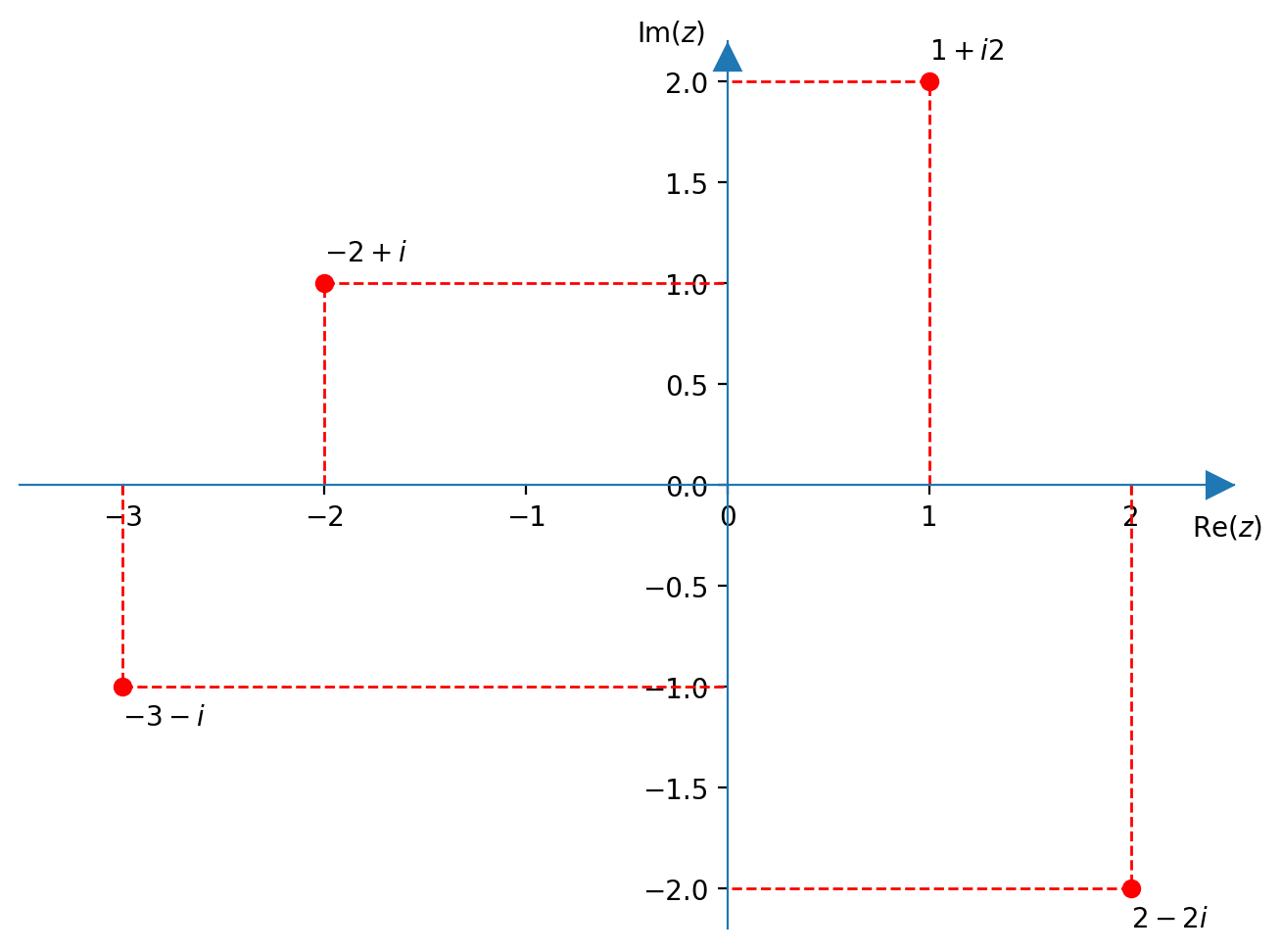
Rappresentazione grafica nel piano complesso (o piano di Gauss)
Un numero complesso $z=a+bi$ viene rappresentato in un piano cartesiano come un punto $(a,b)$
- asse $x$: parte reale
- asse $y$: parte immaginaria
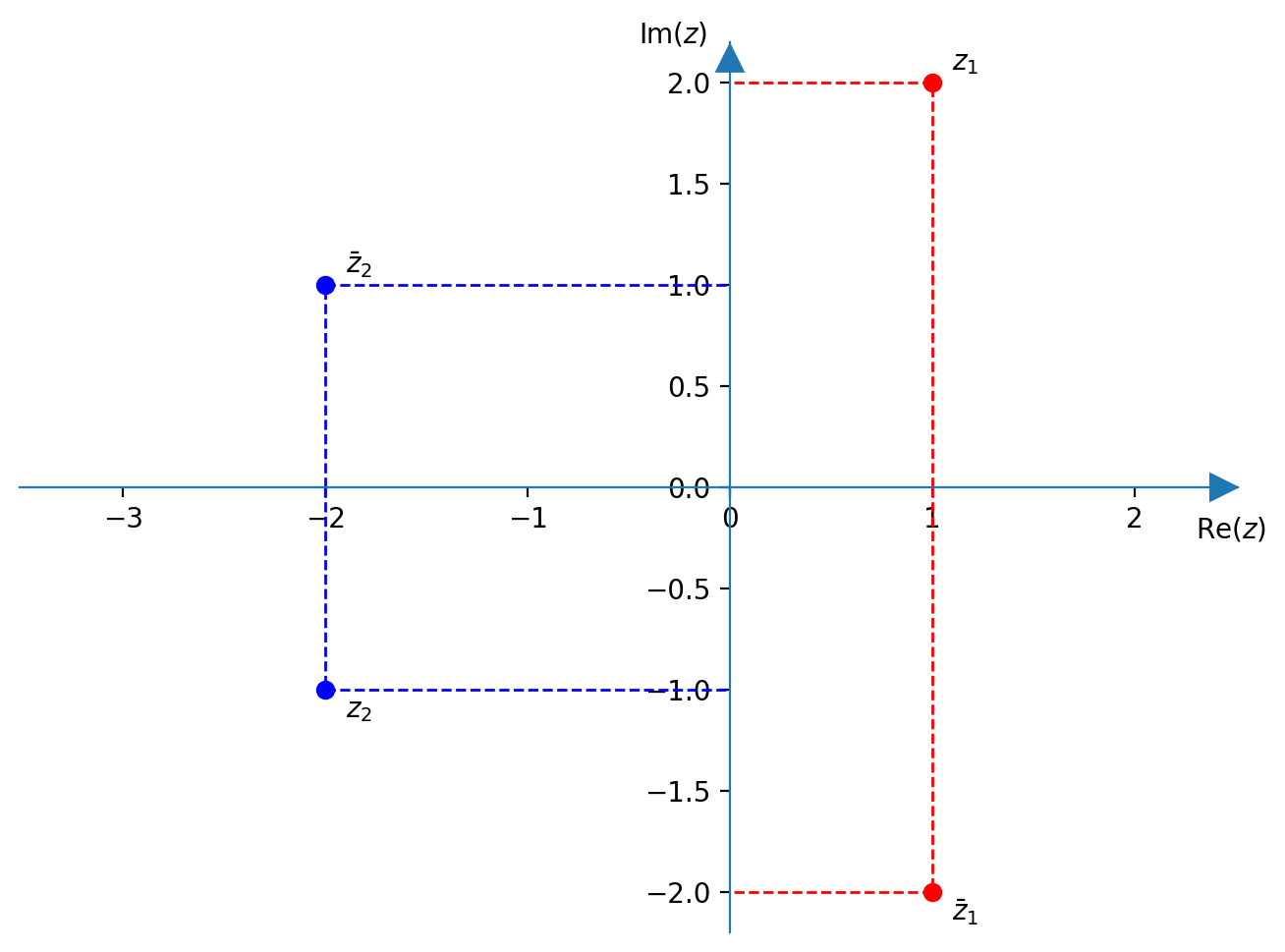
Coniugato
Dato il numero complesso $z=a + bi$ il suo coniugato è $\overline{z} = a-bi$ $$ \begin{cases} \operatorname{Re}(z_1)=\operatorname{Re}(z_2) \\ \operatorname{Im}(z_1)=-\operatorname{Im}(z_2) \end{cases} \;\implies\; \text{simmetrico rispetto all'asse x} $$
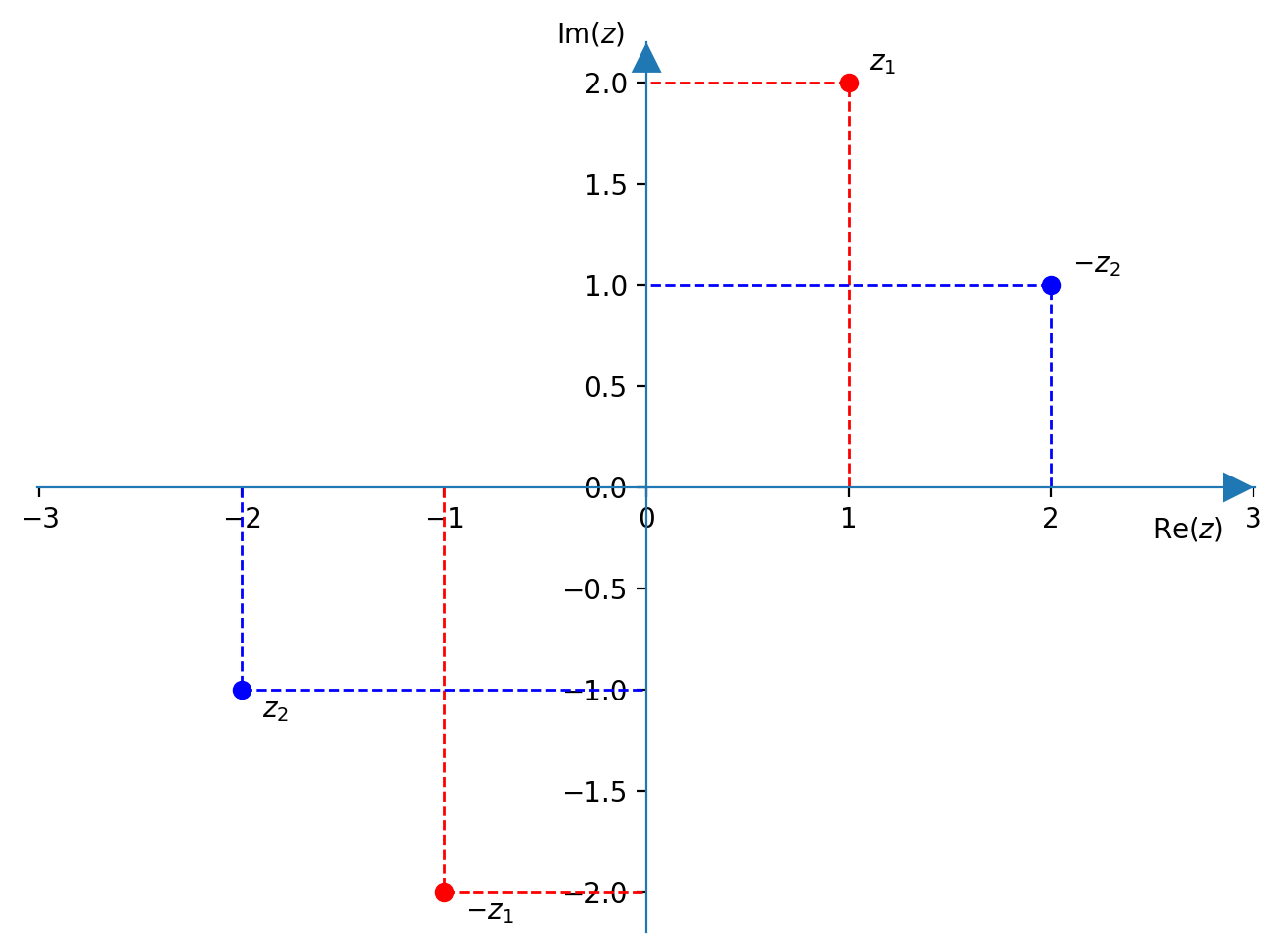
Opposto
Dato il numero complesso $z=a + bi$ il suo opposto è $-z = -a - bi$
E' il punto simmetrico di $z$ rispetto all'origine (parte reale e immaginaria opposte)
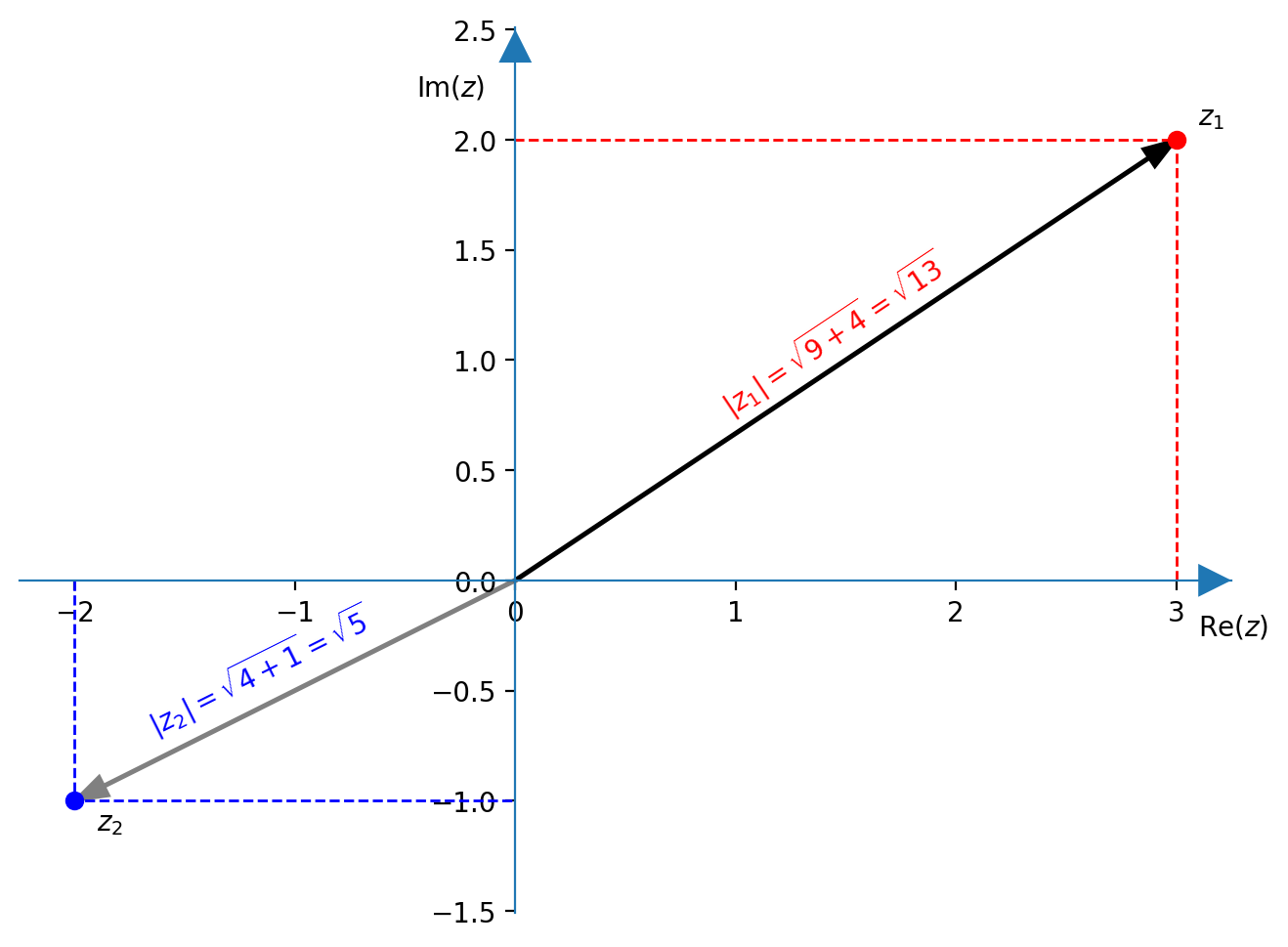
Modulo
Dato il numero complesso $z=a + bi$ il suo modulo è $\left|z\right|= \sqrt{a^2+b^2}$
Se il numero complesso $z$ viene interpretato come un vettore allora il suo modulo è la sua lunghezza
Somma
I numeri complessi (se interpretati come dei vettori) si sommano con la regola del parallelogramma
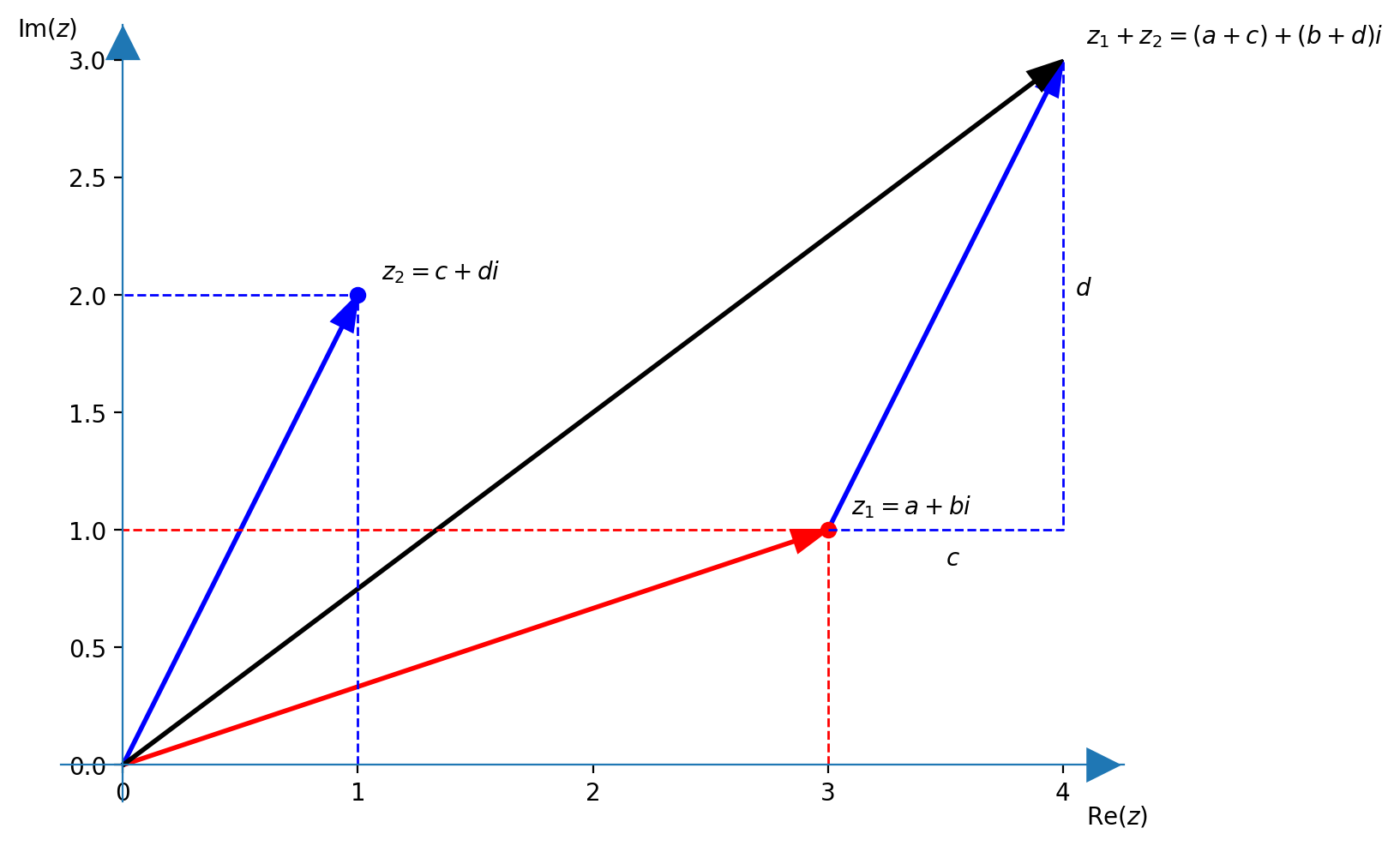
Si può dare un'interpretazione grafica della disuguaglianza triangolare $$ \left|z+w\right| \leqslant \left|z\right|+ \left|w\right| $$ come la lunghezza del vettore somma è minore della lunghezza dei due vettori
Differenza
I numeri complessi (se interpretati come dei vettori) si sommano con la regola del parallelogramma
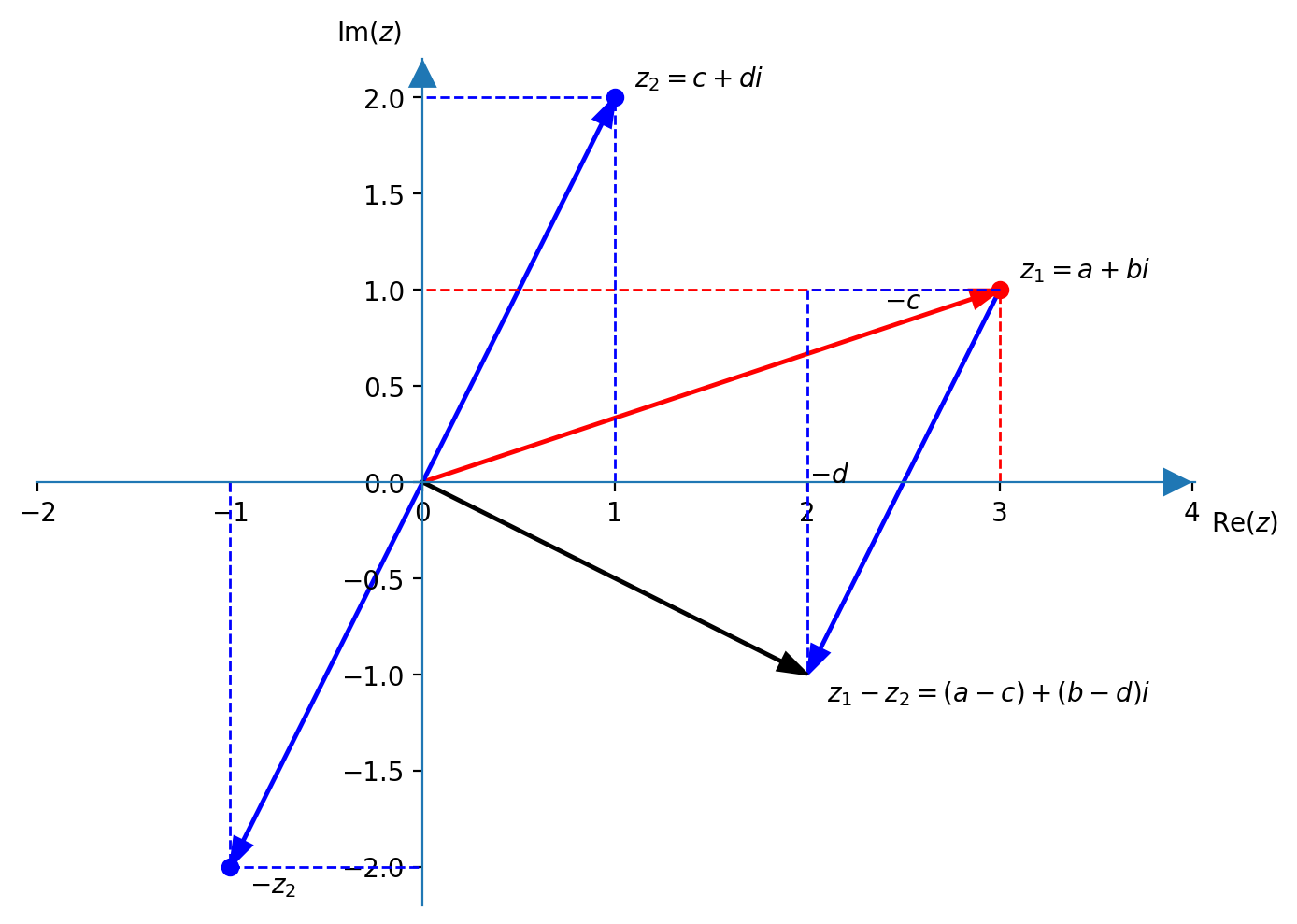
Ordinamento
Non è possibile definire una relazione $\le$ tra i numeri complessi
Dalle proprietà delle relazioni d'ordine (riflessiva, antisimmetrica e transitiva) segue che
- il quadrato di un numero è positivo
- l'opposto di un numero positivo è negativo
In $\mathbb{C}$, si ha $$ 1^2= 1 \quad\text{ e }\quad i^2= -1 $$ e quindi si hanno due quadrati (numeri positivi) che devono essere di segno opposto e questo è un assurdo
Quindi $\mathbb{C}$ non può essere un campo ordinato, i.e. non ha senso dare un ordine a $$ -1-2i < 1+2i \quad, \quad i < 2i \quad, \quad -1+2i < 1+2i \quad,\quad \ldots $$
Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).
