Il logaritmo
Obiettivo (corso Analisi Matematica 1)
- Ripasso sui logaritmi
- Il logaritmo viene introdotto come funzione inversa dell'esponenziale
- Equazioni e disequazioni con il logaritmo
- Esempi
Il logaritmo
Il logaritmo è l'operazione inversa dell'esponenziale, i.e. si deve trovare quel valore di $x$ tale che $$a^x=b\;\Longleftrightarrow x= \log_{a}b$$ e si legge "$x$ è uguale al logaritmo di $b$ (argomento) in base $a$"
L'equazione $a^x=b$ con $a>0$ e $a\ne1$ ha soluzione solo se $b>0$ (condizione di esistenza del logaritmo)
Se $a=e\approx2.71828\ldots$, dove $e$ è numero di Nepero, si parla di logaritmo naturale e si indica con il simbolo abbreviamo $\log(\cdot)$ oppure $\ln(\cdot)$
Funzioni inverse
- Logaritmo dell'esponenziale
$$ \log_a{a^{x}} = x $$
- Esponenziale del logaritmo
$$ a^{\log_a{x}} = x $$
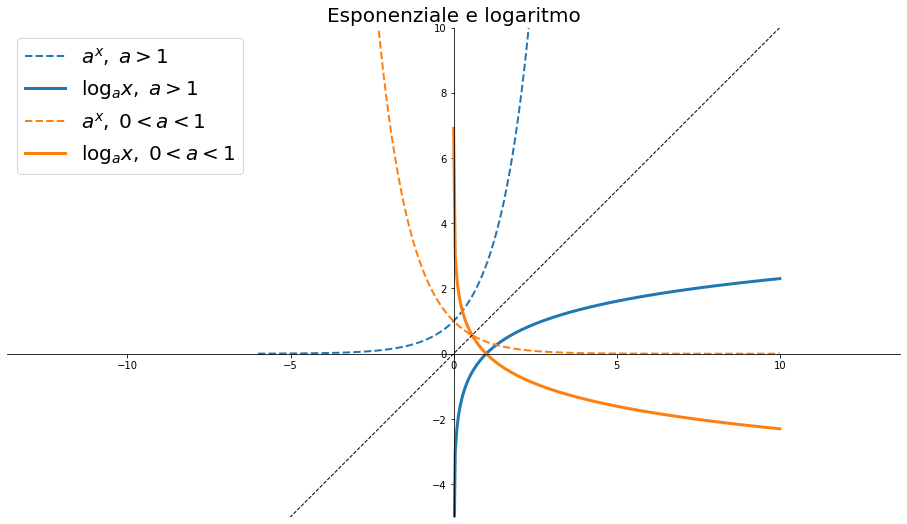
Il logaritmo: grafici
Se $(x_0,y_0)$ è un punto della funzione esponenziale, allora $(y_0,x_0)$ è un punto della funzione logaritmo.
Quindi i grafici delle funzioni logaritmiche si ottengono per simmetria rispetto alla bisettrice del I e III quadrante (proprietà delle funzioni inverse)
Il logaritmo: grafici
Il logaritmo: proprietà
Le proprietà dei logaritmo (con $a>0$ e $a\ne1$) sono le seguenti:
- $\log_{a}(x\cdot y)=\log_{a}x+\log_{a}y$ dove è richiesto $x,y>0$
- $\log_{a}\left({x\over y}\right)=\log_{a}x-\log_{a}y$ dove è richiesto $x,y>0$
- $\log_{a}x^y=y \cdot \log_{a}x$ dove è richiesto $x>0$
- $\log_{a}b={\log_{c}b\over \log_{c}a}$ (formula del cambio di base)
L'ultima formula nel caso di un cambiamento di base verso i logaritmi naturali diventa (usatissima)
$$ \log_{a}b={\ln b\over \ln a} $$
Il logaritmo: disequazioni
La funzione logaritmo è una funzione del tipo $$ y = \log_{a}x $$ che è valida (ha soluzione) solo se $x>0$
Si ha
- per $a>1$ la funzione è crescente, i.e. $x>y\implies \log_{a}x>\log_{a}y$
- per $0 < a < 1$ la funzione è decrescente, i.e. $x>y\implies \log_{a}x<\log_{a}y$
Esempi
Esempio 1
Semplificare
$$x=\log_{1\over2}2^3$$
Soluzione
Usando le proprietà del logaritmo e osservando che $$ \log_{1\over2}2=\log_{1\over2} \left({1\over2}\right)^{-1}=-1\cdot\log_{1\over2} \left({1\over2}\right) = -1\cdot1= -1 $$ si ha $$ \log_{1\over2}2^3 = 3\cdot \log_{1\over2}2 = 3\cdot -1 = -3 $$
Esempio 2
Risolvere l'equazione
$$e^x+3e^{-x}=4$$
Soluzione
Ponendo $t=e^x$ l'equazione diventa $$ t+3{1\over t}=4 $$
Essendo $t\ne0$ si ha $$ t^2-4t+3=0\;\implies\;t_{1,2}={4\pm\sqrt{16-12}\over 2}=\left\{3,\ 1\right\} $$
Quindi
- per $t=3$ si ha $3=e^x\implies x=\ln{3}$
- per $t=1$ si ha $1=e^x\implies x=\ln{1}=0$
(Verifica)
- per $x=0$ si ha $e^{0}+3e^{0}=4\;\iff\; 4=4$
- per $t=\ln{3}$ si ha $e^{\ln{3}}+3e^{-\ln{3}}=4\;\iff\; 3 + 3\cdot {1\over 3}=4 \;\iff\; 4=4$
Esempio 3
Risolvere la seguente disequazione
$$\log_2{x}\leqslant 0$$
Soluzione
Possiamo scrivere
$$ 0 = \log_2{1} $$
e quindi si ha (funz. crescente)
$$ \log_2{x}\leqslant \log_2{1} \;\implies\; 0<x \leqslant 1 $$
Nota: Ricordarsi sempre del dominio!

Esempio 4
Risolvere la seguente disequazione
$$\log_{1\over2}{x}\leqslant 1$$
Soluzione
Possiamo scrivere
$$ 1 = \log_{1\over 2}{{1\over 2}} $$
e quindi si ha (funz. decrescente)
$$ \log_{1\over2}{x}\leqslant \log_{1\over 2}{{1\over 2}} \;\implies\; x\geqslant {1\over 2} $$
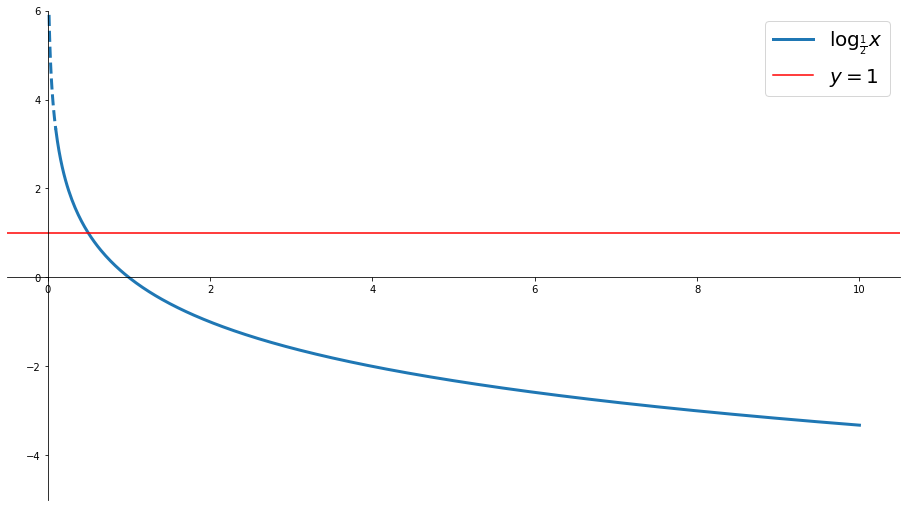
Esempio 5 (importantissimo)
Risolvere la seguente disequazione dove $a>0$
$$e^x\leqslant a\quad\text{ , }\quad e^x\geqslant a \quad\text{ , }\quad \ln{x}\leqslant a \quad\text{ , }\quad \ln{x}\geqslant a$$
Soluzione
La soluzione coinvolge le proprietà
$$ \log_a{a^{x}} = x \quad\text{ e }\quad a^{\log_a{x}} = x $$
Da $$a=e^{\ln a}$$ si ha $$e^x\leqslant e^{\ln a}\;\implies\; x \leqslant \ln a$$
Da $$a=e^{\ln a}$$ si ha $$e^x\geqslant e^{\ln a}\;\implies\; x \geqslant \ln a$$
Da $$a=\ln e^a$$ si ha $$\ln{x}\leqslant \ln e^a\;\implies\; 0 < x \leqslant e^a$$
Da $$a=\ln e^a$$ si ha $$\ln{x}\geqslant \ln e^a\;\implies\; x \geqslant e^a$$
Esempio 6
Trovare il dominio (o condizioni di esistenza) di
$$f(x)=\ln{\left({x\over x+1}\right)}$$
Soluzione
Il dominio di $f(x)=\ln{\left({x\over x+1}\right)}$ si ottiene imponendo l'argomento del logaritmo strettamente positivo, ovvero $$ {x\over x+1}>0 $$
Essendo una disequazione fratta, studiamo il segno della frazione
Il segno del numeratore e del denominatore sono:
- Numeratore: $x>0 \implies \left\{x>0\right\}$
- Denominatore: $x+1>0\implies \left\{x>-1\right\}$
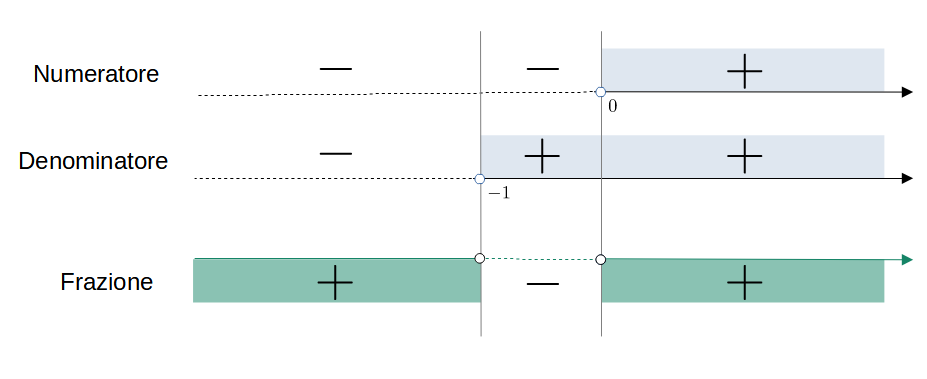
Quindi il rapporto tra numeratore e denominatore è positivo (rapporto tra due numeri positivi o negativi) per $$\left\{x<-1\right\}\;\lor\;\left\{x>0\right\}$$
Storia
- Il logaritmo fu proposto nel 1614 da Nepero
- Furono utilizzati in astronomia attraverso delle tavole di calcolo (la prima ad opera di Henry Briggs nel 1617)
- Solo nel 1730 ad opera di Eulero si ha definizione di esponenziale e logaritmo dove presenta il legame del logaritmo tramite la funzione inversa dell'esponenziale (approccio odierno)
- Il logaritmo nasce prima dell'esponenziale!
Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).
