L'equazione del cerchio, dell'ellisse e dell'iperbole
Obiettivo (corso Analisi Matematica 1)
- Ripasso sull'equazione del Ccerchio
- Ripasso sull'equazione del Ellisse
- Ripasso sull'equazione del Iperbole / Iperbole equilatera / Iperbole equilatera traslata (funzione omografica)
- Esempi
Il cerchio / circonferenza
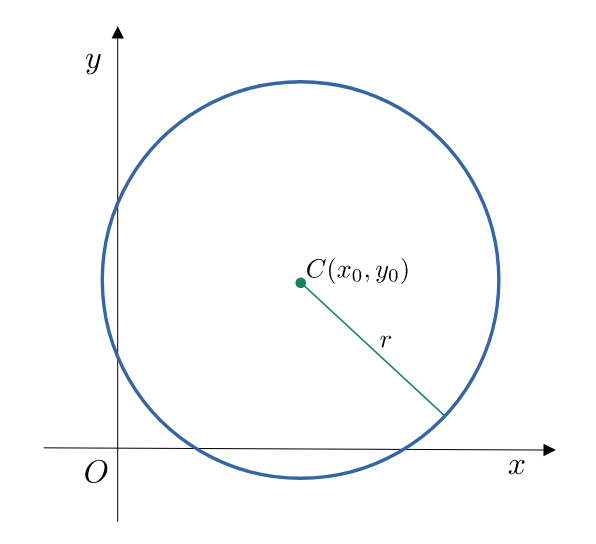
Il cerchio, di centro $C(x_0,y_0)$ e raggio $r>0$, ha equazione
$$ (x-x_0)^{2}+(y-y_0)^{2} = r^{2} $$
che può essere riscritto nella forma
$$ x^2 + y^2 + a x + by +c = 0 $$
dove
$$ a = -2x_0,\ b = -2y_0,\ c = x_0^2+y_0^2-r^2 $$
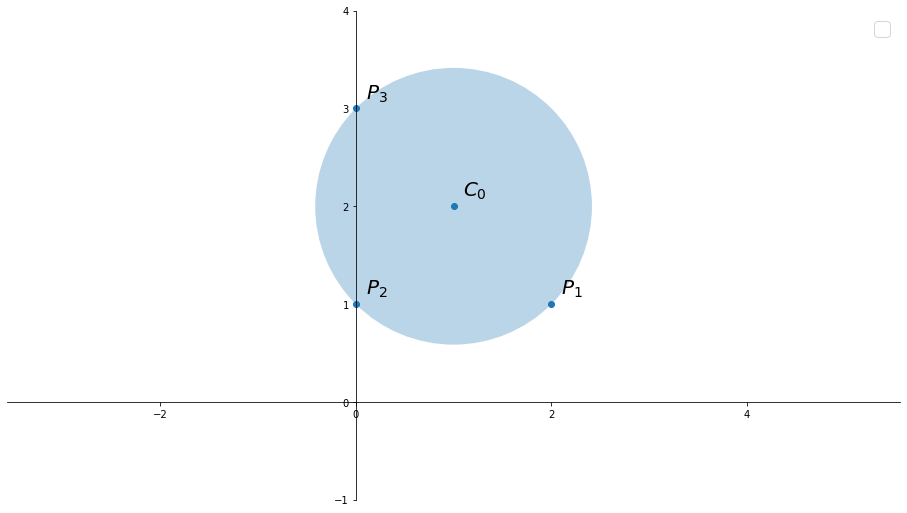
Esempio 1
Scrivere l'equazione della circonferenza passante per i punti $$P_1(2,\ 1),\; P_2(0,\ 1),\; P_3(0,\ 3)$$ e individuare il centro e il raggio
Soluzione
Dobbiamo scrivere le equazione di passaggio della circonferenza per 3 punti $$\begin{cases} 2^2 + 1^2 +a\cdot 2 + b\cdot 1 + c = 0\\ 0^2 + 1^2 +a\cdot 0 + b\cdot 1 + c = 0\\ 0^2 + 3^2 +a\cdot 0 + b\cdot 3 + c = 0\\ \end{cases} \;\implies\; \begin{cases} 2a + b + c = -5\\ b+c = -1\\ 3b + c = -9\\ \end{cases} \;\implies\; \begin{cases} a = -2\\ b = -4\\ c = 3\\ \end{cases}$$
Quindi
$$ x^2+y^2 -2x-4y+3 = 0 $$
Esplicitando il centro e il raggio si ha $$ (x-1)^2 + (y-2)^2 = (-3+1+4) \;\implies\; (x-1)^2 + (y-2)^2 = (\sqrt{2})^2 $$
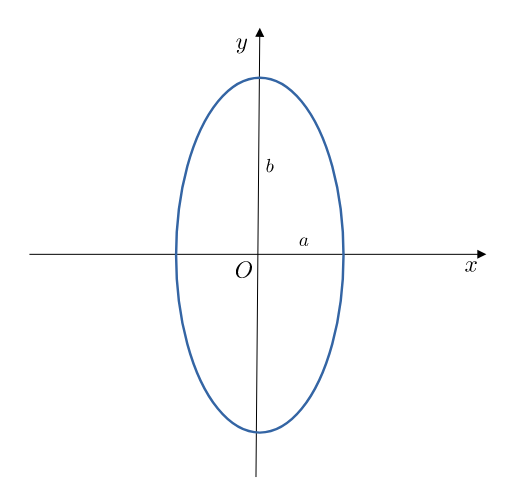
L'ellisse
L'ellisse centrata nell'origine ha equazione:
$$ \frac{x^{2}}{a^{2}}+\frac{y^{2}}{b^{2}}=1 $$
dove
- $2a$ asse lungo "x"
- $2b$ asse lungo "y"
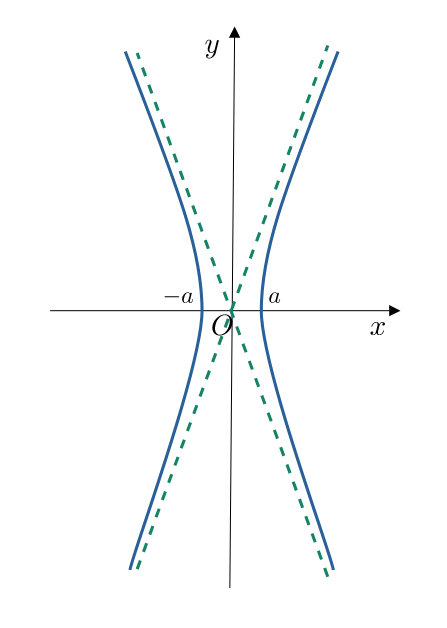
L'iperbole
L'iperbole centrata nell'origine con asse lungo "y" ha equazione:
$$ {\frac {x^{2}}{a^{2}}}-{\frac {y^{2}}{b^{2}}}=1 $$
Gli asintoti dell'iperbole hanno equazione $y=\pm {\frac {b}{a}}x$
Iperbole con asse lungo "x":
$$ {\frac {x^{2}}{a^{2}}}- {\frac {y^{2}}{b^{2}}}= -1 $$
Iperbole equilatera
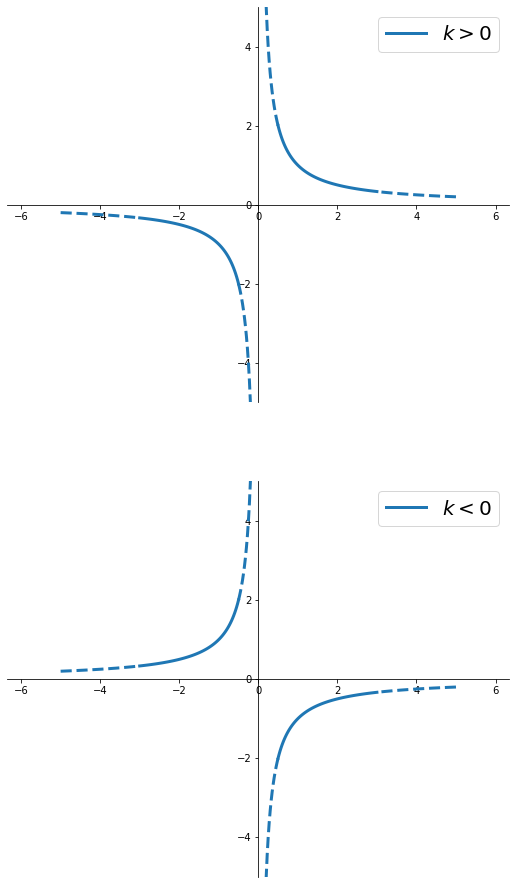
Se gli assi cartesiani coincidono con gli asintoti dell'iperbole abbiamo l'iperbole equilatera con centro in $(0,0)$ ed equazione
$$xy=k\;\iff\; y = {k\over x}$$
Iperbole equilatera traslata
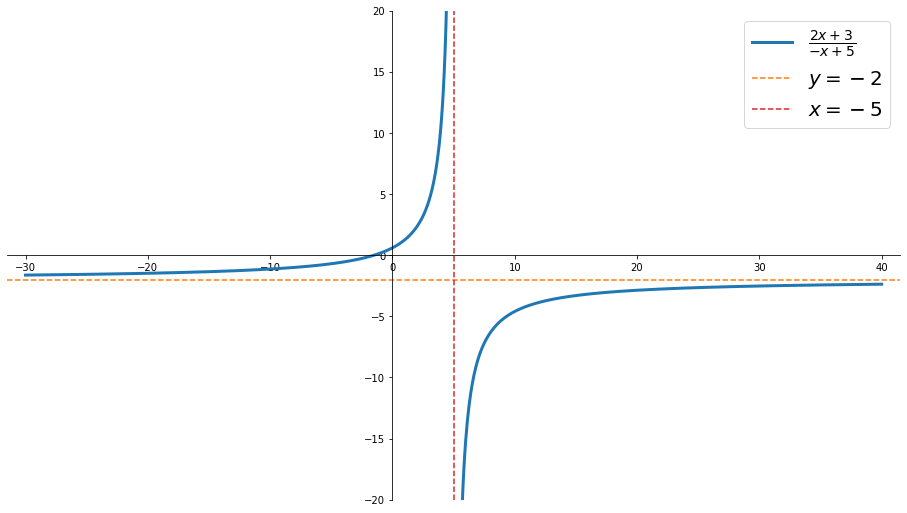
L'equazione dell'iperbole equilatera traslata (detta anche funzione omografica) è
$$ y\;=\;{\frac {ax+b}{cx+d}} $$
Proprietà:
- il centro è: $O\left(-{\frac {d}{c}};{\frac {a}{c}}\right)$
- asingoto orizzontale: $x=-{\frac {d}{c}}$
- asingoto verticale: $y=\frac {a}{c}$
Curiosità: Quanti punti di intersezione hanno due curve
Teorema (Bézout) Siano $\mathcal{C}$ e $\mathcal{D}$ due curve algebriche irriducibili e distinte di grado rispettivamente $m$ ed $n$. Allora l'intersezione di $\mathcal{C}$ e $\mathcal{D}$ ha al più $mn$ punti comuni.
Ad esempio, l'intersezione di una circonferenza (grado 2) con una parabola (grado 2) ha al più $2\times2=4$ punti di intersezione.

Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).
