La parabola
Obiettivo (corso Analisi Matematica 1)
- Ripasso sull'equazione della parabola
- Disegno della parabola (zeri / vertice / concavità)
- Esempi
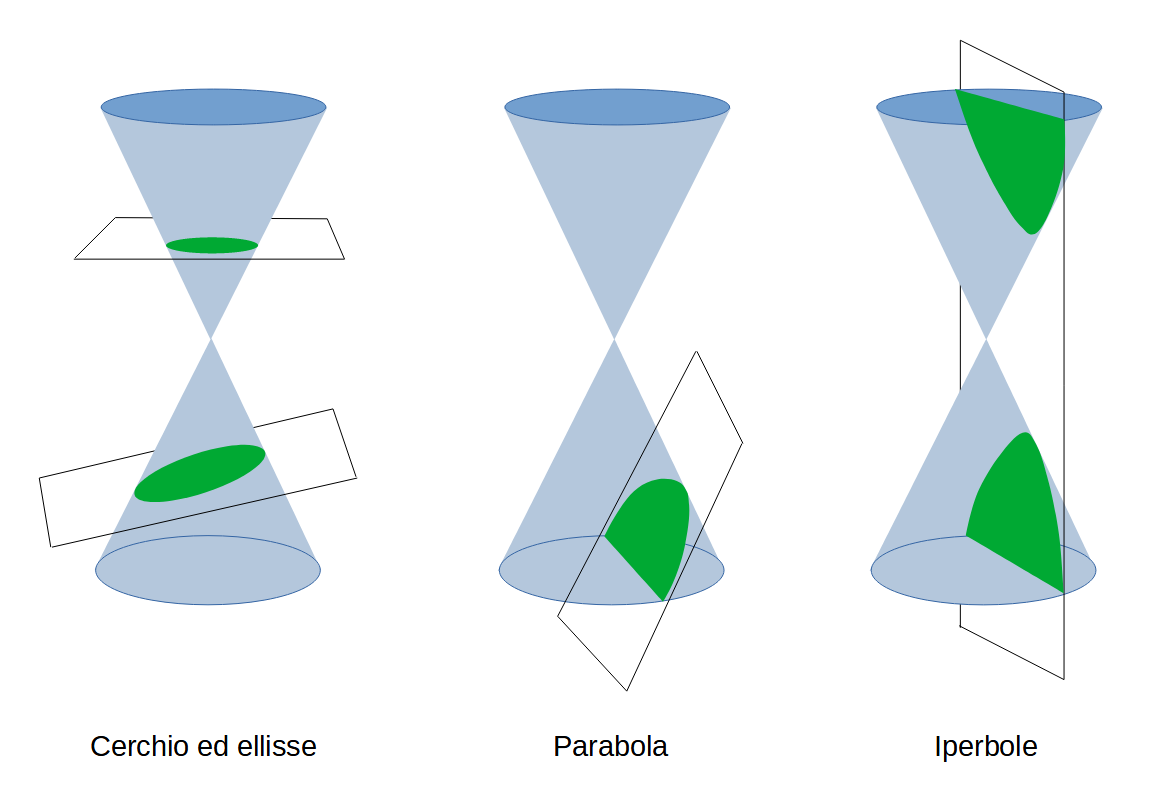
Le coniche
In geometria, l'intersezione della superficie di un cono con un piano genera una conica
Le coniche sono (con l'importanza per il corso di Matematica 1):
- La parabola (importantissima)
- Il cerchio (capita solo nelle diseq. con i numeri complessi o in Matematica 2)
- L'ellisse (poco importante)
- L'iperbole (interessa solo l'iperbole equilatera)
Le coniche
Le coniche sono curve non funzioni
- Le funzione associano ad una "x" una sola "y"
- Ad esempio, il cerchio è una curva e non una funzione perché ad un valore della "x" associa al più due valori della "y"
- Non va confuso il concetto di funzione con quello di equazione
In questo video parleremo della parabola
Parabola
La parabola ha equazione $$y=ax^2+bx+c$$
La parabola è anche una funzione
Non lo è la parabola con asse lungo l'asse "x" di equazione
$$ x = ay^2+by+c $$
Parabola: disegno
- intersezione con l'asse $y$, ovvero il punto $(0,c)$;
- segno di $a$:
- se $a>0$ ha concavità verso l'alto $\smallsmile$
- se $a<0$ ha concavità verso il basso $\smallfrown$
- intersezioni con l'asse $x$, ovvero si risolve l'equazione $ax^2+bx+c=0$
- se $\Delta>0$ allora ci sono due intersezioni con l'asse $x$: $(x_1,0)$ e $(x_2,0)$
- se $\Delta=0$ allora c'è una sola intersezione con l'asse $x$: $(x_{1,2},0)$ e coincide con il vertice della parabola
- se $\Delta<0$ allora c'è nessuna intersezione con l'asse $x$
- se $a>0$ la parabola sta sopra l'asse $x$
- se $a<0$ la parabola sta sotto l'asse $x$
- vertice della parabola: calcolo dell'equazione con $x=-{b\over 2a}$ (capita poco)
Esempio 1
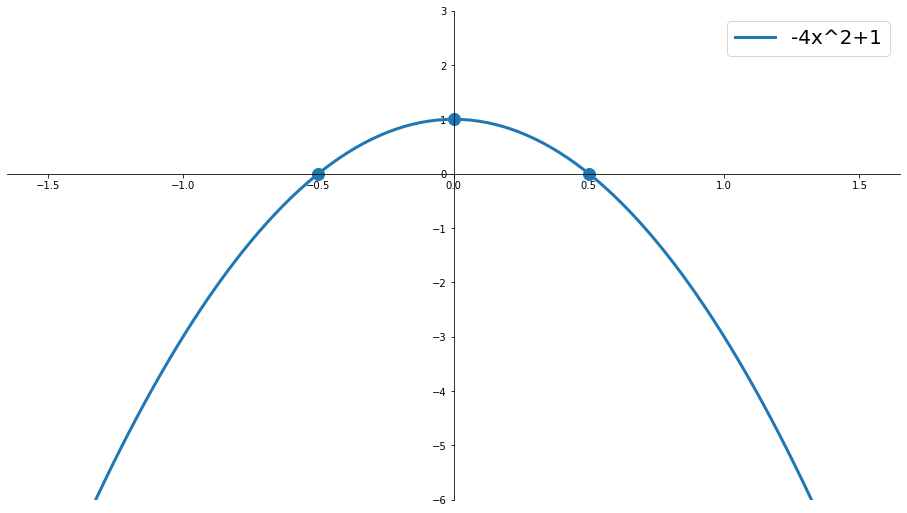
Disegnare la parabola $y=1-4x^2=-4x^2+1$
Soluzione
- per $x=0 \;\implies\; y=1 \;\implies\; (0,1)$
- $a=-4<0 \;\implies\; \smallfrown$
- $\Delta=0^2-4\cdot(-4)\cdot 1=16>0$ e quindi due radici reali: $$x_{1,2}={-0\pm\sqrt{16}\over 2\cdot(-4)}=\pm{1\over2}$$
Esempio 2
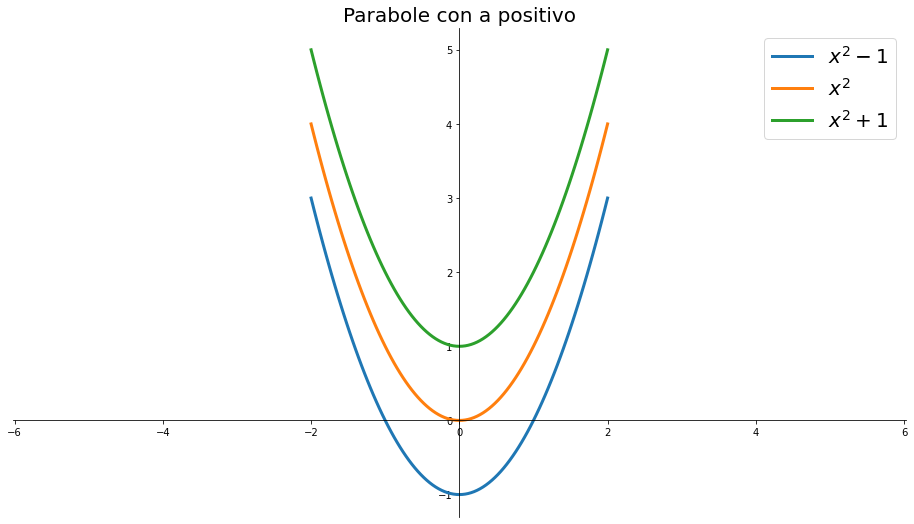
Rappresentare graficamente le seguenti parabole
- $y=x^2-1$
- $y=x^2$
- $y=x^2+1$
Soluzione
La seguente tabella riassume le caratteristiche delle parabole
| $y=x^2-1$ | $y=x^2$ | $y=x^2+1$ | |
|---|---|---|---|
| Segno di $a$ | $a>0$ | $a>0$ | $a>0$ |
| $\Delta$ | $\Delta=4>0$ | $\Delta=0$ | $\Delta=-4<0$ |
| N. radici | 2 radici reali | 1 radice reale | Nessuna radice reale |
| Radici | $x_{1,2}=\pm1$ | $x_{1,2}=0$ | --- |
Esempio 3
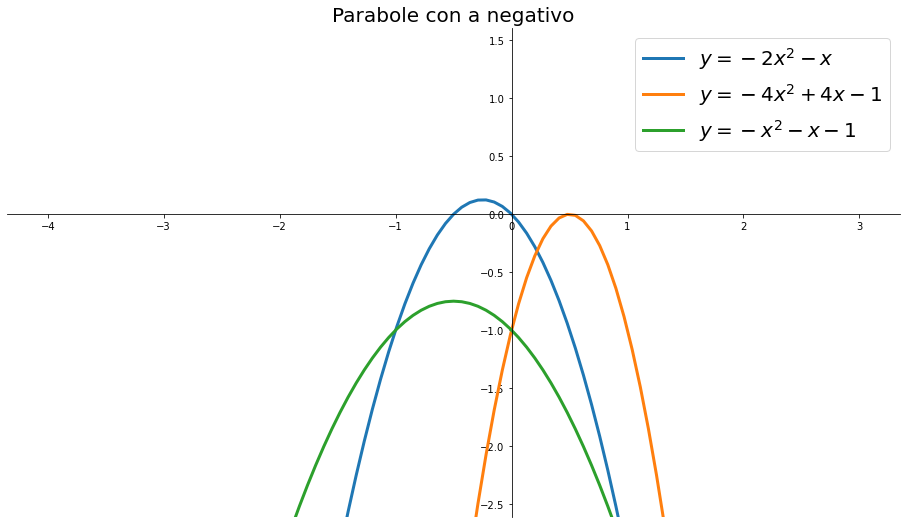
Rappresentare graficamente le seguenti parabole
- $y=-2x^2-x$
- $y=-4x^2+4x-1$
- $y=-x^2-x-1$
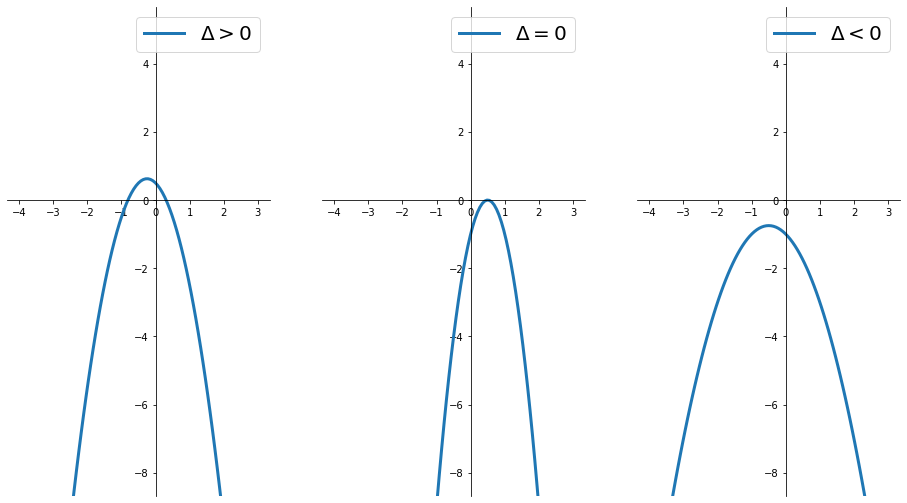
| $y=-2x^2-x$ | $y=-4x^2+4x-1$ | $y=-x^2-x-1$ | |
|---|---|---|---|
| Segno di $a$ | $a<0$ | $a<0$ | $a<0$ |
| $\Delta$ | $\Delta=1>0$ | $\Delta=0$ | $\Delta=-4<0$ |
| N. radici | 2 radici reali | 1 radice reale | Nessuna radice reale |
| Radici | $x_{1,2}=\left{0,\ -{1\over2}\right}$ | $x_{1,2}={1\over2}$ | --- |
Funzione positiva / zero / negativa
- Funzione positiva: per quali valori della "x" la funzione è positiva $f(x)>0$ ovvero sta sopra l'asse "x"
- Zero di funzione: per quali valori della "x" la funzione è zero $f(x)=0$ ovvero sta sull'asse "x"
- Funzione negativa: per quali valori della "x" la funzione è negativa $f(x)<0$ ovvero sta sotto l'asse "x"
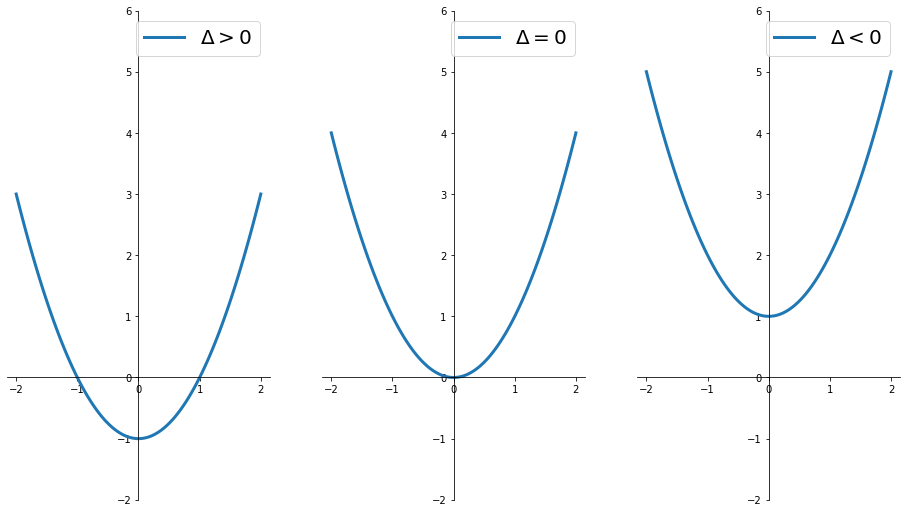
Segno con $a>0$
- $\Delta > 0$: è positiva per valori esterni alle radici
- $\Delta = 0$: è sempre maggiore o uguale a zero e vale zero nella radice / vertice
- $\Delta < 0$: è sempre strettamente maggiore di zero
Segno con $a<0$
- $\Delta > 0$: è positiva per valori interni alle radici
- $\Delta = 0$: è sempre minore o uguale a zero e vale zero nella radice / vertice
- $\Delta < 0$: è sempre strettamente minore di zero
Curiosità
Ricorda di sostenere questo progetto con una donazione (PayPal.Me/ManoloVenturin).
